Марат Авдыев - Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей

– Прочитайте, пожалуйста, Александр Николаевич, – обратилась она к Борщову, указывая на зеркало, где отражалось:

АД

– Ад! – прочитал Борщов, глядя в зеркало напротив столика.

– Представьте себе, что это слайды, – продолжала Татьяна. – Вы согласны, что происходит зеркальное отражение?

– Ну это очевидно! Но это почему мои собеседники читают все слайды нормально, а я – нет?

Татьяна жестом показала, что сейчас она всё объяснит и попросила Артура сесть напротив Борщова у свободного столика под зеркалом, держа в руках те же салфетки.

– Теперь снова ДА, прочитал Борщов.

– Александр Николаевич, – пришёл на помощь Матвей, – в мире программирования есть такая функция настройки дисплея, называется флип (flip) – отразить экран или фотографию. А вообще, программа может представлять изображение как угодно: прямо, зеркально, к верх ногами, под наклоном девяносто градусов и так далее. Но нам привычнее на экране читать тексты слева направо, а своё лицо видеть как в зеркале. Как бы Вы поступили на месте разработчиков зумпоподобных сервисов?

– Я бы… постарался сделать эффект полного присутствия – подумав немного ответил Борщов.

– Да, продолжила, Татьяна, поэтому свой текст на экране и своего собеседника мы видим без зеркального отражения, а изображение своей фигуры – как в зеркальном отражении. И всё что у нас за головой, попадающее в поле веб – камеры, мы также видим как в зеркале, посмотрите же на Артура ещё раз!

– Ах, да! – стукнул по своему столу Борщов. – ну какой я тупица! Это же надо, как просто! Коллеги, Вы меня положили на обе лопатки!

Ребята дружно улыбнулись, ещё бы: один гол в их пользу.

– Ну а теперь, я уверен, что с Теоремой Ферма Вы справитесь, – улыбаясь сказал Борщов. Что Вам удалось отыскать?

Матвей достал стопку листов с рисунками и стал пояснять. Он пытался разворачивать текст и рисунки к Борщову, но тот остановил репликой: я читаю вверх ногами без труда.

Матвей не торопясь начал:

– Давайте рассмотрим терему Ферма с позиции физики и геометрии. Именно в этом направлении есть шансы отыскать решение, основные идеи которого можно схематично уместить на достаточно широких полях книги.

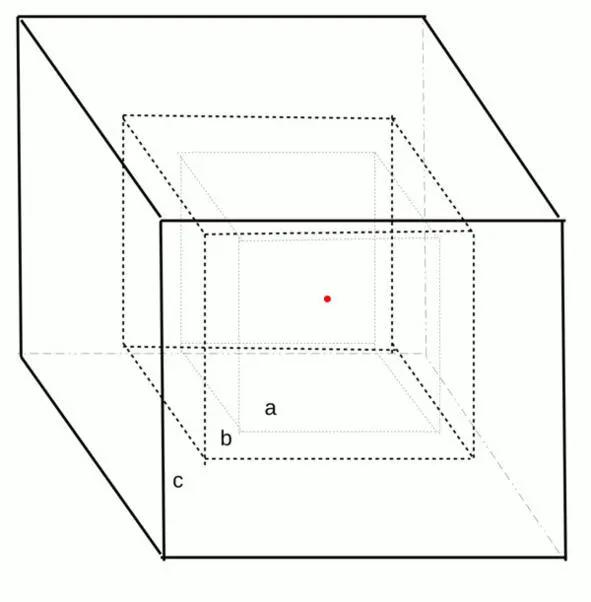
Рис. 2.1. Гиперкубы с ребрами a, b и c, вписанные друг в друга с общим центром, совпадающим с началом координат в пространстве размерности 3.

Не меняя общности, можно считать что справедливо неравенство для нашей тройки чисел a

На деле оказывается, что таким делителем всегда будет двойка и её степени, а это означает, что исходное предложение относительно числителя и знаменателя оказались ошибочными: оба они чётные, делятся на два, а мы исходно предполагали, что p, q не имеют общих делителей, которые заранее сократили.

Матвей говорил, водя карандашом по рисунку:

– Предположим, что искомая тройка целых чисел существует. Можно сопоставить ей соответствующую фигуру в виде гиперкубов с ребрами a, b и c, вписанными друг в друга в многомерном пространстве.

….… … … … …… … … … …… … … ……

Артур закрыл глаза и вспомнил, как накануне вечером Татьяна пригласил его подойти к трильяжу – тройному зеркалу на тумбе. Мама несколько раз порывалась выбросить этот бабушкин антиквариат, но Татьяна отстояла: очень ей нравилось рассматривать свои наряды и прочёску с помощью главного основного и двух боковых поворачивающихся зеркал.

– Ух как вкусно пахнет! – сказал Артур, схватив с тумбочки изящную коробочку из под одеколона.

– Отдай! Я сюда пригласил тебя не для того, чтобы нюхать парфюм – быстро ответил Татьяна и разложила на столе приготовленные для эксперимента предметы. – Смотри что я буду делать внимательно, а лучше снимай на видео.

Татьяна развернула зеркала в одну линию и придвинула коробочку плотно к правому углу главного зеркала. А затем спросила:

– Сколько ты видишь здесь коробочек?

– Ну конечно, две.

– А теперь? – Татьяна повернула к себе под прямым углом правое малое зеркало.

– Теперь четыре – ответил Артур. – Ну это и дураку понятно. В чём фокус?

– Не перебивай и смотри дальше!

Татьяна достала из ящика стола еще одно небольшое зеркало размером с тетрадь и положила его под коробочку.

– Ну, а теперь сколько ты видишь здесь коробочек?

– Раз, два\, три… да их уже стало восемь! – ответил Артур. – Интересно!

– Дальше будет самое интересное, – остановила его Татьяна. – Теперь я утеплю нашу коробочку. С этими словами она достала из портфеля квадратные постеры, отсчитала три пачки по десять листочков и принялась ими аккуратно оклеивать переднюю, боковую и верхнюю грани коробочки.

– Ты как-то плохо утепляешь свой домик – улыбаясь заметил Артур. – у тебя остаются щели.

– Вижу. Сейчас дойдёт очередь и до них.

И Татьяна извлекла из коробка три спички, срезала ножницами серные головки, чтобы не мешали, слегка промазала спички клеем и прикрепила на рёбра утепляемого домика.

– Всё равно остаётся вот эта дырка! – заметил Артур, указав пальцем на верхнюю боковую вершину созданного домика.

– Всему своё черёд – спокойно ответил Татьяна, закрывая эту вершину кусочком красного пластилина размером со спичечную головку. – А теперь скажи, сколько вершин ты видишь?

– Настоящую? Одну.

– Да нет, я не то имела ввиду. Сколько всего вершин ты видишь, не важно настоящие или отражённые?

– Раз, два, три… ну конечно восемь – ответил Артур.

– Вот именно! Каждое зеркало удваивает реальные и отражённые предметы, словно они такие же реальные. Два умножить на два, умножить на два или 2 3 будет восемь.

– Само собой, а где обещанный фокус?

– Фокуса никто не обещал, но он всё-таки здесь есть – улыбаясь ответил Татьяна. – Заметь, всё что я делала с малой коробочкой повторялось в зеркальном отражении. Я оклеила всего три грани: верхнюю, левую боковую и обращенную к нам. И в результате все шесть граней нашей фигуры стали покрытыми. Я прикрепила всего три спички по рёбрам домика – и в итоге все двенадцать рёбер нашего домика были закрыты. Наконец, я поместила кусочек пластилина в одну вершину – все восемь вершин оказались аккуратно зарытыми. Тем самым, мы покрыли нашу коробочку слоем . состоящим их трёх граней, трёх ребер и одной вершины.

– Экономно – задумчиво заметил Артур. Но что всё это значит?

– А это значит, что можно работать с тем представлением, которое нам удобно, но результат будет один. – назидательно сказала Татьяна. – Нам удобно описывать слой в представлении куба или гиперкуба «зажатого в угол» между зеркалами, так проще описывать его математическими формулами. В других ситуациях, нам важно заострить своё внимание на симметричности гиперкуба, совместив его центр с началом координат. Но оба представления легко преобразуются друг в друга. Ты всё аккуратно записал на видео?