Георгий Димитриади - Введение в финансовую математику

Различные процентные ставки

Процентная ставка рассматриваемого кредита может быть как фиксированной (постоянной), так и переменной, в зависимости от условий договора. Примером переменной ставки является ставка вида «LIBOR 1 1 Лондонская межбанковская ставка предложения ( англ. London Interbank Offered Rate, LIBOR) – средневзвешенная процентная ставка по межбанковским кредитам, предоставляемым банками, выступающими на лондонском межбанковском рынке с предложением средств в разных валютах и на разные сроки – от одного дня до 12 месяцев. Ставка фиксируется Британской Банковской Ассоциацией, начиная с 1985 года ежедневно в 11:00 по западноевропейскому времени на основании данных, предоставляемых избранными банками. + 1,5%». Ставки такого рода часто применяются на западных рынках. Произведем расчет наращенной суммы в случае переменной ставки.

Предположим, что ставка кредита меняется в течение его срока. Пусть полный срок кредита n разбит на периоды длины n 1, …, n k лет, причем в течение первого периода действовала процентная ставка i 1, в течение второго периода – i 2, …, в течение k -ого периода – i k .

Тогда в случае расчета по формуле простых процентов процентный доход за промежуток времени n 1будет:

I = in 1 P ,

…,

за промежуток времени n k :

I = in k P .

В итоге наращенная сумма составит:

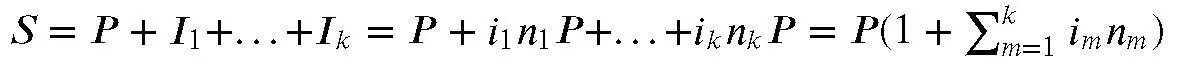
Из полученной формулы можно сделать следующие выводы. Размер наращенной суммы не зависит от порядка чередования периодов с различными процентными ставками. Кроме того, если в два или более периода имело место одна и та же процентная ставка, то для целей расчета наращенной суммы их можно объединить в один период, длительность которого равна сумме длительностей исходных.

Формулу можно переписать еще и так:

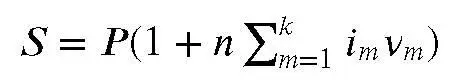
где ν m = n m / n – доля промежутка n m в полном сроке n рассматриваемого кредита. Получается, что для случая с переменной процентной ставкой можно ввести понятие эффективной процентной ставки простых процентов (см. об эффективных ставках подробнее ниже)

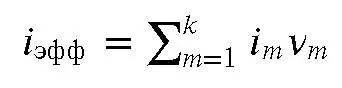
рассчитываемой как взвешенная сумма процентных ставок каждого периода. Эту ставку можно использовать как единый эквивалент для расчета наращенной суммы:

S = P (1 + i эфф n ).

Теперь перейдем к аналогичному расчету с использованием методики сложных процентов. По истечении первого периода n 1наращенная сумма составит:

.

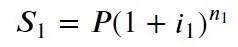
Поскольку сложные проценты начисляются на капитализированную сумму, после второго периода n 2наращенная сумма составит:

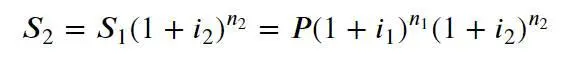
После k -ого периода n k найдем требуемую наращенную сумму:

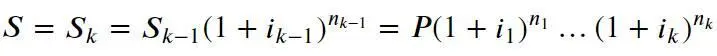
Из полученной формулы можно сделать следующие выводы, аналогичные тем, что были сделаны ранее для простых процентов: размер наращенной суммы не зависит от порядка чередования периодов с различными процентными ставками. Кроме того, если в два или более периода имело место одна и та же процентная ставка, то для целей расчета наращенной суммы их можно объединить в один, длительность которого равна сумме длительностей исходных промежутков.

Аналогично предыдущему можно ввести понятие эффективной ставки сложных процентов (см. подробнее об этом ниже):

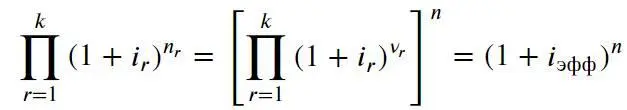
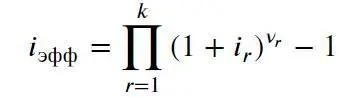
Здесь ν r = n r / n – доля промежутка n r в полном сроке рассматриваемого кредита. Получается, что для случая с переменной процентной ставкой можно ввести понятие эффективной процентной ставки сложных процентов, рассчитываемой как взвешенное произведение процентных ставок каждого периода, и которую можно использовать как единый эквивалент для расчета наращенной суммы:

S = P (1 + i эфф ) n .

Сложные проценты с начислением чаще, чем раз в год

Во всех рассуждениях ранее при использовании сложных процентов предполагалось, что они начисляются один раз в год. Однако на практике встречаются случаи, когда начисление происходит чаще. Пусть оно происходит m раз в год, где m – натуральное число. Например, начисление может происходить ежемесячно ( m = 12).

Для сложных процентов с начислением один раз в год была получена формула:

S = P (1 + i ) n .

Теперь мысленно предположим, что в рассуждениях, из которых была выведена эта формула, период времени «год» будет заменен на период времени «1/ m года» или « m -ая доля года». Поскольку все рассуждения останутся в силе, получим формулу:

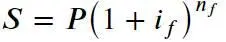
где i f – процентная ставка за « m -ую часть года», n f – срок, отраженный в «m-ых частях года» (а не в годах, как ранее). Для того, чтобы вернуться к используемым ранее обозначениям выразим i f и n f через годовые переменные:

i f = i / m , n f = mn .

Последнее соотношение легко интерпретируемо: при сроке n лет количество периодов размером «1/ m года» равно mn .

Тогда с использованием годовой процентной ставки итоговую формулу расчета наращенной суммы с использованием сложных процентов с начислением m раз в год можно записать как:

S = P (1 + i / m ) mn .

Поскольку, как было выяснено, формула сложных процентов с начислением m раз в год верна и для нецелого числа лет n , то и полученная формула верна для нецелого n . Более того, можно показать, что она остается верной и для нецелого m .

Отметим, что всегда предполагается, что сложные проценты начисляются один раз в год, если не указано противное.

Дня того, чтобы продемонстрировать зависимость наращенной суммы от количества начислений m раз в год, сведем в Таблицы 2 и 3 результаты расчетов при Р = 100 руб. и ставке i = 10% в Таблице 2 и ставке i = 25% в Таблице 3.