Николай Бетенеков - Избранные главы курса Радиохимия

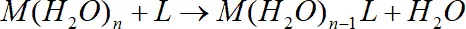, (1.1)

М – центральный ион, L – лиганд (органический или неорганический ион или нейтральная молекула), заряды для простоты опущены.

В процессе комплексообразования молекулы растворителя, окружающие центральный ион могут последовательно замещаться ионами или молекулами лиганда, что в итоге приводит к образованию комплекса ML n , где n – число лигандов в комплексе. Это число равно координационному числу, если лиганды образуют с центральным ионом только одну связь. Координационное число зависит от природы лиганда, поэтому к приписыванию данному центральному иону одного определенного координационного числа следует относиться с осторожностью. Классический подход к определению структуры координационных соединений заключался в том, чтобы установить структуру неизвестного соединения на основе структур известных изомеров. Структуры плоского квадрата, тетраэдра и октаэдра (рис. 1.2.), приписанные соединениям, были подтверждены физико-химическими методами. Хотя наиболее часто встречаются координационные числа 6 или 4, известны соединения, в которых центральный ион имеет координационное число вплоть до 10–12.

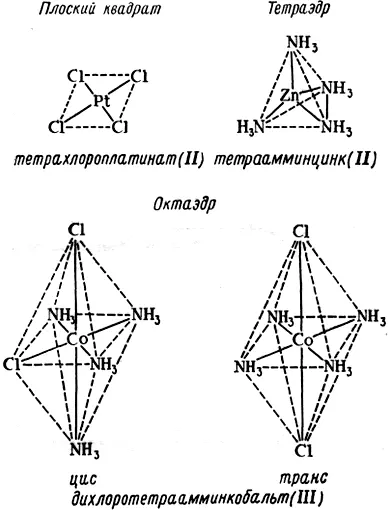
Рис. 1.2. Образование комплексов различной структуры [1].

В общем случае образование комплексного соединения можно выразить следующим уравнением:

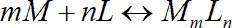, (1.2)

тогда термодинамическая константа комплексообразования:

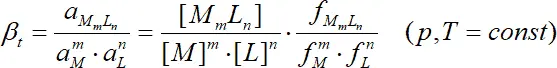, (1.3)

где a M = f [M] – активность, f – коэффициент активности, [ ] – символ концентрации. Согласно теории Дебая-Хюккеля, коэффициенты активности в разбавленных растворах в первом приближении определяются только ионной силой раствора и могут быть рассчитаны по уравнению Дэвиса [2].

При постоянной ионной силе J = const концентрационная константа β отличается от термодинамической константы β tпри J = 0 на постоянную величину, поэтому

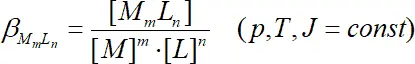. (1.4)

Если в структуре комплекса существует только один центральный атом, то он называется моноядерным, если m ≠ 1, то полиядерным. Хотя полиядерные комплексы встречаются также часто, как и моноядерные, в большинстве случаев их образованием пренебрегают, особенно при низких концентрациях.

Комплексы обычно образуются ступенчато, процесс характеризуется ступенчатыми константами комплексообразования K i:

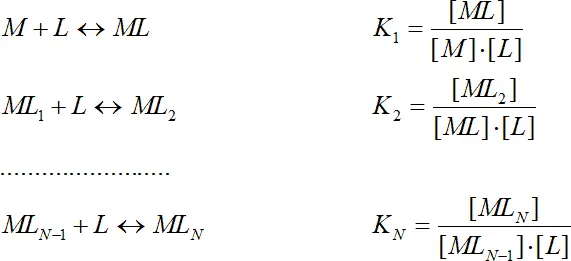(1.5)

Проведя подстановки: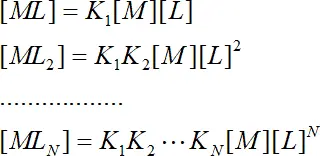

получаем 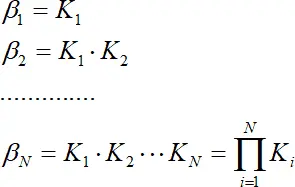, (1.6)

где β N – общая константа образования (устойчивости). В данном выражении N – число присоединенных лигандов, а не координационное число. Если рассматривать обратный процесс, то получаем реакцию диссоциации, которая характеризуется константой диссоциации или нестойкости k :

(1.7)

Константы нестойкости ступенчатые – обратные величины ступенчатым константам устойчивости. Общая константа нестойкости

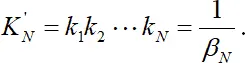. (1.8)

Для определения констант и описания форм состояния ионов в растворе имеют большое значение соотношения между константами и аналитически измеряемыми величинами. Общая концентрация металла в растворе в виде свободного иона и комплексных частиц определяется уравнением:

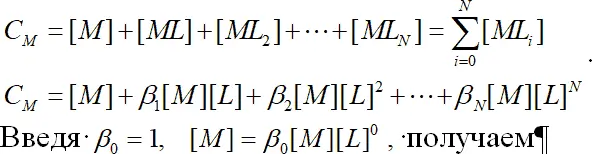. (1.9)

Введя 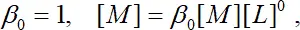получаем

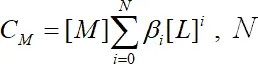N – максимальное число лигандов в комплексе.

Общую концентрацию лиганда можно определить:

(1.10)

Для определения степени закомплексованности Нильс Бьеррум предложил использовать среднее координационное или лигандное число, которое при заданных концентрации лиганда и константах устойчивости комплекса характеризует глубину комплексообразования. Среднее лигандное число и дает число лигандов, связанных с одним ионом металла – комплексообразователя во всех типах комплексов, т.е

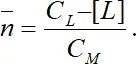
Подставив соответствующие выражения, получаем:

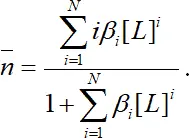(1.11)

При заданных β iсреднее лигандное число зависит только от концентрации лиганда и не зависит от концентрации металла в растворе (рис. 1.3). Это утверждение справедливо только для случая образования моноядерных комплексов. Если C L>>C M, то [L] ≈ C L. Когда C L<1 °C M, то при расчете нельзя пренебрегать связанным в комплекс лигандом.

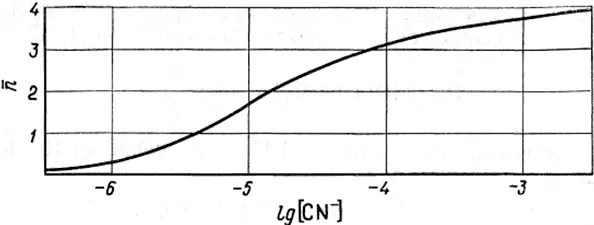
Рис. 1.3. Изменение среднего лигандного числа в зависимости от концентрации лиганда для цианидных комплексов кадмия [1].

Еще одна величина, которая нашла широкое применение, – это мольная доля i– комплекса в растворе α i.

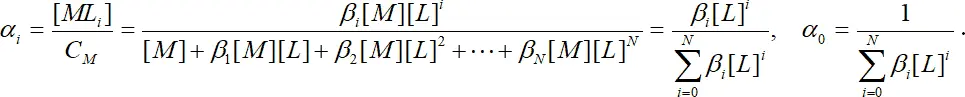. (1.12)

Из определения следует 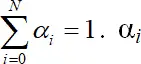α i зависят только от концентрации лиганда и не зависят от концентрации металла в растворе (рис. 1.4).