Сэм Лойд - Самые знаменитые головоломки мира

Квадрат диаметра пунктирного круга равен сумме квадратов двух найденных диаметров, то есть 242 + 242/49 – 12100/49. Извлекая отсюда квадратный корень, мы и находим искомую величину, равную 110/7 – 155/7 дюйма. Таков должен быть диаметр точильного круга, когда его получит второй компаньон.

15. Разумеется, выиграет кошка. Чтобы пробежать все расстояние и вернуться, ей нужно сделать ровно 100 прыжков. Собака, напротив, вынуждена проделать 102 фута и вернуться обратно. На своем 33-м прыжке она достигнет отметки 99 футов, и поэтому ей необходимо сделать еще один прыжок, который приведет ее на 2 фута дальше нужной отметки. Таким образом, чтобы пройти всю дистанцию, собака должна сделать 68 прыжков. Но частота ее прыжков составляет только 2/ 3от частоты прыжков кошки, так что на 100 прыжков кошки приходится лишь неполных 67 прыжков собаки.

Но у Барнума в кармане была возможность сыграть первоапрельскую шутку. Допустим, что кошку (а точнее, кота) зовут Васькой, а собаку – Жучкой! Тогда фразу «она делает 3 прыжка, в то время как ее соперник делает 2» следует понимать так, что собака пробегает расстояние в 9 футов, когда кот пробегает 4 фута. Таким образом, когда собака финиширует, сделав 68 прыжков, кот преодолеет расстояние всего лишь в 90 футов и 8 дюймов.

[Эта же самая головоломка вызвала в Лондоне чувство разочарования, когда Г. Э. Дьюдени опубликовал ее 1 апреля 1900 г. в еженедельнике The Weekly Dispatch. В варианте Дьюдени в беге состязались садовник (женщина) и повар (мужчина). – М. Г. ]

16. Ответ приведен на рисунке.

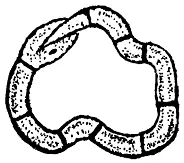
17. На эту задачу нет однозначного ответа, если только вы не знаете, сколько заплатил делец за свой велосипед первоначально. А раз в условии это не сказано, то и решить задачу удовлетворительным образом невозможно.

18. Бак с квадратным дном, ширина которого вдвое меньше глубины, имеет самые экономичные размеры. Если куб со стороной, близкой к 12,6 фута, вмещает 2000 кубических футов, то вдвое меньшая глубина приводит как раз к искомой 1000 кубических футов.

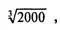
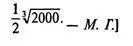
[Точные размеры искомого бака не выражаются в рациональных числах, поскольку они связаны с половиной «удвоенного куба». Если воспользоваться иррациональными числами, то длина и ширина искомого бака окажутсяравнымитогда как его высота составит

19. На рисунке искомая пятиконечная звезда окрашена целиком.

20. На рисунке показано, как можно разрезать греческий крест на пять частей, из которых удается сложить два креста одинаковых размеров. Проведите разрезы, как показано на кресте, изображенном слева, а затем сложите маленькие части, как показано на рисунке справа.

21. [Исходную головоломку решить невозможно, если не прибегнуть к мошенничеству, перевернув кубики с цифрами 6 и 9 вверх ногами. Одна из особенностей этой головоломки состоит в том, что любая подобная перестановка двух кубиков сразу же делает задачу разрешимой. Фактически любое нечетное число перестановок дает тот же самый эффект, тогда как любое их четное число оставляет, как и прежде, головоломку неразрешимой. Читателей, которых заинтересует математическая структура, лежащая в основе этой головоломки, мы отсылаем к классической работе W. W. Johnson, W. Е. Story. Notes on the 15-Pnzzle (American Journal of Mathematics, v. 2, 1879, p. 397), а также сборникам по занимательной математике. – M. Г. ]

Остальные три задачи решаются следующим образом.

Вторая задача. К расположению, указанному в условии, можно прийти за 44 хода: 14, 11, 12, 8, 7, 6, 10, 12, 8, 7, 4, 3, 6, 4, 7, 14, 11, 15, 13, 9, 12, 8, 4, 10, 8, 4, 14, 11, 15, 13, 9, 12, 4, 8, 5, 4, 8, 9, 13, 14, 10, 6, 2, 1.

Третья задача. К расположению, приведенному в условии, удается прийти за 39 ходов: 14, 15, 10, 6, 7, 11, 15, 10, 13, 9, 5, 1, 2, 3, 4, 8, 12, 15, 10, 13, 9, 5, 1, 2, 3, 4, 8, 12, 15, 14, 13, 9, 5, 1, 2, 3, 4, 8, 12.

Четвертая задача. Магический квадрат удается получить за 50 ходов: 12, 8, 4, 3, 2, 6, 10, 9, 13, 15, 14, 12, 8, 4, 7, 10, 9, 14, 12, 8, 4, 7, 10, 9, 6, 2, 3, 10, 9, 6, 5, 1, 2, 3, 6, 5, 3, 2, 1, 13, 14, 3, 2, 1, 13, 14, 3, 12, 15, 3.

22. Мэри Энн была матерью больного мальчика.

23. Если Ноббс может засадить борозду картошкой за 40 мин, то 6 борозд он засадит за 240 мин. Поскольку он засыпает картошку землей с той же скоростью, то он в состоянии полностью обработать 6 борозд за 480 мин, или за 8 ч. Хоббс, работая с другими шестью бороздами, засеет их за 120 мин (одну борозду – за 20 мин), а засыплет за 360 мин, что в сумме даст 480 мин, или 8 ч. Таким образом, проработав 8 ч, каждый из них сделает одинаковый объем работы; поэтому каждому из них следует получить по 2 доллара 50 центов.

24. Тайна золотого кирпича объясняется тем обстоятельством, что истинные размеры нового прямоугольника составляют не 23 × 25, а 23 × 25 1/23, дюйма, а это как раз и приводит к прежней площади в 5/6 квадратных дюймов.

[Относительно разнообразных «геометрических исчезновений» такого рода см. мою книгу «Mathematics Magic and Mistery» (Dover. Publ., 1956). – M. Г. ]

25. Согласно Евклиду, если две хорды пересекаются внутри круга, произведение длин частей одной из них равно произведению длин частей другой хорды. На рисунке поверхность воды образует хорду, а поскольку обе части этой хорды равны 21 дюйму, то их произведение равно 441.

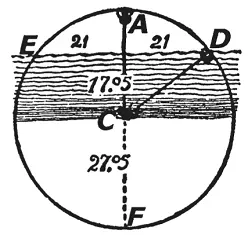
Прямая, проходящая вдоль стебля лилии, образует другую пересекающуюся хорду, у которой над водой возвышается участок в 10 дюймов. Произведение частей этой хорды тоже обязано равняться 441. Поэтому, разделив 441 на 10, мы находим, что длина второго участка этой хорды составляет 44,1 дюйма. Прибавив к этому значению 10 дюймов, мы находим, что длина всей хорды от А до F (диаметр круга) равна 54,1 дюйма. Значит, радиус круга равен 27,05 дюйма. Если мы вычтем отсюда 10 дюймов, то и найдем длину части стебля, находящейся под водой, то есть глубину озера; она составляет 17,05 дюйма.

26. Если вы проведете диагональ у прямоугольного листа бумаги, а затем свернете из этого листа цилиндр, то диагональ превратится в спираль, обвивающую цилиндр. Другими словами, спираль, обвивающую колонну, можно рассматривать как гипотенузу некоего прямоугольного треугольника. В данном случае это треугольник, который четыре раза оборачивается вокруг колонны. Основание этого треугольника в 4 раза больше длины окружности цилиндра (или в 4π раз больше его диаметра), что, как можно подсчитать, превышает 300 футов на пренебрежимо малую величину. Но этой же величине равна и высота башни, что является просто совпадением, поскольку высота вовсе на участвует в решении данной задачи.