Сэм Лойд - Самые знаменитые головоломки мира

37. Решения показаны на рисунках.

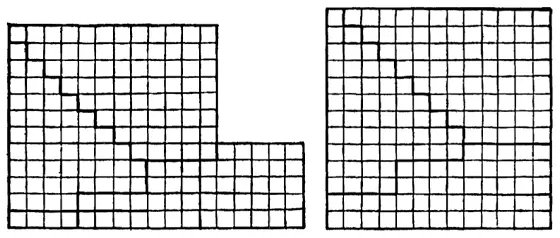
38. После замужества три невесты стали носить имена: Китти Браун, Нелли Джонс и Минни Робинсон, Китти весила 122, Нелли – 132, а Минни – 142 фунта.

39. Каждый камень в сережках весил 5 каратов, так что стоил он 2500 долларов, а цена обоих камней составляла 5000 долларов. Вес камней различной величины составил соответственно 1 карат (100 долларов) и 7 каратов (4900 долларов), а их суммарная стоимость также равна 5000 долларов.

40. В наилучшем решении требуется провести всего лишь два прямых разреза и перевернуть одну часть другой стороной кверху – прием, обычный в столярном деле, о котором не подумал ряд почитателей Евклида.

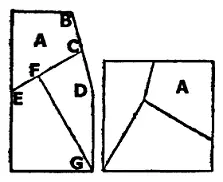
Не играет роли, если угол, образованный отрезком BD со стороной доски, окажется более или менее острым. Нужно просто провести прямую из середины левой стороны доски Е в середину BD. Затем следует опустить перпендикуляр из угла G на ЕС. Перевернув теперь часть А другой стороной кверху, можно сложить квадрат, как показано на рисунке.

41.

42. Разговор происходил в 9 ч 36 мин утра. Одна четверть времени, прошедшего с полуночи до момента разговора, равна 2 ч 24 мин, а половина времени от момента разговора до полуночи составляет 7 ч 12 мин; в сумме как раз и получается 9 ч 36 мин.

Если бы Мак-Гуир не пожелал Клэнси доброго утра (это указывает на то, что разговор происходил до полудня), то правильным ответом могло быть в равной мере и 7 ч. 12 мин. вечера.

43. Если минутная стрелка движется в 12 раз быстрее часовой, то они сливаются 11 раз в течение каждого 12-часового периода. Приняв одиннадцатую часть 12 ч за нашу основную константу, мы находим, что слияние стрелок будет происходить через каждые 65 5/11 мин, или через каждые 65 мин 27 3/11 с. Следовательно, в следующий раз стрелки сольются в 1 ч 5 мин и 27 3/11 с.

Ниже приведены моменты 11 слияний стрелок в течение каждого 12-часового периода.

12 ч 00 мин 00 с

1 ч 05 мин 27 3/11 с

2 ч 10 мин 54 6/11 с

3 ч 16 мин 21 9/11 с

4 ч 21 мин 49 1/11 с

5 ч 27 мин 16 4/11 с

6 ч 32 мин 43 7/11 с

7 ч 38 мин 10 10/11 с

8 ч 43 мин 38 2/11 с

9 ч 49 мин 05 5/11 с

10 ч 54 мин 32 8/11 с

[Теперь, когда вы освоились с техникой решения задач такого типа, вы можете попытаться решить следующую, по-видимому, более трудную головоломку. Предположим, что у часов – три стрелки, слившиеся в полдень. Третья стрелка, конечно, секундная. Когда в следующий раз сольются три стрелки?

На самом деле с помощью приведенной выше таблицы и некоторой проницательности задача решается гораздо легче, чем может показаться на первый взгляд. – М.Г. ]

44. Черные бумажные кусочки – это не более чем ловушка. Их следует сложить таким образом, чтобы в центре получилась маленькая белая лошадь, как показано на рисунке.

Именно этот трюк с белой апингтонской лошадью сделал популярным выражение: «О, но это же лошадь другой масти!»

45. Всего было три полностью слепых змея и три змея полностью зрячих.

46. Существует много простых способов выполнить задание за 15–18 ходов, но план, приведенный на рисунке, где мы возвращаемся в исходную точку через 14 ходов, кажется наилучшим возможным ответом.

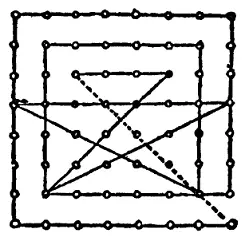
47. Решая задачу с ожерельем, всякий ювелир, так же как и 99 человек из 100, предложит распилить маленькие звенья на концах всех частей, что снизит цену всей работы до 1 доллара 80 центов. Однако правильным будет распилить все 10 звеньев в тех двух маленьких кусочках, которые состоят из пяти звеньев и содержат по 3 маленьких и 2 больших звена. Этими десятью звеньями можно соединить остальные части в замкнутое ожерелье. Стоимость всей работы окажется тогда равной 1 доллару 70 центам, что совпадает с наименьшим возможным ответом.

48. В головоломке с пастбищем необходимо учесть ежедневный прирост травы. Нам известно, что корова ест столько же, сколько коза и гусь. Следовательно, если корова и коза съедают всю траву да еще 45-дневный прирост за 45 дней, то ясно, что две козы и гусь съедят ту же траву за то же самое время. Поскольку коза и гусь съедают всю траву за вдвое большее время, мы видим, что одна коза съест всю траву за 90 дней и что гусь может питаться только приростом травы. Следовательно, если корова съедает 1/60 исходного запаса травы в день, а гусь 1/90, то вместе они съедят 1/36.Таким образом, корова и коза съедят первоначальный запас травы за 36 дней, а гусь в то же самое время позаботится об уничтожении ее прироста.

49. Ответ показан на рисунке.

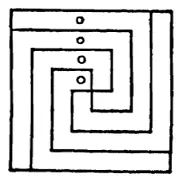
50. Миссис О'Тул весит 135, ребенок – 25, а собака – 10 фунтов.

51. Ответ ясен из рисунка.

52. Старую задачу, где требуется отмерить четыре кварты 5– и 3-квартовым кувшинами, можно решить за 6 операций:

1) наполните большой кувшин;

2) наполните маленький кувшин из большого, оставив в большом кувшине 2 кварты;

3) вылейте содержимое малого кувшина назад в бочку;

4) перелейте 2 кварты в маленький кувшин;

5) наполните большой кувшин из бочки;

6) наполните маленький кувшин из большого, причем в большом кувшине останется 4 кварты.

Что касается второй задачи, то с помощью элементарной алгебры мы находим, что при заданных ценах 26 галлонов «Утренней росы» должны содержать 24 8/17 галлона яблочной водки и 1 9/17 галлона сидра на общую сумму в 21,06 доллара. Чтобы получить такую смесь наискорейшим образом, необходимо предпринять следующее:

1) наполнить обе меры яблочной водкой;

2) вылить водку из бочки в бочонок покупателя;

3) вылить содержимое обеих мер обратно в бочку для яблочной водки;

4) перелить 2 галлона из бочонка в бочку с водкой;

5) перелить 2 галлона сидра из бочки с сидром в бочонок;

6) наполнить обе меры смесью из бочонка; при этом смесь, оставшаяся в бочонке, будет содержать 1 9/17 галлона сидра;

7) наполнить бочонок из бочки с яблочной водкой.

53. Существует бесконечно много пар чисел, сумма которых совпадает с их произведением. Если одно из этих чисел равно а, то второе получается с помощью деления а на а – 1. Например, 3 х 1 1/2 = 4 1/2 и 3 + + 1 1/2 = 4 1/2.