Сэм Лойд - Самые знаменитые головоломки мира

Далее, поскольку 3 1/8 цента составляют ровно 1/801 часть от 25,03125 доллара, то мы должны уменьшить 187,5 доллара на 1/801 часть этой суммы, что даст 187,27 доллара. Поэтому он получил жульнический доход в 25 долларов и 0,0006 цента. Ради еще большей точности я бы предположил, что продавцу шерсти перекупщик заплатил 187,2659176029973125 доллара минус 2 % комиссионных, или 3,745 доллара.

81. Раскусить этот старый орешек не удастся, если не знать, что в Англии и США для измерения веса большинства товаров используется коммерческая система мер, тогда как при взвешивании драгоценных металлов там пользуются тройской системой. Поэтому вес перьев определяется по первой, а вес золота – по второй системе.

Иногда считают, что в обеих системах фунт весит одинаково, но в коммерческой системе он делится на 16 унций, а в тройской – на 12, а иногда полагают, что при переходе от одной системы к другой не меняется унция, зато фунт в коммерческой системе весит 16 унций, а в тройской – только 12. Ни то, ни другое не верно. Истина состоит в том, что 1 фунт в коммерческой системе весит 7000 гранов, а в тройской – только 5760 гранов. [28]

Таким образом, шесть дюжин дюжин фунтов перьев в коммерческой системе весят 864 фунта, а полдюжины дюжин, или 72 фунта, в тройской системе при переводе в коммерческую систему составляют лишь 59 фунтов 3 унции и 407,5 грана. Поскольку 864 фунта равны 863 фунтам 15 унциям и 437,5 грана, то, вычитая отсюда 59 фунтов 3 унции и 407,5 грана, мы получим 804 фунта 12 унций и 30 гранов. Так выглядит ответ в коммерческой системе мер.

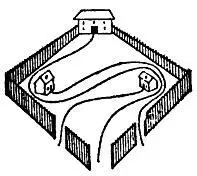
82. Сварливые соседи проложили свои дорожки, как показано на рисунке.

83. У честного молочника вначале было 5 галлонов молока в бидоне № 2 и 11 галлонов воды в бидоне № 1. В результате проведенных манипуляций в бидоне № 1 оказалось 6 галлонов воды и 2 галлона молока, а в бидоне № 2–5 галлонов воды и 3 галлона молока.

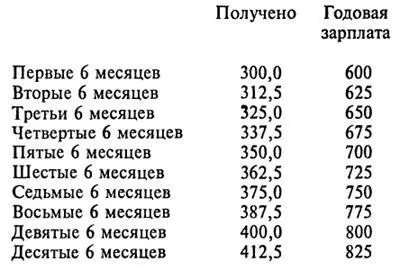
84. В первый год стенографистка выгадывает 12,5 доллара, но затем неуклонно теряет некую сумму. Иногда любители головоломок попадают в ловушку, добавляя всю прибавку к текущей сумме в конце каждых шести месяцев, в то время как годовая зарплата, возрастая каждый раз на 25 долларов, дает каждые 6 месяцев прибавку в 12,5 доллара. Разумеется, при ежегодном увеличении зарплаты на 100 долларов за 5 лет стенографистка получила бы 600 + 700 + 800 + 900 + 1000 = 4000 долларов. Вместо этого, согласно своему предложению, она за то же время получит на 437,5 доллара меньше, что видно из следующей таблицы:

85. Матери – 29 лет и 2 месяца, Томми – 5 лет и 10 месяцев, а его отцу – 35 лет.

86. Три дублета таковы: дважды стрелок попал в кольцо 25, дважды в кольцо 20 и дважды в кольцо 3.

87. Вот простой способ решения задачи, основанный на здравом смысле. Воспользовавшись движением вспять, применяемым при решении ряда головоломок, следует проанализировать последнюю выплату, определив, от какой суммы 1000 долларов составляют 105 %. Разделив 1000 на 105, мы устанавливаем, что последняя выплата состоит из 952,3809 доллара стоимости плюс 5 %.

Двигаясь назад, мы выясняем, от какой суммы 1952,3809 доллара составляют 105 %, и получаем 1859,4103 доллара. Добавляя новую выплату в 1000 долларов, мы получим, что предыдущая сумма составляла 2723,2479 доллара, а новое деление приводит к 3545,9503 доллара. Еще раз добавив 1000 долларов и вновь разделив их на 105, мы приходим к сумме 4329,4764 доллара, которая является исходной для вычисления процентов после первой выплаты в 1000 долларов. Таким образом, истинная стоимость покупки составляла 5329,4764 доллара, поскольку, начисляя от нее по 5 % годовых, мы и получим 6 выплат по 1000 долларов, как и оговаривалось в соглашении.

88. Задание можно выполнить за 19 шагов следующим образом: поднимитесь на перекладину 1, затем спуститесь снова на землю, а далее совершайте последовательно шаги на перекладине 1, 2, 3, 2, 3, 4, 5, 4, 5, 6, 7, 6, 7, 8, 9, 8, 9.

89. На рисунке к условию задачи изображены два грабителя, но не требуется быть Шерлоком Холмсом, чтобы понять, что грабителей было трое. Ведь требовалось разделить 21 пинту вина, 12 больших бутылок и 12 маленьких, а только 3 являются общим делителем этих чисел.

Один грабитель берет 3 полные кварты, 1 пустую кварту, 1 полную пинту и 3 пустые пинты. Каждый из двух оставшихся воров забирает 2 полные и 2 пустые кварты, 3 полные и 1 пустую пинты. Таким образом, каждый грабитель получает по 3,5 кварты вина и по 4 большие и 4 малые бутылки.

90. Сложите разницы в голосах с общим числом голосов и разделите на число кандидатов. Результат будет равен числу голосов, полученных победителем, откуда очевидным образом с помощью вычитания получатся и остальные числа. Таким образом, за кандидатов было подано соответственно 1336, 1314, 1306 и 1263 голоса.

91. Эта игра-головоломка дает широкий простор для неожиданных сюрпризов и красивых комбинаций. Первый игрок может выиграть 7 ячеек, соединив G с Н. Если второй игрок соединит J с К, топервый выиграет две ячейки, соединив К с О и Р с L, а затем сделает выжидающий ход от L к Я, вместо того чтобы выиграть еще 2 ячейки. Другой игрок выигрывает теперь 2 ячейки, соединив G с К, после чего он вынужден сделать еще один ход, который приносит первому игроку выигрыш остальных 5 ячеек.

Если после того, как первый игрок пойдет G – H, второй сделает ход D – Н, то первый ходит С – G, B – F, Е – F, a затем делает выжидающий ход M – N, врезультате чего ему обеспечен выигрыш еще четырех ячеек. Именно искусная тактика, когда жертвуют двумя ячейками, чтобы выиграть больше, придает особую пикантность этой игре.

[Эта головоломка, известная американским школьникам как «Точки и квадраты», являет собой самый простой пример топологической игры. Разумеется, в нее можно играть на прямоугольных полях различных размеров и форм. Квадратное поле с девятью точками проанализировать легко, но 16-точечная доска уже достаточно сложна. Мне не известны публикации, где бы анализировалась выигрышная стратегия первого или второго игрока (игра не может закончиться вничью, поскольку число нечетно).

В 1951 г. Ричард Хейнс придумал интересный трехмерный вариант этой игры, названный им «(Q-биклы». В эту игру можно играть также на двумерной решетке с треугольными или шестиугольными ячейками. – М. Г. ]

92. Геертринг купила 1 поросенка за 1 крону, а ее муж, которым обязан быть Корнелиус, купил 8 свиней по 8 крон каждая. Катрюн купила 9 свиней по 9 крон, а ее муж Клаас купил 12 свиней по 12 крон. Анна купила 31 борова по 31 кроне, а ее славный муж Хендрик купил 32 свиньи по 32 кроны каждая.

93. Чтобы решить задачу с минимальным числом частей, вначале отрежьте треугольники 7 и 2 и заполните ими выемку в центре. Сделав затем зигзагообразный разрез, передвиньте часть 4 на одну ступеньку вниз, в результате чего у вас получится правильный квадрат.