Сэм Лойд - Самые знаменитые головоломки мира

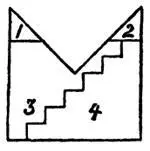
[По иронии судьбы, разделывая под орех «сообразительного Алека», С. Лойд сам допустил грубую ошибку. Как это подробно объяснил Генри Э. Дьюдени, [29]только прямоугольники определенных пропорций можно преобразовать в квадрат подобным ступенчатым способом.

В данном же случае стороны прямоугольника находятся в отношении 3:4, что не позволяет совершить нужное ступенчатое преобразование. Аккуратное решение с пятью частями дал Г. Э. Дьюдени. Решения с четырьмя частями до сих пор не было найдено.

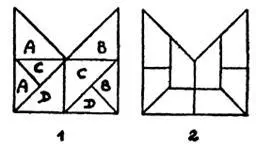
Даже старая задача Лойда, в которой лист бумаги, имеющий форму митры, требуется разрезать на четыре части одинаковых размеров и формы, решается лишь при неудовлетворительном допущении, что части, обозначенные одинаковыми буквами, соединяются в уголках и, следовательно, могут рассматриваться как одна часть! Лойд опубликовал также более приемлемое решение, содержащее 8 частей. – М. Г. ]

94. Задача решается с помощью ломаной из 14 звеньев, показанной на рисунке.

95. 1. Паровоз П (правый) отгоняет свои вагоны далеко вправо.

2. Паровоз П заходит в тупик.

3. Паровоз Л (левый) проезжает вместе с тремя вагонами вправо.

4. Паровоз П возвращается на основной путь.

5. Паровоз П перегоняет влево от тупика три вагона.

6. Паровоз Л заходит в тупик.

7. Паровоз П движется с вагонами вправо.

8. Паровоз П перегоняет 7 вагонов влево»

9. Паровоз Л возвращается на основной путь.

10. Паровоз Л возвращается к поезду.

11. Паровоз Л тянет 5 вагонов вправо от тупика.

12. Паровоз Л загоняет последний вагон в тупик.

13. Паровоз Л тянет 4 вагона вправо.

14. Паровоз Л толкает 4 вагона влево.

15. Паровоз Л один отъезжает вправо.

16. Паровоз Л возвращается к тупику.

17. Паровоз Л выводит вагон из тупика на основной путь.

18. Паровоз Л возвращается влево.

19. Паровоз Л идет вперед с шестью вагонами.

20. Паровоз Л загоняет задний вагон в тупик.

21. Паровоз Л движется вправо с пятью вагонами.

22. Паровоз Л отгоняет 5 вагонов влево.

23. Паровоз Л движется вправо с одним вагоном.

24. Паровоз Л возвращается к тупику.

25. Паровоз Л движется вправо с двумя вагонами.

26. Паровоз Л возвращается влево от тупика.

27. Паровоз Л тянет 7 вагонов вправо от тупика.

28. Паровоз Л загоняет последний вагон в тупик.

29. Паровоз Л движется вправо с шестью вагонами.

30. Поезд П движется вправо.

31. Поезд П забирает свои 4 вагона и уезжает.

32. Поезд Л движется к тупику.

33. Поезд Л забирает свой третий вагон и бодро движется своим путем.

96. Задачу можно решить, изменив положение двух уток, как показано на рисунке. При этом получается 5 рядов по 4 утки в каждом, а в ягдташе оказывается одна утка.

97. Миссис Джонс была дочерью Смита и племянницей Брауна, так что всего было 4 человека. Вклад составил 100 долларов, израсходовано было 92 доллара, а каждый получил в конце месяца по 2 доллара.

98. Странные часы следующий раз покажут правильное время в 7 ч 5 мин 27 3/11 с.

[Лойд не объясняет, как он пришел к этому ответу, но мы не можем удержаться от того, чтобы не указать, сколь простой становится эта задача после того, как вы решите задачу 43. Допустим, что у заколдованных часов четыре стрелки: одна пара их движется правильно, а скорости движения в другой паре переставлены. В переставленной паре стрелки покажут правильное время только тогда, когда они совпадут с соответствующими стрелками правильной пары – часовая с часовой, а минутная с минутной. Поскольку одна пара стрелок переставлена, мы можем рассматривать две стрелки, показывающие 12, как часовую и минутную стрелки и поставить вопрос, когда эти две стрелки совпадут в следующий раз. А в этом как раз и состоял вопрос задачи 43, где ответом было 12 ч 45 мин 27 3/11 с Однако в данном случае это дает нам положение лишь заколдованной минутной стрелки.

Теперь обратим внимание на пару часовых стрелок, указывающих на 6. Ситуация здесь будет аналогичной. Поскольку одна из этих стрелок движется как минутная, две стрелки встретятся на таком же расстоянии после 6, на каком предыдущая пара встречается после 12. Отсюда и получается приведенный выше ответ. – М. Г. ]

99.Когда Смит впервые встретился со своей будущей женой, он был втрое старше ее, но в день, о котором шла речь, 29 февраля 1896 года, ей было столько же лет, сколько ему было в момент их первой встречи. Значит, в момент первой встречи Тому было 15 лет, а его возлюбленной – 5, так что 29 февраля 1896 года ей должно быть 15 лет, а ему – 25. Следовательно, когда ей исполнится 45 лет, ему будет 55, что в сумме как раз и составит 100 лет.

Однако кое-кто, определив, что Тому 29 февраля 1896 года было 25 лет, впал в ту же ошибку, что и сам Том, утверждая, что в следующем високосном 1900 году ему исполнится 29 лет. На самом же деле ввиду одной из особенностей календаря 1900 год не високосный. Следующим високосным оказывается 1904 год, когда Тому исполняется 33 года.

100. Ответ ясен из рисунка.

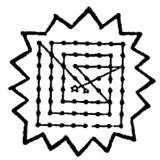
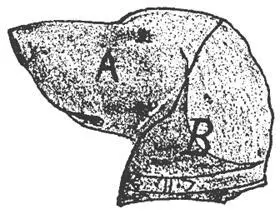
101. Полумесяц можно разрезать на 21 кусочек.

[Известно, что в случае круга с помощью п прямых разрезов можно получить максимум ( п 2+ п)/2 + 1 частей. Однако в случае полумесяца это число возрастает до ( п 2+ 3 п) /2+ 1. – М. Г. ]

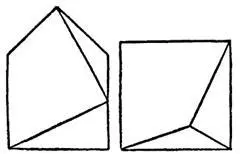
102. Ответ показан на рисунке.

103. Для того чтобы собрать 100 картофелин, необходимо преодолеть расстояние в 101 000 футов, или чуть больше 19 миль!

Для Гарри лучшая стратегия состоит в том, чтобы выбрать 99-ю картофелину. Том, бегая быстрее Гарри на 2,04 %, возьмет первую картофелину, Гарри – вторую, Том – третью и т. д. Однако Том бегает не настолько быстрее Гарри, чтобы забрать две соседние картофелины. Гарри потребуется преодолеть 49 980 футов, чтобы принести свои 49 картофелин. За то же самое время Том пробежит 50 999,592 фута, а поскольку для того, чтобы собрать все 50 картофелин, он должен покрыть расстояние в 51 000 футов, Гарри выиграет с преимуществом менее полуфута!

104. В этом простом примере «алгебры в картинках» мывстречаемся с фундаментальными принципами подстановки и добавления одинаковых величин в обе части равенства, не нарушающих, так сказать, равновесия. Это показывает справедливость аксиомы, что две какие-то величины, равные порознь третьей величине, равны и между собой.