Инесса Раскина - Логика для всех. От пиратов до мудрецов

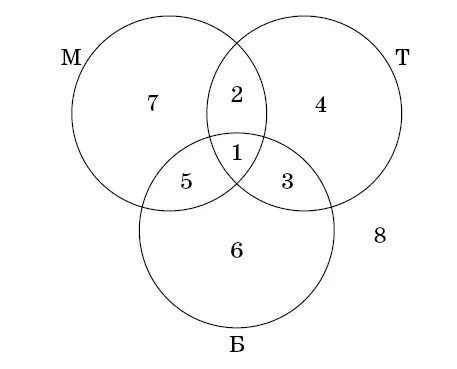
Рис. 24

Этому решению можно придать более наглядный вид (рис. 24). Вместо таинственных трехбуквенных кодов нарисуем три круга. В один поместим всех владельцев телевизоров, в другой – маляров, в третий – ежедневно посещающих бассейн. Людей, удовлетворяющих всем трем условиям, попросим разместиться на пересечении всех трех кругов, помеченном цифрой 1. Такие люди относятся к первой группе ТМБ. Люди из других групп тоже окажутся на территориях с прежними номерами. Восьмой группе предоставим территорию за пределами всех трех кругов. Дальнейшие рассуждения ничем не отличаются от предыдущей версии.

Ответ.Да, следует.

3.5. Прав, если считать, что марсиан не существует: ведь любое утверждение обо всех элементах пустого множества истинно.

3.6. 1) Нельзя, так как сумма масс 1 + 2 +… + 30 = 31 × 15 – нечетное число. 2) Можно. Пример можно построить, например, так. Сначала сформируем пятнадцать пар гирек веса 31: 1 + 30, 2 + 29 и т. д. Затем возьмем в каждую из трех куч по пять любых пар.

3.7. 1) Предположим, что таблицу заполнить удалось. Если найти сумму чисел во всех строках, то она окажется четным числом, а если во всех столбцах – то нечетным. Но это одно и то же число.

Ответ.Нельзя.

2) Для приведения примера достаточно заполнить первую строку двойками, а остальные – единицами. Заметим, что если заполнить квадрат 3x3 как попало, а остальные числа ставить в соответствии с условием, пример не может не получиться!

Ответ.Можно.

3.8. Нет. Контрпример изображен на рис. 25.

Рис. 25

3.9. Нет. Контрпример: 2 7+ 15 = 128 + 15 = 143 = 11 · 13.

Комментарий.В настоящее время неизвестно ни одной формулы для вычисления простых чисел.

3.10. Приведем несколько из многих возможных примеров:

1) 1111111212 делится на 12, 1111111125 делится на 15, 1111111432 делится на 16.

2) 111… 1151121792 делится на 128 (все пропущенные цифры – единицы), 222… 22399925 делится на 225 (все пропущенные цифры – двойки).

Ответ.Да.

Комментарий.Для проверки примеров достаточно выполнить деление в столбик. А придумать их можно с помощью признаков делимости: для делимости на 12 надо обеспечить делимость на 3 и 4, для делимости на 15 – на 3 и 5, на 225 – на 9 и 25. Но при сумме цифр 12 или 15 число заведомо кратно 3, а при сумме цифр 225 – кратно 9. Поэтому достаточно с помощью последних цифр обеспечить делимость соответственно на 4, 5 и 25, а затем лишь подобрать нужную сумму цифр. Кроме того, признаки делимости на 2 и 4 можно обобщить: число делится на n -ю степень двойки тогда и только тогда, когда на нее делится число, составленное из n последних цифр исходного. В частности, делимость на 16 проверяется по четырем последним цифрам, а на 128 – по семи. Остальные цифры многозначного числа выбираем любые, лишь бы сумма их была соответственно 16 или 128. Предлагаем читателю самостоятельно составить стозначное число с суммой цифр 144, делящееся на 144.

3.11.1) Высказывания Б, Г и Д равносильны. Они означают одно и то же: множества дедов и множество волшебников имеют хотя бы один общий элемент (см. рис. 26).

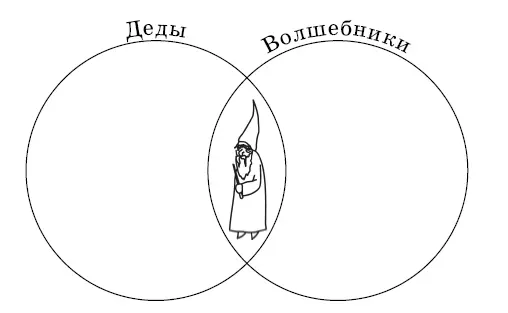
Рис. 26

2) Если А истинно, то истинны и высказывания Б, Г и Д (для них Дед Мороз является подтверждающим примером). А вот В может быть как истинным, так и ложным.

3.12. Подсказка.Верите ли вы вДеда Мороза?

Решение.Парадокс связан с различным пониманием высказывания «Дед Мороз – волшебник».

Первый вариант: существование Деда Мороза считается заранее известным, а в Б утверждается лишь, что он является волшебником. Тогда если верно В, то верно и Б, а если верно Б, то верно и А. В таком случае, действительно, если верно В, то верно и А, никакого контрпримера и противоречия здесь нет: раз мы договорились верить в существование Деда Мороза, то множество дедов не может быть пустым.

Второй вариант: заранее ничего не известно; в Б утверждается, что существует Дед Мороз, являющийся волшебником. Тогда если Б верно, то и А верно. Но утверждать, что если верно В, то верно и Б, нельзя (контрпримером является ситуация, когда множество дедов пусто), поэтому вывод «если верно В, то верно и А» делать тоже нельзя.

3.13. Обсуждение.Что останется, если убрать театрализацию? Утверждение «Если это утверждение истинно, то Дед Мороз существует». Истинно ли оно? Если да, то Дед Мороз существует. Но именно это в нем и сказано, то есть оно истинно. А раз оно истинно, то Дед Мороз существует.

Ответ.Проблема в том же месте, что и в задачах 1.4и 1.10первого занятия: классическая логика избегает утверждений, связанных с истинностью их самих: их нельзя считать ни истинными, ни ложными.

4.7. Пригласят.

Комментарий.Изобразим ситуацию с помощью кругов Эйлера (см. рис. 27). Начертим два пересекающихся круга. В первый круг пригласим тех, кто хорошо поет, во второй – всех, кто хорошо танцует. В ансамбль пригласят тех, кто оказался хотя бы в одном из кругов (на рисунке эта область выделена серым), в том числе и Наташу, находящуюся в пересечении кругов.

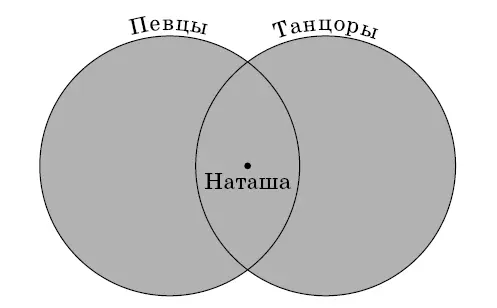
Рис. 27

4.8.Предположим, Сеня говорит правду. Тогда, согласно его словам, три остальных гнома – вруны. И, тем самым, фраза Бени является правдой. Значит, предположение приводит к противоречию, поэтому Сеня – врун, и его утверждение, что Женя – врун, является ложным. Отсюда заключаем, что Женя говорит правду. Тем самым, Беня – врун, а Веня говорит правду.

Замечание.Фраза Сени «Да оба они вруны» (относительно Бени и Вени) является ложной (несмотря на то, что Беня действительно врун), поскольку Веня – не врун.

Ответ.Женя и Веня.

4.9.Чтобы Аня и Боря были довольны, в пицце должен быть ровно один из ингредиентов: либо помидоры, либо грибы. С учетом вкусов Вани это должны быть грибы.

Ответ.С грибами.

4.10. Решение 1.Верна ровно одна из двух первых подсказок. Поэтому третья и четвертая неверны. Приз в желтом ящике.

Решение 2.Рассмотрим 4случая. Если приз в синем ящике, то верны подсказки 1и 4.Если в зеленом – то 1,3 и 4.Если в красном – то 2 и 4.Если в желтом – то только 2. Так как верна ровно одна подсказка, то приз находится в желтом ящике.

Ответ.Желтый.