Яков Перельман - Веселые задачи. Две сотни головоломок

122. При погружении в воду железная вещь (сплошная) теряет 8-ю долю своего веса [12] Я не сообщил этой цифры в условии задачи потому, что сама величина потери — 8-я, 10-я или 20-я часть — для решения задачи не имеет значения. . Поэтому и гири, и гвозди под водой будут иметь 7/ 8своего прежнего веса. И так как гири в 10 раз легче гвоздей, то и под водой они будут легче их в 10 раз. Следовательно, десятичные весы останутся и под водой в равновесии.

123. Из условия задачи мы знаем, что

вес бутылки + вес керосина = 1000 г.

А так как кислота вдвое тяжелее керосина, то вес бутылки + двойной вес керосина = 1600 г.

Отсюда ясно, что разница в весе: 1600–1000, т. е. 600 г, есть вес керосина, налитого в бутылку. Но бутылка вместе с керосином весит 1000 г; значит, бутылка весит 1000 — 600 = 400 г.

Действительно, вес кислоты (1600 — 400 = 1200 г) оказывается вдвое больше веса керосина.

124. Три четверти бруска мыла плюс гиря в 3/ 4килограмма весят столько же, сколько целый брусок. Но целый брусок — это 3/ 4бруска плюс 1/ 4бруска. Значит, 1/ 4бруска весит 3/ 4кг. И следовательно, целый брусок весит в четыре раза больше, чем 3/ 4 кг, т. е. 3 кг.

125. Сравнивая оба взвешивания, легко увидеть, что от замены одной кошки одним котенком вес груза уменьшился на 15–13, т. е. на 2 кг. Отсюда следует, что кошка тяжелее котенка на 2 кг. Зная это, заменим при первом взвешивании всех четырех кошек котятами: у нас будет тогда 4 + 3 = 7, а стрелка весов, вместо 15 кг, покажет на 2 × 4, т. е. на 8 кг меньше. Значит, 7 котят весят 15 — 8 = 7 кг.

Отсюда ясно, что котенок весит 1 кг, взрослая же кошка 1 + 2 = 3 кг.

126. Сравните первое и второе взвешивания. Вы видите, что раковину при первом взвешивании можно заменить 1 кубиком и 8 бусинами, потому что они имеют одинаковый вес. После такой замены у нас окажется на левой чашке 4 кубика и 8 бусин, которые будут уравновешиваться 12 бусинами. Сняв теперь с каждой чашки по 8 бусин, мы не нарушим равновесия; останется же у нас на левой чашке 4 кубика, на правой — 4 бусины. Значит, кубик и бусина весят одинаково.

Теперь определим, сколько бусин весит раковина: заменив (второе взвешивание) на правой чашке кубик бусиной, узнаем, что

вес раковины = весу 9 бусин.

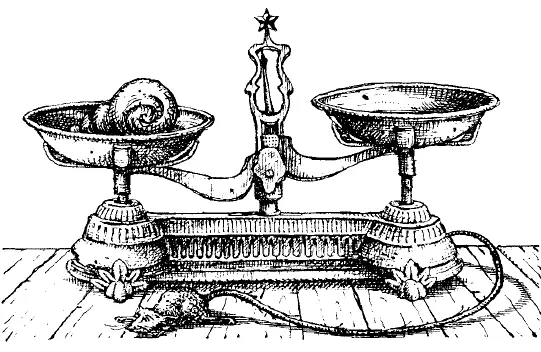
Рис. 133.

Полученный результат легко проверить: замените при первом взвешивании кубики и раковины на левой чашке соответственным числом бусин — получите 3 + 9 = 12 бусин, как и должно быть.

127. Заменим при первом взвешивании 1 грушу на 6 персиков и 1 яблочко: мы вправе это сделать, так как груша весит столько же, сколько 6 персиков и яблочко. У нас окажется на левой чашке 4 яблочка и 6 персиков, на правой — 10 персиков. Сняв с обеих чашек по 6 персиков, узнаем, что 4 яблочка весят столько, сколько весят 4 персика. Другими словами, один персик весит столько же, сколько одно яблочко. Теперь уже легко сообразить, что вес груши равен весу 7 персиков.

128. Эту задачу можно решить по-разному. Вот один из способов.

Заменим при третьем взвешивании каждый кувшин 1 бутылкой и 1 стаканом (из первого взвешивания следует, что весы при этом останутся в равновесии). Таким образом, 2 бутылки и 2 стакана уравновешиваются 3 блюдцами. На основании второго взвешивания, каждую бутылку мы можем заменить 1 стаканом и 1 блюдцем. Получив, что

4 стакана и 2 блюдца

уравновешиваются 3 блюдцами.

Сняв с каждой чашки весов по 2 блюдца, узнаем, что

4 стакана уравновешиваются

1 блюдцем.

И следовательно, бутылка уравновешивается (сравни со вторым взвешиванием) 5 стаканами.

129. Порядок отвешивания таков. На одну чашку кладут молоток, на другую — гирю и столько же сахарного песка, чтобы чашки уравновесились; ясно, что насыпанный на вторую чашку песок весит 900–500 = 400 г. Эту операцию выполняют еще три раза; остаток песка весит 2000 — (4 × 400) = 400 г. Теперь нужно содержимое каждого из пяти полученных 400-граммовых пакетов разделить пополам, на два равных по весу пакета. Делается это без гирь, очень просто: содержимое 400-граммового пакета рассыпают в два блюдца, поставленные на разные чашки, до тех пор, пока весы не уравновесятся.

130. Если бы заказанный венец был сделан из чистого золота, он весил бы вне воды 100 кг, а под водой терял 20-ю долю этого веса, т. е. полкилограмма. В действительности же венец, как мы знаем, теряет в воде не 1/ 2, а 10–9 1/ 4= 3/ 4 кг. Это происходит потому, что он содержит серебро — металл, теряющий в воде не 20-ю, а 10-ю долю своего веса. Значит, серебра в венце столько, что венец теряет в воде не 1/ 2 кг, а 3/ 4 кг — на 1/ 4 кг больше. Если в нашем чисто золотом венце мысленно заменить 1 кг золота серебром, то венец будет терять в воде на 1/ 10— 1/ 20= 1/ 20 кг больше, чем прежде. Следовательно, чтобы увеличить потерю веса на требуемую величину — 1/ 4 кг, необходимо заменить серебром столько килограммов золота, сколько раз 1/ 20 кг содержится в 1/ 4 кг. Поскольку 1/ 4: 1/ 20= 5, получаем: в венце вместо выданных 2 кг серебра и 8 кг золота 5 кг серебра и 5 кг золота. Три килограмма золота мастер заменил серебром и утаил.

Имеется квадратный пруд (рис. 134). По углам его, близ самой воды, растет 4 старых развесистых дуба. Пруд понадобилось расширить: сделать вдвое больше по площади, сохранив квадратную форму. Но вековые дубы трогать не хотят. Можно ли расширить пруд до требуемых размеров так, чтобы все 4 дуба, оставаясь на своих местах, оказались на берегах нового пруда?

Рис. 134. Задача о пруде.

Паркетчик вырезал квадраты из дерева и проверял свою работу, сравнивая длины их сторон. Если все четыре стороны были равны, то он считал квадрат вырезанным правильно.

Рис. 135.

Надежна ли такая проверка?

Другой паркетчик проверял свою работу иначе. Он мерил не стороны квадратов, а их диагонали (т. е. те косые линии, которые, перекрещиваясь, соединяют углы фигуры). Если обе диагонали оказывались равными, паркетчик считал квадрат вырезанным правильно.

Вы тоже думаете, что такая проверка правильна?

Третий паркетчик при проверке квадратов убеждался в том, что все 4 части, на которые диагонали разделяют друг друга (рис. 136), равны между собой. По его мнению, это доказывало, что вырезанный четырехугольник есть квадрат. Прав ли он?