Яков Перельман - Веселые задачи. Две сотни головоломок

Рис. 163.

Рис. 164.

На каждой вершине этой фигуры сходятся 4 ребра; в ней вовсе нет «нечетных» вершин.

Рис. 165.

Теперь перейдем к той задаче, которую решает наша муха: обойти по одному разу все ребра октаэдра, не отрывая пера от бумаги.

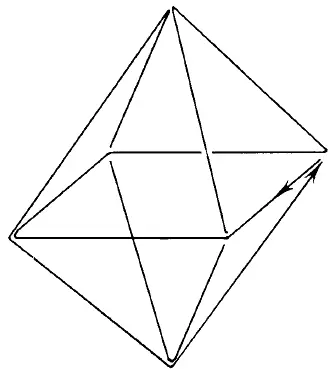
Рис. 166.

Поэтому можно начать путешествовать с любой вершины — вы обязательно возвратитесь в исходную точку. Вот одно из возможных решений (рис. 166).

— А знаете, это интересный род головоломок! Дайте мне десяток подобных задач, я подумаю о них на досуге.

— Извольте.

Рис. 167.

Рис. 168.

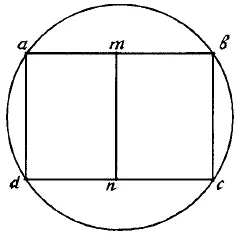
Рис. 169.

Рис. 170.

Рис. 171.

Рис. 172.

Рис. 173.

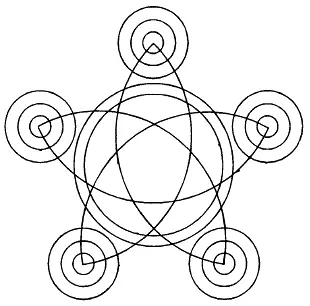
Рис. 174.

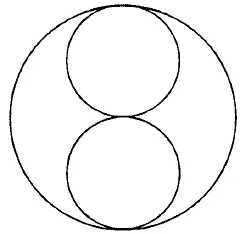
Рис. 175.

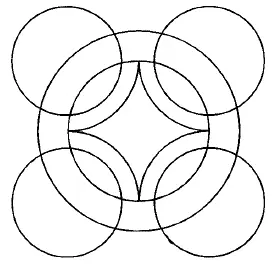
Рис. 176.

Из фигур, представленных на рис. 167–176, безусловно, можно начертить непрерывной линией фигуры с рис. 168, 170, 171, 172–176. В этих фигурах во всех точках пересечения сходится четное число линий, следовательно, каждая точка может быть начальной, она же будет и конечной. Выполнение фигур показано на рис. 177–185.

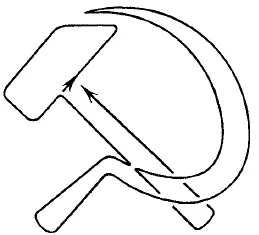
Рис. 177.

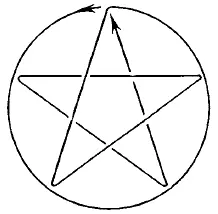
Рис. 178.

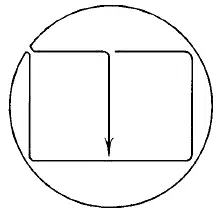
Рис. 179.

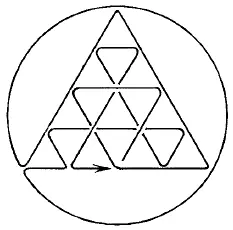
Рис. 180.

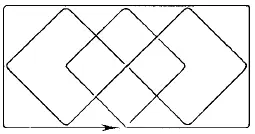
Рис. 181.

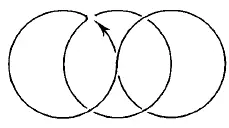
Рис. 182.

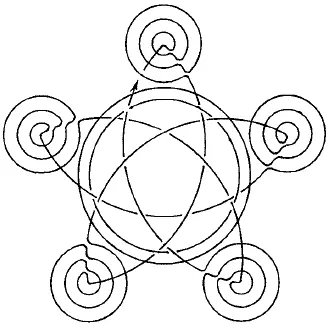
Рис. 183.

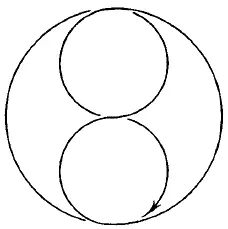
Рис. 184.

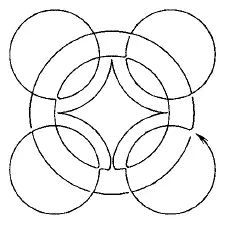
Рис. 185.

Фигура на рис. 167 имеет только две «нечетные» точки — те места, где ручка молотка входит в головку: в этих точках сходится по 3 линии. Поэтому фигуру можно начертить непрерывной линией только в том случае, если начать из одной «нечетной» точки и кончить в другой.

То же относится и к фигуре на рис. 169: она содержит только две «нечетные» точки, m и n . Они и будут начальной и конечной точкой при черчении.

Фигура на рис. 172. имеет более двух «нечетных» точек, а потому ее совершенно невозможно начертить одной непрерывной линией.

Часто приходится читать и слышать, будто одно из убедительных доказательств шарообразности Земли заключается в том, что линия горизонта повсюду имеет форму окружности, а коль скоро это так, отсюда делается вывод, что Земля наша должна быть шаром.

Подумайте, однако, какую форму имела бы линия горизонта, если бы Земля была не шарообразной, а плоской и бесконечно простиралась бы во все стороны?

«Уверяют, что Эзопова голова была длиной 7 дюймов, а ноги так длинны, как голова и половина туловища; туловище же равно длине ног с головою.

Спрашивается рост сего славного человека».

Вам, вероятно, знаком бессмысленный стишок:

Неведомый слагатель этих стихов стремился выразить ими заведомую нелепость и подбирал слова, которые противоречили бы одно другому.

Между тем приведенная фраза не совсем бессмысленна; на Земле существуют места, где такое определение времени применительно к некоторому реальному моменту вполне верно.

Где и когда это бывает?

Кузнецу принесли пять цепей, по три звена в каждой (рис. 186), и велели соединить их в одну цепь.

Рис. 186. Обрывки цепи.

Прежде чем приняться за дело, кузнец стал думать о том, сколько колец понадобится для этого раскрыть и вновь заковать. Он решил, что четыре.

Нельзя ли, однако, выполнить ту же работу, раскрыв меньше колец?

Нужно выразить число 16 с помощью 4 пятерок, соединяя их знаками арифметических действий. Как это сделать?

Мякоть вишни окружает ее косточку слоем толщиной в косточку. Будем считать, что и вишня, и косточка имеют форму шариков. Сообразите в уме, во сколько раз объем сочной части вишни больше объема косточки?

Продаются две дыни. Одна — окружность 72 см — стоит 40 рублей. Другая — окружность 60 см — стоит 25 рублей.

Какую дыню выгоднее купить?

В доске выпилены три отверстия: одно — квадратное, другое — круглое, третье — в форме креста (рис. 187). Нужно изготовить затычку такой формы, чтобы она годилась для всех этих отверстий.

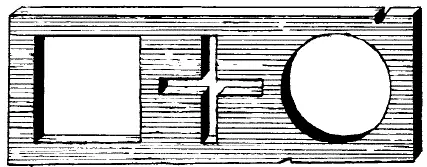
Рис. 187. Какой затычкой можно заткнуть все эти дыры?

Вам кажется, что такой затычки быть не может: отверстия чересчур разнообразны по форме. Могу вас уверить, что подобная затычка существует. Попытайтесь найти ее.