Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Ох, эта загадка, эта проблема озадачивает, манит, тревожит великие человеческие умы не одно столетие и даже тысячелетие по сей день.

Древнеегипетские жрецы (читай: учёные), пытаясь добраться до сердца этой тайны, нашли свой способ распрямления окружности с соблюдением точных линейных мер. Оказалось, что это возможно только в одном-единственном случае. 12-мерная окружность при этом превращалась в 12-мерный

п р я м о у г о л ь н ы й треугольник с точными мерами сторон: 3,4,5. – В общем, известный тебе египетский треугольник. Он и знаменовал собою круженье Времени (пространства-времени): год из 12 месяцев.

На какую мысль натолкнул этот эксперимент?

– Прямой угол(перпендикуляр) может стать ключом к исчислению круженья.

Древнегреческая мысль подхватила эту идею.

Пифагор оформил её в свою знаменитую теорему.

Новую проблему поставила гипотенуза. Её упрямая неточность для всех «неегипетских» случаев с прямоугольным треугольником.

В гипотенузе оказался кореньпроблемы. Она навсегда оказалась связанной с исчислением (извлечением) корня. А корень упрямо оказался связанным опять же с неточностью…

Выходило, что корень проблемы круженья – в линейной неточности.

А что же тогда т о ч н о?

Какими мерами т о ч н о можно измерить это самое круженье?

…Шумерские жрецы (читай: учёные) в поисках точности всматривались в звёздное небо.

У г л о в ы е меры!

Итак, наиболее точные меры для исчисления круженья – у г л о в ы е: у г л ы п о в о р о т а.

Вот что ещё интересно в связи с этим:

Учёные-кристаллографы (те, кто занимаются изучением мира кристаллов) тоже наиболее точными признают именно угловые меры, когда возникает необходимость определить вид минерала. Ведь внешне минералы – неправильной формы, разных размеров. А вот их кристаллические решётки (если изучить их изнутри) всегда неукоснительно соблюдают одни и те же углы в расположении атомов, характерные для определённых минералов.

А что удивительного? Ведь их формируют магнитные поля своим круженьем…

Для греков (в отличие от шумеров) был важен именно п р я м о й угол, перпендикуляр.

Он давал возможность создавать вещественныемодели космоса в земных условиях (архитектура). И вся их геометрия связана с прямым углом. Земля – космическое тело, и космос являет себя в земной жизни. И древнегреческие боги тоже ходили по земле, соединяя нашу планету и мир людей со Вселенной.

Слова «градус» древние греки ещё не употребляли. Они измеряли угловое круженье долями прямого угла!

Вот строчка из книги «Прометеева искра. Античные истоки искусства математики» А.В.Жукова :

«…углы Аристарх выражал не в градусах, а в д о л я х п р я м о г о у г л а».

(Аристарх Самосский – древнегреческий астроном, математик и философ III века до н.э., впервые предложивший гелиоцентрическую систему мира и разработавший научный метод определения расстояния до Солнца и Луны и их размеров.)

Вот! Слово «доля» – аналог, подобие «градуса»; прямой угол – подобие целого (360˚).

…А теперь так хочется быстренько пробежаться туда, в «Афинскую школу» (Рафаэля), где Боэций слушает Платона и конспектирует Пифагора, и ещё разочек заглянуть в его конспект и перечитать его новым озарённым умозрением!

Что там написано (по поводу октавы)?

… «Делить же он (Пифагор) начал следующим образом: прежде всего отнял от ц е л о г о одну д о л ю , затем вторую, вдвое большую, третью – в полтора раза больше второй и в три раза больше третьей, четвёртую – вдвое больше второй, пятую – втрое больше третьей, шестую – в восемь раз больше первой, а седьмую – больше первой в двадцать семь раз.»

Как-то уж очень похоже на то, что Пифагор пытался сопрячь, соединить звуковое круженье и угловое, чтобы у в и д е т ь (!) звуковую модель в своём умозрении.

Давай попробуем расписать этот текст как задачку.

«Доля» у нас неизвестное – икс х. Х может быть и звуковым интервалом, как прежде, и угловой мерой – если, как Пифагор, мы захотим у в и д е т ь звук как геометрию. Эти угловые меры мы можем обозначить привычными нам градусами вместо греческих «долей».

Рис. автора.

С седьмой доли начинается п о д о б и е. Подобие совокупности всех предыдущих.

В интервалах она даёт выход на лимму и подобие октавы в микроинтервалах, если помнишь.

А дальше – знакомые картинки.

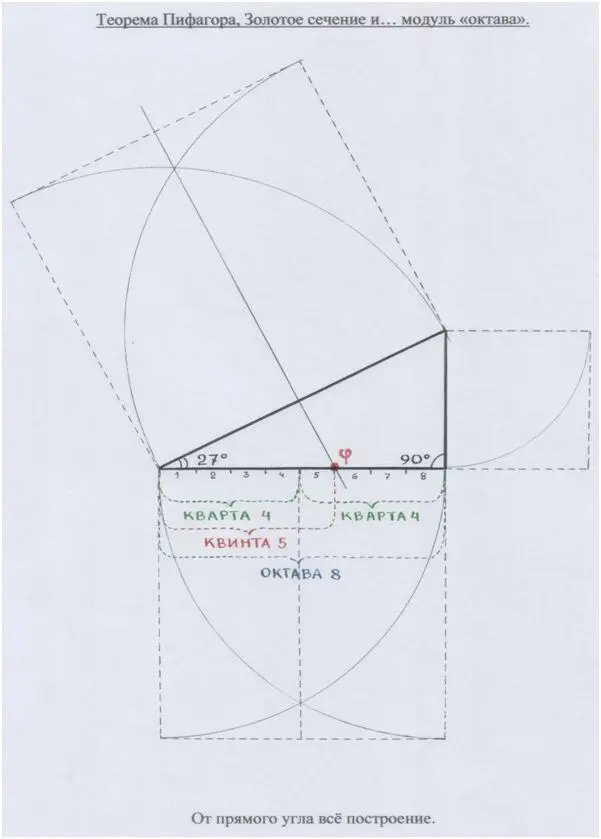
Рис. автора.

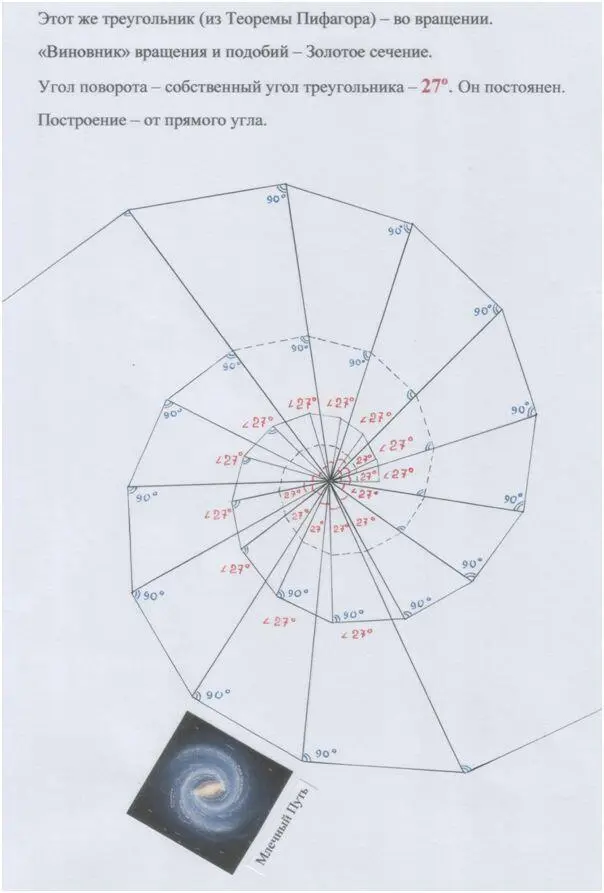
Рис. автора.

Рис. автора

Октава и её подобие, образующие «золотой» угол – 36º: как 36 звуков в пифагоровой октаве.

Постичь круженье, тем более измерить его – задачка, конечно, не из лёгких.

Перевести круг в треугольник – была замечательная идея египтян.

Сопряжение угловых поворотов и прямых линий впоследствии произвели на свет тригонометрические функции. Роль треугольника в измерении круженья оказалась неоценимой. Смысл понятия «тригонометрические функции»: «функция» – «роль», «дело»; «тригонон» (греч.) – «треугольник»; «метрео» (греч.) – «измеряю». Но нужно отметить, что с целочисленными результатами измерений здесь всегда проблема: ты знаешь, что значения синусов, косинусов, тангенсов, котангенсов – не целочисленны.

Да, всё то, что не прямолинейно, не хочет поддаваться простому, а зачастую и точному измерению. В состав формул для измерения круженья вообще входят б е с к о н е ч н ы е числа. Их называют т р а н с ц е н д е н т н ы м и: «транс» – «перенос». Эти числа переносятся через все пределы-границы, не знают конца.

Таких чисел три:

Знакомое тебе π, знакомое φ, и ещё е– число Эйлера, которое входит в состав натуральных логарифмов.

Все эти числа связаны с круженьем.

Тысячелетней давности задачка о квадратуре кругатоже оказалась связанной с бесконечностью и в результате – неразрешимой.

Но зато она в конце концов привела к очень даже современной идее

ф р а к т а л ь н о й г е о м е т р и и. А идея всё та же: ломать прямую на подобные кусочки-отрезки бесконечно и измерять их, измерять, измерять… Эти вычисления стали возможны только в век компьютеров.

Во все времена человеку хочется постичь и смоделировать мир, в котором он рождён.

У Пифагора не было компьютера. Но ему тоже хотелось моделировать.