Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Звуки кифары и в самом деле могут вызвать лёгкое кружение головы.

Они похожи на покачивающиеся в душистом тумане миражи. Такой туман поднимался из расселин дельфийских гор, и в этих испарениях жрицы солнечного Аполлона – пифии – провидели, прорицали будущее, судьбы людей, богов и мира. Слушая кифару, понимаешь, почему Пифагора звали Пифа-гор: прорицающий будущее на вершине – где небо дарит земле свой поцелуй.

Внимая звукам кифары, душа превращается в волны. И в этих волнах мерцают звёзды и плывут планеты…

Если пожелаешь увидеть это наяву, найди в Википедии статью «Луна». Там есть анимация: волнующаяся Луна. Взгляни – и внутри себя ты услышишь кифару.

Ты услышишь, наконец, загадочные неуловимые к о м м ы. Они послушны только кифаре, – потому что исполнить их можно лишь на этом удивительном инструменте. Специальные рожки и диски были изобретены греческими мастерами, чтобы музыкант мог чуткими движениями рук менять мгновенно едва-едва натяжение струн прямо во время исполнения. Какого же незаурядного исполнительского мастерства требовал этот божественный инструмент!

Учти, он может опьянить без вина…

В твоём Музыкальном энциклопедическом словаре должна быть статья про кифару. И в этой статье должно сообщаться о том, что от слова «кифара» произошли названия таких инструментов, как гитара и цитра. Когда какое-то слово пускается в странствие по Реке Времени, его звуки и буквы начинают колебаться, словно пифагоровы коммы. «К» может вибрировать, превращаясь то в «Г», то в «Ц»; «Ф» превращается в «Т». Если «К» превратится в «Ц», получится «цифара» – «цифра» (цитра-цифра).Забавно? Хотя, если знать, что струны кифары в ы ч и с л е н ы Пифагором, весь её строй основан на Ч и с л е, – то нет, не забавно, всё всерьёз.

Поющая математика!

Именно п о ю щ а я. Потому что кифара, по замыслу своих создателей (богов, не иначе, – пример с Гермесом), подражает г о л о с у. Она предназначена для исполнения м е л о д и и. Аккорды на кифаре не исполняют; изредка – благозвучные интервалы. Или – арпеджио (арфеджио – от «арфа»).О секундах и септимах речи быть не может! Это – д и с с о н а н с ы. А кифара – для прославления божественной г а р м о н и и, посредством к о н с о н а н с о в.

Вот когда секунды и септимы звучат не одновременно взятыми звуками, а перетекающими один в другой последовательно, получается льющаяся мелодия. Эти интервалы необходимы для с в я з и, и в этой роли они прекрасны! И совсем не противоречат гармонии.

Кроме того, предполагается, что «пение» этого инструмента – сольное.

С о л о. Подобно СОЛнцу, которое – о д н о. Кифара – голос Аполлона, бога Солнца.

Ты обратил внимание на то, что в древнегреческих росписях кифареды (исполнители на кифаре) – это боги, герои или крылатые музы? Личности космического масштаба!

Греки изображали их в окружении в о л н.

Странные волны. Прямоугольные.

Если помнишь, эти волны называют м е а н д р а м и.

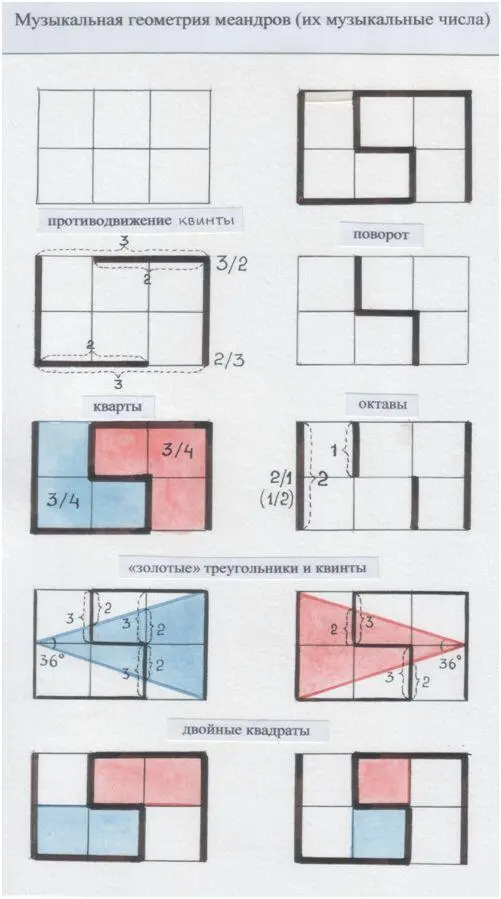
Рис. автора.

Рис. автора.

Две взаимно обратные спирали:

Рис. и модель автора

Рис. автора.

… и следы меандров в математике после античности – в картинках на следующих страницах:

Тебя уже осенили какие-нибудь догадки по поводу меандров?

?

Но почему же у греков эти меандры-волны, меандры-мелодии всё-таки

п р я м о у г о л ь н ы е?

Может быть, потому что для нас, живущих на поверхности Земли, так важен именно п е р п е н д и к у л я р. Он знаменует собою у с т о й ч и в о с т ь в этом зыбком, неостановимом, вращающемся космосе.

Но.

Ведь он запрятан – незримый! – внутрь Земли, Луны, Солнца, иных планет и звёзд, галактик, – как ось посреди экватора. Он запрятан внутрь кристаллов, растений, животных, нас самих. Он запрятан внутрь атомов, внутрь того, что само по себе незримо: внутрь электромагнитного поля. Ты, наверное, знаешь, что магнитное поле и электрическое – взаимно перпендикулярны.

Когда-то Ум человеческий сказал сам себе: возьму-ка я этот посох, чтобы дойти до самого сердца мира…

И что же стало?

Появилась линейка, появились меры, появились числа. Появились модели всего того, что познавал человек: архитектура, механизмы. Появилась механика Ньютона и система координат Декарта. Для чего? – Дабы познать само круженье в конце-то концов…

Сколько лет этому посоху познанья?

Древнегреческие меандры… В них – намёк. А от них в какую глубь и даль простирается путь?

Посмотрим?

Рис. и модель автора.

О пирамидах некоторые исследователи-египтологи пишут, что они имеют подобную наземной подземную часть. Может быть…

И если так, то это можно промоделировать знакомым тебе правильным многогранником, – одним из пяти, в которых находят золотую пропорцию.

Октаэдр! («окто» – «восемь», «эдр» – «грань»)

Это – о симметрии нашей планеты. Симметрии о к т а э д р а.

Вот куда нас завёл наш посох познания – перпендикуляр! – В самую сущность строения-строя Земли.

И Земля кружит в электромагнитном поле, где тоже действует перпендикуляр. Самый прочный на Земле кристалл – алмаз – сотворяясь глубоко в недрах земной коры, в своём строении воспроизводит действие этого поля и … повторяет симметрию Земли:

Так что меандры мы вполне можем вообразить развёрткой на плоскости нашей планеты – в геометрическом исполнении, конечно же.

Каким же образом это связано с о к т а в о й Пифагора?

Геометрически связано.

Через кварты! – «Кварта» – «четыре». Квадратное число. Квадрат.

Рис. и пометки автора.

Октава («восемь») – есть у д в о е н н а я кварта («четыре»).

Удвоение – признак г е о м е т р и ч е с к о й п р о г р е с с и и (k=2).

Кварты намекают нам на присутствие в музыкальном строе геометрической прогрессии.

Как ещё иначе проявляет себя геометрическая прогрессия в музыке?

Метрическим делением, нотными длительностями, градациями в р е м е н и звучания звуков.