Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

И тогда в этой микрооктаве ( размером в тон) между двумя лиммами (подобием двух кварт) образуется свой микротон (подобие т о н а) – комма.

Та самая комма, которая в настоящей октаве колеблется «между Солнцем и Луной».

Если к лиммеприбавить комму, получится апотома– подобие к в и н т ы в настоящей октаве.

Лимма+ комма= апотома

( Кварта+ тон= квинта)

Пифагор создал новую шкалу для октавы – из микроинтервалов, и наложил её на прежде полученную шкалу – из привычных нам интервалов.

Как это могло выглядеть?

Посмотрим…

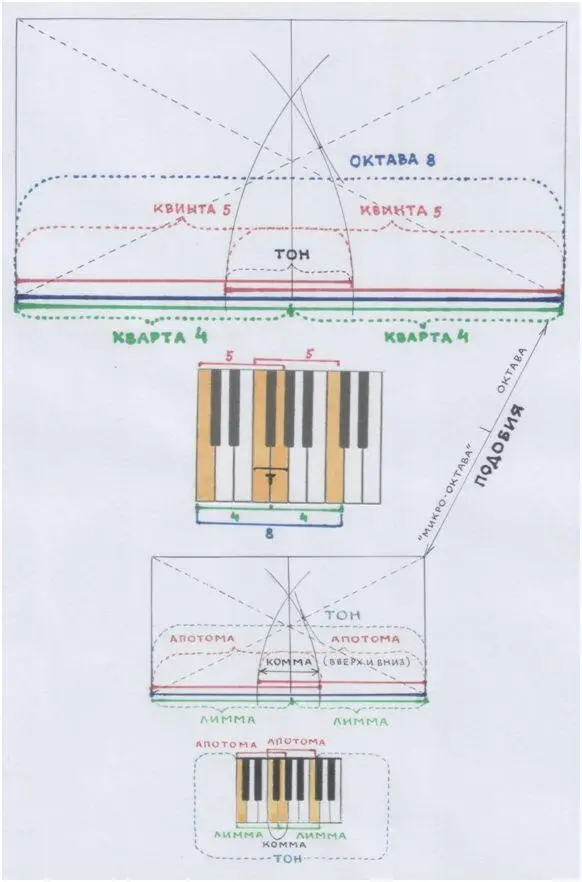
Рис. автора.

Если бы во времена Пифагора существовали клавиши, то мы, к своему изумлению, не обнаружили бы среди них привычных нам клавиш чёрных.

Почему?

Чёрные клавиши в том строе, которым мы пользуемся сейчас, показывают нам равномерно распределённые по октаве и чётко ф и к с и р о в а н н ы е половины тона – полутоны (лат. fixus– « прочный», « закреплённый»).

Полутон – самая маленькая мера этого знакомого нам строя. Дальше – ничего нет.

Как же это ничего нет?! – изумился бы, в свою очередь, Пифагор. – Разве космос так прост? Разве звуки конечны? Разве они так быстро и внезапно обрываются? Разве не летит их долгое эхо ( подобия-подобия-подобия…) в необъятные космические просторы?

В общем, при таком подходе, при таком м ы ш л е н и и о з в у к е, оборвать всё, как говорится, на полуслове – на полутоне – было немыслимо. Полутон не мог быть последней, конечной единицей измерения звукового пространства (пространства-времени на самом деле).

Если бы мы затеялись изобразить (начертить) подходящую клавиатуру, то в первом приближении она бы состояла только из белых клавиш. Она годилась бы только для до-мажора и ля-минора.

Из этого обычно и делается вывод, что первые музыкальные инструменты, начиная с древних шумерских арф, были пригодны для игры в до-мажоре и ля-миноре. Хотя, мы-то уже знаем, что никаких до-мажора и ля-минора тогда не было и в помине.

И всё же, на знакомой нам таблице мы видим что-то очень похожее на до-мажор. Да, нам так удобнее делать перевод с пифагорова музыкального языка на тот, что привычнее.

Мы сначала напомним себе таблицу, а потом будем следить за её преображением – вслед за мыслью Пифагора.

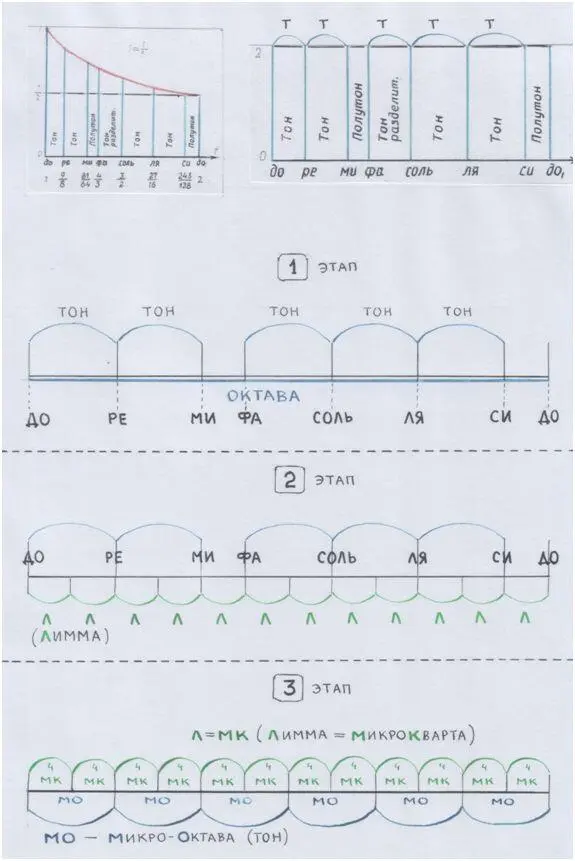
Рис. автора.

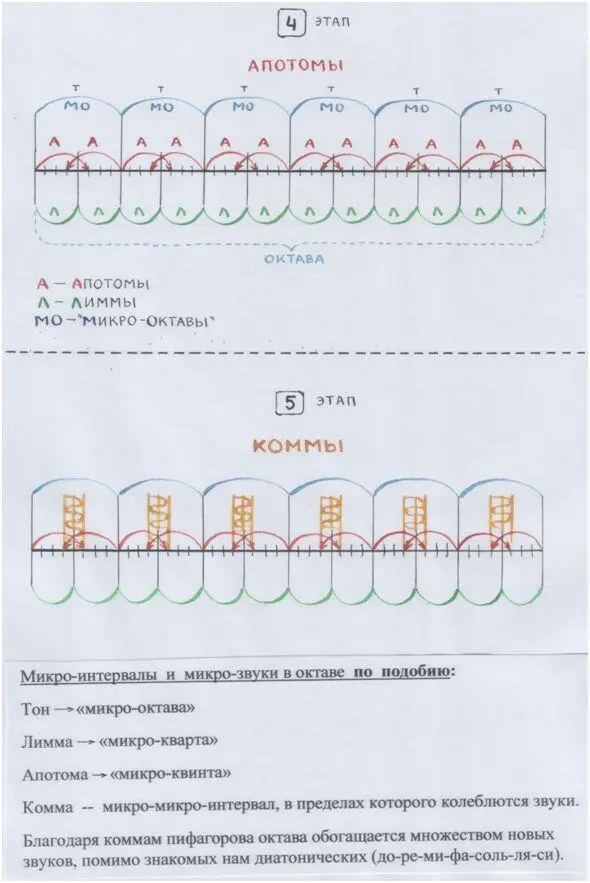
Рис. автора.

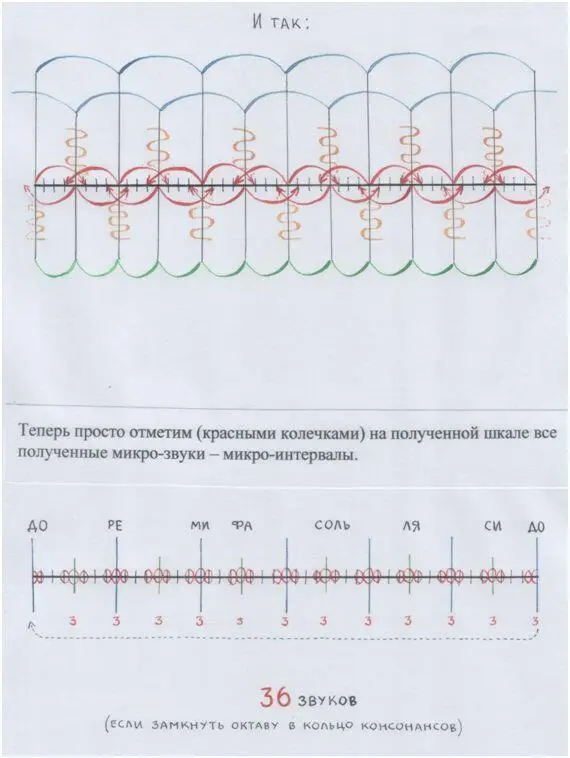
Рис. автора

Мы видим, что каждый знакомый нам звук октавы (гаммы) оказался в окружении микрозвуков, – словно он проверяет свою устойчивость, колеблясь между звуками вокруг него. И, благодаря этим звукам по соседству, он обретает объёмное, пространственное звучание. Так в воде растекается акварель. Так в компьютерной музыке моделируется звуковое эхо – из звуковых отражений-подобий.

Если мы затеемся и дальше делить коммы-интервалы, которые внутри октавы, – делить так же по принципу подобия, сначала надвое, – мы придём к шкале 72/72 (1/36 : 2 = 1/72) и получим знакомую нам комму, играющую важную роль в регулировании высоты звуков.

Звуки ведь не прекращаются (если их не остановить), они продолжают воспроизводить себя по подобию.

Ещё мы можем заметить, что звуки в пифагоровом строе распределяются неравномерно: сгущаются (вокруг главных, опорных, звуков: ДО_РЕ_МИ_ФА_СОЛЬ_ЛЯ_СИ_), будто стягиваемые магнитом, и – разрежаются.

Они ведут себя совершенно так же, как и волны давления воздуха на наши уши – те самые волны, которые превращаются в электрические импульсы и которые наш мозг кодирует затем в звуки.

Или – пружина ( модель звуковой ) волны: сгущения-разрежения…

Музыкальный строй Пифагора моделирует саму звуковую волну, её принцип! Восхитительно!

Как же тут, к слову, не вспомнить (опять!) о хорошо известном нам построении Золотого сечения. Ты помнишь, что творилось с гипотенузой под влиянием φ? Она, выходит, тоже вела себя звукоподобно: сжималась наподобие пружины и растягивалась-«разрежалась». А перпендикуляр едва удерживался, чтобы не колебаться вместе с нею. Он был в роли опоры – как опорный звук (до, ре, ми… и т.д.).

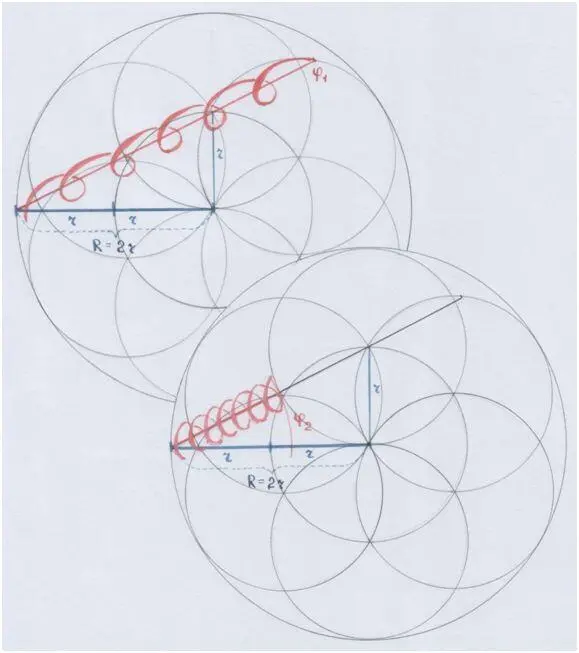
Рис. автора.

Вот чем ещё хорош образ пружины: он показывает в р а щ е н и е.

Оно уже наметилось в перекрёстах апотом:

Рис. автора.

И это – неспроста!

Следующая нам забава – та, что приготовил профессор Белявский. Она в его книге «Теория звука в приложении к музыке» в виде таблицы с математическими расчётами звуков.

Расчётами мы на сей раз заниматься не будем. Таблицу полностью ты найдёшь на стр.79, если любопытство покою не даст.

А я сейчас просто аккуратно выпишу п о с л е д о в а т е л ь н о с т ь звуков в музыкальном строе Пифагора по версии профессора.

Следи:

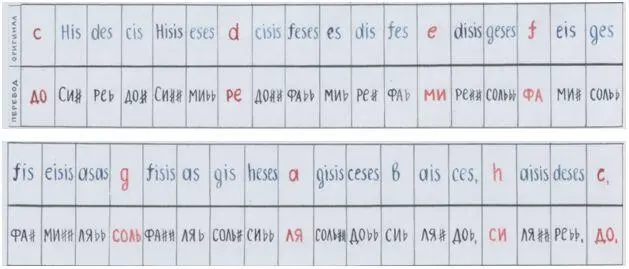
Рис. автора.

Ты когда-нибудь видел т а к о е?!

Ты такую последовательность когда-нибудь видел?

Лично я – нет. До встречи с этим почтенным профессором в названной книге.

Опорные звуки гаммы – да, на месте. А вот звуки между… Скачут, как зайцы – друг через друга, задом наперёд… Что это такое?

На фортепиано воспроизвести значительную часть этих звуков попросту невозможно, не пытайся. Не следует обольщаться внешней похожестью знаков альтерации на знакомые нам дубль-диезы, дубль-бемоли. В случае с пифагоровым строем – это всё условности, как впрочем, и обозначения нот (мы-то уж знаем). Все эти знаки – лишь подыскиваемые «слова»-эквиваленты: «вот это похоже на наш дважды диез», а это – «похоже на наш дважды бемоль». П о х о ж е. Не р а в н о, а – п о д о б н о. Для нас ## (дважды диез) означает подняться на полтона и ещё раз ровно на столько же.

В системе п о д о б и й это будет предполагать: подняться на полтона и ещё на часть полутона – на микроинтервал, например (комму, комму коммы…).

Что-то вроде этого: