Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Только в отношении звуковых волн Герц уточнил пифагорово «чуть-чуть». Например, интервал квинта определяется отношением частот не 1,5 или 1,499…(в переводе на десятичные дроби), а 1,498…

Может быть, потому что и сам солнечно-лунный календарь со времён Пифагора как-то уточнили… И поведение волн было более тщательно исследовано физиками: добавились параметры скорости, амплитуды, – всего того, что вносит коррективы в строгую зеркальную симметрию обычных дробей, выражающих обратность пропорций длин и частот волн : 2/1, 1/2;

3/2, 2/3; 4/3, 3/4 …

Рис. автора.

Из-за этих самых обычных дробей с их строго зеркальной симметрией Пифагора стало как-то принято (однако далеко не всеми теоретиками музыки, но всё-таки многими) «подозревать» в неточности. Но! Как-то забывается при этом о разработанной им с особой тщательностью системой настройки. Сторонники Пифагора как раз это учитывают.

Самое поразительное, что именно система настройки с помощью тех же самых простых дробей давала весьма точный результат на практике.

Если ты ещё не устал, давай-ка вспомним, из чего исходил Пифагор, обнаружив космическую связь между звуком и временем, временем и числом, числом и геометрией.

Идеальное годовое время Земли, её путь по окружности – 360˚. Это идеальное время/путь устанавливается как центр симметрии между солнечным годом на Земле в 365˚(дней) и лунным годом в 355˚(дней). + – 5˚, всего диапазон в 10˚(дней).

Рис. автора.

1/5 часть всей этой системы отношений воспроизводит в с ю эту систему, показывая те же самые отношения ( 1/5 от 360˚ – 72˚):

365/360 = 1, 0138888…. 73/72 = 1, 0138888…

360/365 = 0,9863013… 72/73 = 0,9863013…

360/355 = 1,0140845… 72/71 = 1,0140845…

355/360 = 0,9861111… 71/72 = 0,9861111…

Выходит, мы имеем дело с п о д о б и е м, и, какие бы операции мы ни совершали в этой 1/5 части всей системы, они будут отражением того, что происходит в ЦЕЛОМ. Система Солнце-Луна-Земля – ЦЕЛОЕ. 1/5 этого целого – система консонансов звуковых волн.

Диапазон 71-73 (с центром симметрии 72) в системе консонансов волн подобен диапазону «10» (365дней или градусов поворота минус 355 дней или градусов поворота, центр симметрии – 360 дней или градусов поворота) в космической системе.

Разница между отношениями 73/72 и 72/71 (как и между 365/360 и 360/355) равна: 1,0138888… – 1,0140845… ≈ – 0,0001957… ≈ – 0,0002

А теперь поступим опять же по подобию.

Как сама комма «набегает» из разницы в 0,0138888… в каждом делении шкалы волн (0,0138888… х 72 = 1,0138888…), так и в диапазоне «10» «набегает» своя микро-комма: – 0,0002 х 10 = – 0,002

То есть примерно в минус две тысячные: ≈ – 0,002

Это означает, что при настройке струн ( «по Луне») эта разница и учитывается и осуществляется.

Самым главным интервалом при настройке считается квинта. Наверное, ты уже догадываешься почему. – Это фундаментальный интервал, доминантный. «Первоинтервал», «кирпичик» (ещё говорят «краеугольный камень») музыкального строя.

Так вот, при настройке «по Луне» отношение 3/2, или 1,5 превращается в отношение 1,5 – 0,002.

Приблизительно, конечно, округлённо: ≈ 1,498…

…Когда Генрих Фердинанд Герц спустя почти 2,5 тысячелетия после Пифагора изобрёл свой герц, волны стали измерять этими самыми герцами. К а ж д ы й индивидуальный, особенный и неповторимый звук – в герцах. Но эти звуки-индивидуальности в музыкальном строе оказались верны тем

о б щ и м п р и н ц и п а м отношений между звуками, которые обнаружил первооткрыватель Пифагор.

Любопытно, очень любопытно взглянуть хотя бы на часть таблицы, где представлены звуки-индивидуальности с их неповторимым обликом/образом в герцах.

Если хочешь, поиграйся с отношениями между «индивидуалистами», взяв калькулятор.

Особенно интересно, как обстоит дело с квинтами.

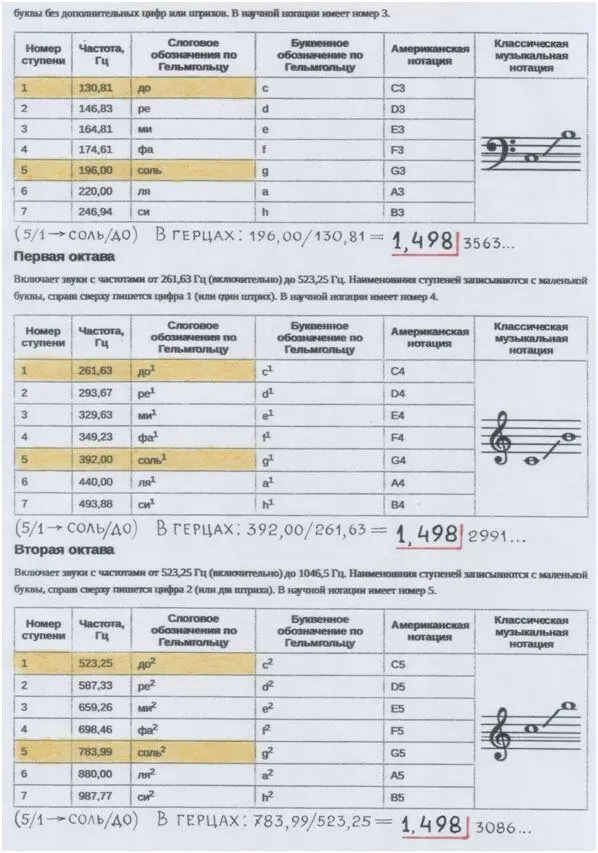
Основная таблица – из Интернет источника.Википедия.

Конечно же, Пифагор на этом не успокоился.

Он действовал как великий скульптор-ваятель – но не отдельной какой-то вещи, а всего мира – Творец! И его материалом (или материей) был не вещественный какой-то материал (камень, дерево…), а само Время, явившее себя на Земле в ЗВУКЕ.

Он взял «первоатомы» мира – квинты/доминанты – как первозданную материю/Время. Сотворил из них что-то вроде отдельного существа – сущность – ОКТАВУ. Потом нашёл главные пропорции: отношение квинты и примы, октавы и квинты. Затем, используя найденные пропорции, стал делить крупные части сотворённой октавы на всё более мелкие. Так появились новые интервалы и звуки, их выражающие: терции и их отражения-перевёртыши сексты, секунды и их отражения-перевёртыши септимы.( О кварте же мы помним, что она – отражение-перевёртыш квинты.)

Итак, сами звуки являлись слышимым выражением интервалов между собою. Но между ними возникали новые интервалы, которые выражались новыми звуками. Так появился интервал ЛИММА, И этот интервал тоже обрёл звуковое выражение. КОММА обнаружила себя сразу в звуке. Она была вначале у с л ы ш а н а. И Пифагор догадался, что она – тоже и н т е р в а л.

Микроинтервал. Так Пифагор, сотворяя космос своего музыкального строя, взошёл на новый уровень – уровень микроинтервалов и м и к р о з в у к о в.

Что он обнаружил на этом уровне?

Он опять обнаружил п о д о б и я.

Лимма вмещала четыре коммы – подобно тому как кварта вмещает четыре звука диатоники (эти звуки мы называем ступенями). Если к лимме добавить ещё одну комму, получится интервал и звук, подобный квинте в октаве.

Знакомься с ещё одним «новичком» (новичком для нас, но не для Пифагора или древних греков): АПОТОМА. Подобие квинты. Что-то вроде микроквинты.

Фрагменты статьи из Википедии

…Да, мысль Пифагора творила из звуков те же пропорции и подобия, что и Творец (Природа? Космос? Бог?). И мы сами – из тех же пропорций! Не веришь? Хочешь взглянуть на себя-человека как на Музыку?

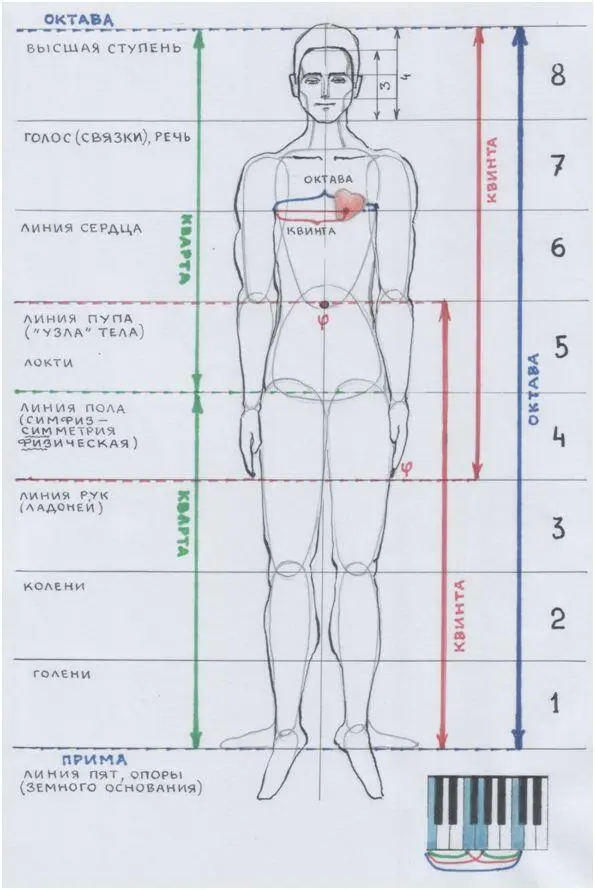
Рис. автора

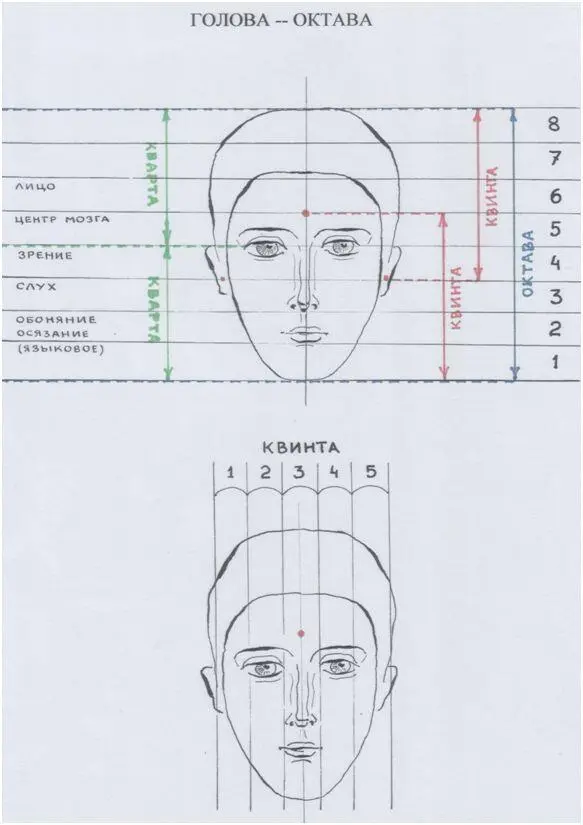
Рис. автора

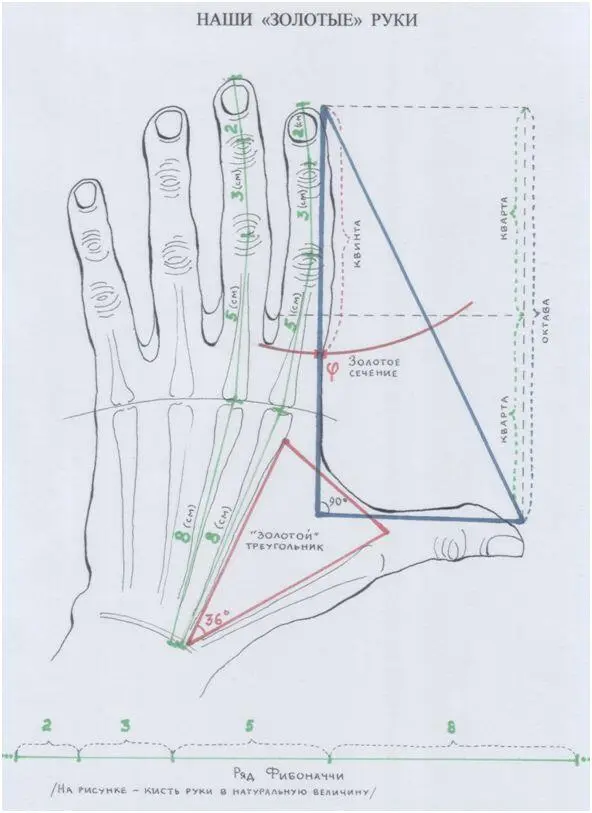
Рис. автора

Почему наше человеческое тело по своим пропорциям – ну просто идеальное подобие нашей человеческой головы? Почему?!