Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Луна плыла по волнам новолуний-полнолуний, возвращаясь к началу своего пути среди звёзд примерно каждые 355 ночей (суток).

А Земля кружилась посреди танца-кружения этих светил, между их притяжением, словно оказываясь в центре симметрии действия их могучих сил (Солнце – огромное и мощное, но очень далеко; Луна – маленькая в сравнении с Солнцем, но очень близко; силы уравновешивались).

В результате путь Земли между этими главными светилами казался замкнутым кольцом: согласие, созвучие движений всей этой космической триады (консонанс!) внутри сферы звёзд (четвёртый компонент) – всегда в одно и то же в р е м я; конец совпадал с началом, и всё повторялось из года в год.

Земля – посредине. Посредница. «Среднее арифметическое»: (365+355):2=360. 360 собственных «шагов» Земли в космических небесах, «шагов»-дуг по окружности её собственного движения-вращения.

360 г р а д у с о в.

( Градус– лат. gradus– « шаг», « ступень», « степень», « мера»).

Веками позднее египтяне эту мысль о космических ритмах жизни запечатлели в мифе о Времени.

Богиня справедливости Маат разделила год на времена:

Время разлива (Нила),

Время всходов,

Время урожая.

Все три времени года она поделила на месяцы – по четыре в каждом, и в каждом месяце – по 30 суток. А каждые сутки поделила поровну между Солнцем и Луной. Солнечный год был равен лунному: по 12 месяцев, 360 дней.

Хранительницей установленного порядка Маат назначила Луну. Но Луна не справилась со своей миссией, так как поневоле оказалась в центре ссоры между владыкой Вселенной – Великим Ра и своенравной богиней неба Нут.

Нут желала почитания, славы и могущества – не меньшего, чем у Ра.

Бог Вселенной разгневался и решил наказать тщеславную богиню неба.

«Я предаю проклятию все 360 дней года. Ни в один из этих дней ты не сможешь рожать детей и навсегда останешься бездетной!» – прогремел Ра.

Весь мир замер в страхе: что же будет?

Спасти ситуацию мог только бог мудрости (а также знаний и письменности) – Тот. Тот самый Тот, который всегда утверждал, что настоящая сила – ум.

Превратившись в ибиса, Тот полетел к хранительнице Времени Луне, удалившейся в пустыню и пребывавшей в великой печали.

Луна обрадовалась визиту дружелюбного гостя. Она желала, чтобы мгновения приятного общения с ним всё длились и длились. Не зная, чем удержать его, она вдруг предложила сыграть в шашки.

– А на что мы будем играть? – спросил Тот.

– У меня ничего нет, кроме света, которым я освещаю небо по ночам, – смутилась Луна.

– Будем играть на свет, – согласился Тот. – Не на весь, конечно. На часть.

В лунном году 360 дней. Возьми от каждого дня маленькую-маленькую часть, затем сложи эти части вместе – они и будут ставкой.

– Это невозможно, – огорчилась Луна. – Я хранительница Времени, я не могу отдать ни одного дня из лунного года.

– Не надо целого дня, – улыбнулся Тот. – Убавь от каждого дня всего по нескольку минут. 24/72 = 1/3 часа = 20 минут…

– Я убавлю от каждого дня маленький кусочек – всего 1/72 его часть, если ты, Тот, выиграешь. Даже никто не заметит, что лунные сутки стали короче, – согласилась Луна.

Тот кивнул, и игра началась.

…Тот выиграл.

Убавив от каждого дня всего несколько минут, Луна, как оказалось, получила значительный проигрыш. Когда Тот сложил эти минуты, вышло целых 5 суток! Отныне в лунном году осталось 355 дней.

А выигранные 5 дней Тот прибавил к солнечному году, в результате чего в солнечном году стало 365 дней.

В чём была хитрость Тота? – Выигранные им у Луны 5 дней не были преданы проклятию Ра! Ведь Ра проклял 360 дней, а не 365.

И выигранные дни Тот посвятил самому Ра. – Не станет же Владыка проклинать дни, посвящённые ему самому.

А Нут в эти 5 дней в конце года родила пятерых детей: Осириса, Гора Бехдетского, Сета, Исиду и Нефтиду, – тоже богов.

(И.В. Рак. Мифы и сказки древнего Египта.)

/Пересказ автора/

Эту самую 1/72 часть можно получить, если разделить окружность в 360˚ на 5 частей: по 72˚ каждая часть. И 1/72 часть каждой пятой части окружности будет равна 1˚. В пересчёте на дни 1˚ = 1 день. 5˚= 5дням.

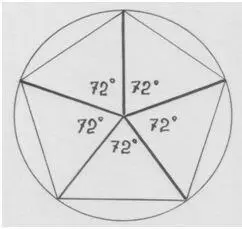
Рис. автора.

Лунный год будет выглядеть разомкнутым кольцом, а солнечный год – намёком на спираль. При этом получается, будто в каждой пятой части пятиугольника должен бы «набегать» один лишний градус – 73-й. А «по-лунному» – в каждой части 71 градус.

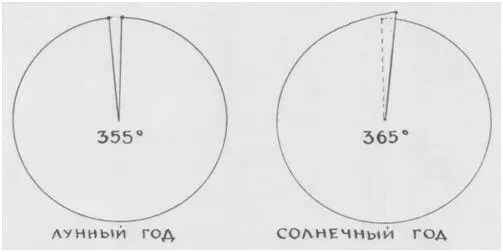
Рис. автора.

Замечательно то, что в ЦЕЛОМ и в каждой пятой части этого ЦЕЛОГО отношения остаются одинаковыми:

365/360 = 1, 0138888… 73/72 = 1, 0138888…

360/355 = 1, 0140845… 72/71 = 1, 0140845…

То есть, в данном случае в ЧАСТИ отражается ЦЕЛОЕ настолько полно, что даже можно поставить знак равенства.

Какие чудесные перспективы сулило это обстоятельство для Мысли Пифагора!

Звуковые консонансы – той же природы, что и космические! Вот она, пифагорова «музыка сфер»! Сферы небесных тел (Солнца, Земли, Луны, «неподвижных звёзд») в своём гармоничном согласии/созвучии подобны музыке! А музыка – рождена космосом, Вселенной! Всё – единый узел.

«10» – священное число! (Земля между Солнцем и Луной внутри звёздной сферы.)

И в самом деле, это ведь число двойного узла: правого и левого. Их совмещение рождает Пентаграмму – само совершенство Золотого сечения (хотя Пифагор не употреблял этого термина, как ты знаешь; но он постиг саму с у т ь этого явления, пронизывающего великое во Вселенной и малое на Земле). Это – взаимодействие квинт, прародительниц музыкального строя (квинт и их перевёртышей-кварт).

Да, всего лишь разница-разность между солнечным и лунным годом на Земле (10 дней – 10 градусов) и – поразительное совпадение звуковых консонансов в «пункте 72» плюс-минус крошка-комма.

«10» для Пифагора – число, к тому же, особое ещё и потому, что т р е у г о л ь н о е. Странно?

Если в д у м а т ь с я – то не странно.

Равносторонний треугольник знаменует собою идею совершенства-равенства: равенства сторон-отрезков и углов. Он подобен явлению «градуса» – меры, которой измеряют и углы, и дуги (углы и отрезки окружности).

В равносторонний треугольник вписывается само число «10» в виде точек-«узелков», скрепляющих внутренние подобные малые треугольники:

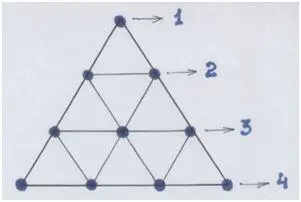
Рис. автора.

А теперь давай ещё разочек взглянём на уже известную нам таблицу гармоник, на ту её часть, где представлены совершенные консонансы в виде волн, бегущих туда-обратно: