Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

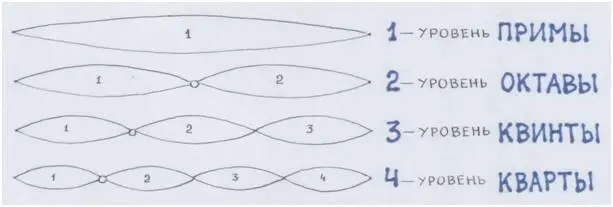
Рис. автора.

Совместим геометрический и волновой образы:

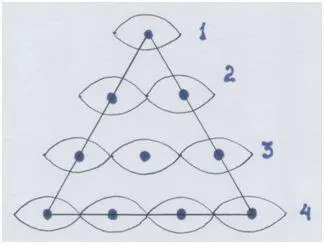
Рис. автора.

Попробуем совместить так, чтобы узлы совпадали. (У бегущих туда-обратно звуковых волн есть у з л ы и так называемые п у ч н о с т и. Об этом ты можешь узнать из книги проф. А.Г.Белявского «Теория звука в приложении к музыке»). Так нам треугольник покажет именно частоты или длины волн интервалов-консонансов в виде отношений/пропорций/дробей.

Рис. автора.

Музыкальный (и космический, конечно же) треугольник!

Музыкальная «десятка»!

Особенность всех чисел, принимающих участие в этой «магии» такова, что при сложении они и образуют «десятку»: 1+2+3+4 = 10

О, как непросто всё было у Пифагора!

Всё связано со всем.

А как же Пифагор поступил с КОММОЙ?

Комма своим явлением словно намекала на солнечное время на Земле (спираль солнечного года). Согласно Боэцию, она п р е в ы ш а л а консонанс диапазона-октавы («перехлёстывала через край»). Как солнечное время на Земле «перехлёстывает» кольцо в 360˚ на 5˚ (дней). На 1/72.

(Вот ещё раз: Звук и Время на Земле – одной природы, – космической!)

Те, кто думают, что Пифагор остановился, преткнулся о тот факт, что реальный звук словно не желает строго подчиняться консонансу (торопится вслед за Солнцем), они говорят, что пифагоров строй подобен спирали.

Но давай вглядимся повнимательнее в измерительный прибор Пифагора – монохорд: ящик. На ящике – шкала с делениями. Струна. Один конец струны закреплён жёстко колком, похожим на гвоздь. А другой конец струны свисает свободно. Он перекинут через колёсико-блок, и к нему подвешен груз. Ещё есть передвижная перекладина ( её называют «кобылкой», – наверное, потому что бегает туда-сюда) для изменения пропорций струны – чтобы получать различные интервалы-звуки.

Но нас интересует свободный конец струны. Для чего так?

Воспитывать КОММУ! Сдерживать её слишком солнечный темперамент. Приучать её к к о н с о н а н с у.

Пифагор был тем ещё Тотом! Только поступил он противоположно, и благодаря этому Луна получила возможность отыграться – вернуть свою 1/72 долю. Как?

Если частота звука слегка зашкаливает, то есть чуть выше, чем необходимо для консонанса, эту частоту можно изменить: понизить, уменьшить, – изменив натяжение струны, чуть ослабив его. Струна станет толще, «массивнее», «ленивее», будет колебаться менее активно. И напряжение звуковой волны уменьшится, и звук понизится в тоне. И комма вернётся в рамки диапазона. Кольцо замкнётся.

Для этого придётся вернуть 1/72 долю шкалы консонансов ( на нашей ленте частот) Луне. 73/72-х станут 72/72.

Как мог действовать Пифагор?

Сама проблема с коммой, по-видимому, возникла, когда пришлось приводить к консонансу звучание нескольких струн, изначально настроенных в соответствии с расчётами интервалов. Для этой цели служил другой прибор: полихорд (греч. polys – «многий», множество, horda – струна).

На этом приборе мы видим четыре струны для основных консонансов: примы, октавы, квинты, кварты.

Примой может стать любой тон-звук. От него и будут выстраиваться все остальные соотношения звуков. Разница в комму проявит себя на октавной струне (73/72= 1,0138888…). Она натянута в два раза сильнее струны примы (если жильная струна), или в два раза тоньше (если металлическая). Её натяжение нужно уменьшить на 1/72 (0,0138888….) и ещё совсем чуть-чуть. Об этом «чуть-чуть», может быть, ещё поговорим, если не устанем.

То есть:

Идеальная шкала консонансов по расчёту должна быть 72/72. Но при этом мы слышим звук на 1/72 выше расчетного, – как если бы шкала была 73/72. Чтобы услышать консонанс 72/72, нам нужно спуститься до отметки 71 (ослабить натяжение струны) – «по Луне». Тогда мы опять услышим звук на 1/72 выше, над отметкой 71,– т.е. 72/72.

Струна квинты (если жильная) натянута в полтора раза сильнее струны примы ( как если бы мы растянули 72 деления на длину 108; 72х1,5=108), или толщина её (если струна металлическая) = 2/3 толщины струны примы.

Что мы услышим? – Мы услышим звук тоже примерно на 1/72 выше нужного, т.е. не 108/72, а 109/72. Нам нужно ослабить натяжение струны до отметки 107 («по Луне»), и ещё чуть-чуть. Мы услышим то, что нужно: 0,0138888…х 108= 1,499…– «чуть-чуть».

Аналогично – со струной кварты.

Струна кварты (если жильная) натянута в 4/3 раза (примерно в 1,33333…. раза) сильнее струны примы (как если бы мы растянули 72 деления на на почти 96: 1,333333…х 72 = 95,999999…), или толщина струны (если струна металлическая) = ¾ струны примы.

Что мы услышим? – Мы услышим звук также примерно на 1/72 выше нужного, т.е. не 96/72, а 97/72. Нам нужно ослабить натяжение струны «по Луне», чтобы мы услышали необходимую высоту звука: 95/72 – «чуть-чуть».

Так можно поступать со струнами и для других интервальных звуков. На полихорде можно разместить и 6, и 7 струн для этих целей, – смоделировав таким образом лиру.

Странно ведёт себя звук. Мы слышим его «по Солнцу», а струны, чтобы получить консонансы, нужно настраивать «по Луне».

И здесь тоже не всё так просто, как в египетском мифе о Времени. Ведь солнечный год чуть больше 365 дней, за 4 года набегает своя «комма» примерно в одни сутки. Да и лунный год – не ровно 355 дней. Мы округляем, чтобы увидеть главные пропорции, увидеть структуру. Мы привыкли всё сводить к завершённости, к уравнениям. А движение существует благодаря неравенствам – пусть небольшим, с разницей в «чуть-чуть», но неравенствам.

Звук, как и Время, происходит из движения. Сами волны – это движение. Движение подразумевает какое-то неравенство. И конечно же, консонансы не могут быть идеальными. И наш слух готов мириться с небольшими неравенствами, которые держатся на «чуть-чуть». Мы их как будто не слышим – «округляем», как иррациональные числа мы склонны округлять.

Кстати, если ты когда-нибудь всё-таки заглянёшь в книгу А.Г.Белявского «Теория звука в приложении к музыке», ты узнаешь из рекомендаций настройщикам фортепиано, что чистые интервалы при настройке необходимо понижать – иначе консонансов не получится, настройка инструмента потерпит крах.

Пифагор об этом узнал из правил поведения космических объектов и обнаружил эти же правила в поведении звуков.

И Генрих Рудольф Герц, физик 19 века, «изобретатель» герца– единицы измерения частоты периодических процессов, в том числе волн, похоже, не противоречил Пифагору, соединившему космос, время, звук. Герцслужит также единицей измерения времени.