Александр Козлов - Математика флота. Фантастика и реальность

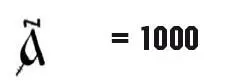
Десятки тысяч назывались «тьма», их обозначали, обводя знаки единиц кружками:

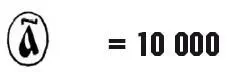
Отсюда произошло выражение «Тьма народу»,т. е. очень много народу.

Сотни тысяч назывались «легионами»,их обозначали, обводя знаки единиц кружками из точек:

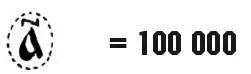
Миллионы назывались «леодрами».Их обозначали, обводя знаки единиц кружками из лучей или запятых:

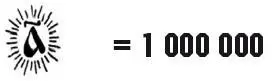
Десятки миллионов назывались «воронами» или «вранами»и их обозначали, обводя знаки единиц кружками из крестиков или ставя по обе стороны букву К:

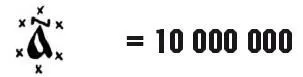
Сотни миллионов назывались «колодами».«Колода» имела специальное обозначение – над буквой и под буквой ставились квадратные скобки:

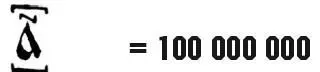
Иероглифы жителей Древнего Вавилонасоставлялись из узких вертикальных и горизонтальных клинышков, эти два значка использовались и для записи чисел. Один вертикальный клинышек обозначал единицу, горизонтальный – десяток. В Древнем Вавилоне считали группами по 60 единиц. Например, число 185 представлялось как 3 раза по 60 и еще 5. Записывалось такое число с помощью всего двух знаков, один из которых обозначал, сколько раз взято по 60, а другой – сколько взято единиц.

О том, когда и как возникла у вавилонян шестидесятеричнаясистема, существует много гипотез, но ни одна пока не доказана. Одна из гипотез, состоит в том, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое – десятичной. Шестидесятеричная система возникла как компромисс между этими двумя системами. Другая гипотеза состоит в том, что вавилоняне считали продолжительность года равной 360 суткам, что, естественно, связывают с числом 60.

Шестидесятеричная системав некоторой степени, сохранилась до наших дней, например, в делении часа на 60 минут, а минуты – на 60 секунд и в аналогичной системе измерение углов: 1 градус равен 60 минутам, 1 минута-60 секундам.

Двоичной системой счисленияпользовались при счете некоторые первобытные племена, она была известна еще древнекитайским математикам, но по-настоящему развил и построил двоичную систему великий немецкий математик Лейбниц, видевший в ней олицетворение глубокой метафизической истины.

Двоичной системой счисления пользуютсянекоторые (местные) культуры в Африке, Австралии и Южной Америке.

Для изображения чисел в двоичной системе счисления требуется лишь две цифры: 0 и 1. По этой причине двоичную запись числа легко представить, пользуясь физическими элементами, которые имеют два различных устойчивых состояния. Именно это и послужило одной из важных причин широкого использования двоичной системы в современных электронных вычислительных машинах.

Самой экономичной из всех систем счисленияявляется троичная.Двоичная и равносильная ей, в смысле экономичности, четверичная системы, несколько уступают в этом отношении троичной, но превосходят все основные возможные системы. Если для записи чисел от 1 до 10 в десятичной системе требуется 90 различных состояний, а в двоичной -60, то в троичной системе достаточно 57 состояний.

Наиболее привычная ситуация, в которой проявляется необходимость троичного анализа, – это, пожалуй, взвешивание на чашечных весах. Здесь могут возникнуть три разных случая: либо одна из чашек перевесит другую, либо наоборот, либо же чашки уравновесят друг друга.

Четверичной системой счисления пользуются,главным образом, индейские племена Южной Америки и индейцы юкки в Калифорнии,считающих на промежутках между пальцами.

Пятеричная системасчисления была распространена гораздо шире, чем все остальные. Индейцы племени тама-накос в Южной Америке употребляют для обозначения числа 5 то же слово, что и для обозначения «всей руки». Слово «шесть» по-таманакски означает «один палец на другой руке», семь – «два пальца на другой руке» и т. д. для восьми и девяти. Десять называется «двумя руками». Желая назвать число от 11 до 14, таманакос протягивают вперед обе руки и считают: «один на ноге, два на ноге» и т. д. до тех пор, пока не доходят до 15 – «всей ноги». Затем следует «один на другой ноге» (число 16) и т. д. до 19. Число 20 по-таманакски означает «один индеец», 21 – «один на руке другого индейца». «Два индейца» означают 40, «три индейца» – 60. У жителей древней Явы и у ацтеков продолжительность недели составляла 5 дней. Некоторые историки считают, что римское число X (десять) составлено из двух римских пятерок V (одна из них перевернута), а число V в свою очередь возникло из стилизованного изображения человеческой руки.

Широкое распространение имела в древности двенад-цатеричная система счисления.Происхождение ее тоже связано со счетом на пальцах. А именно, так как четыре пальца руки (кроме большого) имеют в совокупности 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимают за единицу следующего разряда. Основное преимущество двенадцатеричной системы состоит в том, что ее основание делится без остатка на 2, 3 и 4. Сторонники двенадцатеричной системы появились еще в XVI веке. В более позднее время к их числу принадлежали столь выдающиеся люди, как Герберт Спенсер, Джон Квинси Адамс и Джордж Бернард Шоу. Существует даже американское двенадцатеричное общество, выпускающее два периодических издания: «Двенадцатеричный бюллетень» и «Руководство по двенадцатеричной системе». Всей «двенадцатеричников» общество снабжает специальной счетной линейкой, в которой в качестве основания используется 12.

В устной речи остатки двенадцатеричной системы сохранились и до наших дней:вместо того, чтобы сказать «двенадцать», часть говорят «дюжина».Сохранился обычай считать многие предметы не десятками, а именно дюжинами, например, столовые приборы в сервизе (сервиз на 12 персон) или стулья в мебельном гарнитуре.