Марина Васильева - Инженерная графика

Ту же задачу можно выполнить с помощью линейки и угольника с углами 30 и 60° (рисунок 4). Гипотенуза угольника при этом должна проходить через центр окружности.

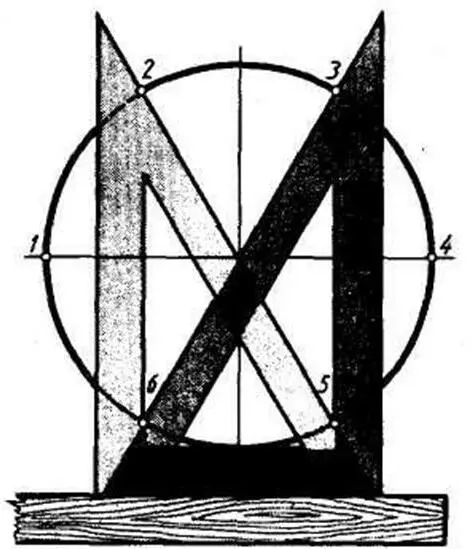
Рисунок 4 – Деление окружности на шесть равных частей с помощью угольника

Деление окружности на восемь равных частей . Точки 1, 3, 5, 7 лежат на пересечении центровых линий с окружностью (рисунок 5). Еще четыре точки находят с помощью угольника с углами 45°. При получении точек 2, 4, 6, 8 гипотенуза угольника проходит через центр окружности.

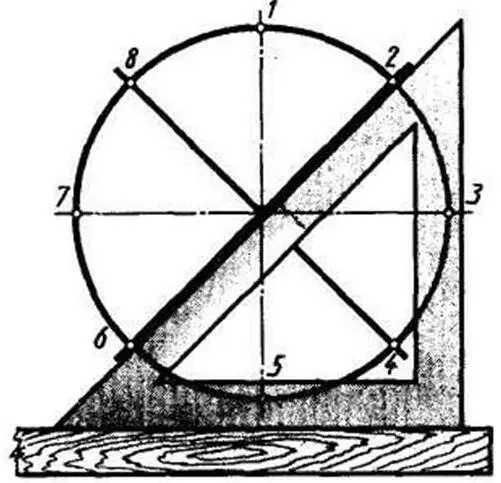
Рисунок 5 – Деление окружности на восемь равных частей с помощью угольника

Деление окружности на любое число равных частей . Для деления окружности на любое число равных частей пользуются коэффициентами, приведенными в таблице 1.

Длину l хорды, которую откладывают на заданной окружности, определяют по формуле:

где l – длина хорды;

d – диаметр заданной окружности;

k – коэффициент, определяемый по таблице 1.

Чтобы разделить окружность заданного диаметра 90 мм, например, на 14 частей, поступают следующим образом.

Таблица 1 – Коэффициенты для деления окружности

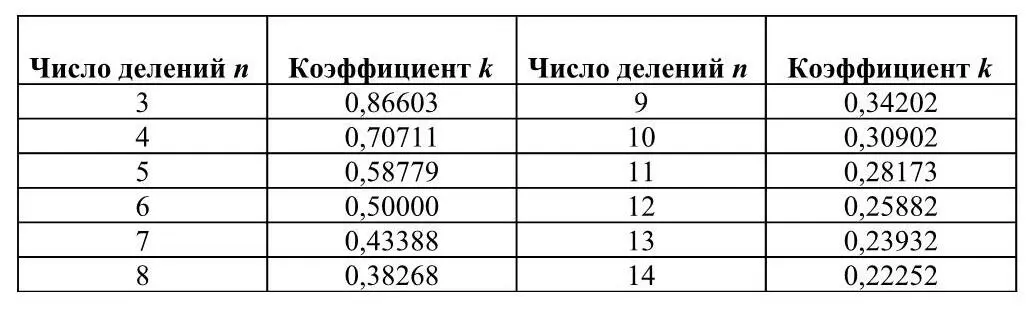
В первой графе таблицы 1 находят число делений n , т.е. 14. Из второй графы выписывают коэффициент k , соответствующий числу делений n . В данном случае он равен 0,22252. Диаметр заданной окружности умножают на коэффициент и получают длину хорды:

Полученную длину хорды откладывают циркулем-измерителем 14 раз на заданной окружности.

Нахождение центра дуги и определение величины радиуса . Задана дуга окружности, центр и радиус которой неизвестны.

Для их определения нужно провести две непараллельные хорды (рисунок 6,а) и восставить перпендикуляры к серединам хорд (рисунок 6,б). Центр О дуги находится на пересечении этих перпендикуляров.

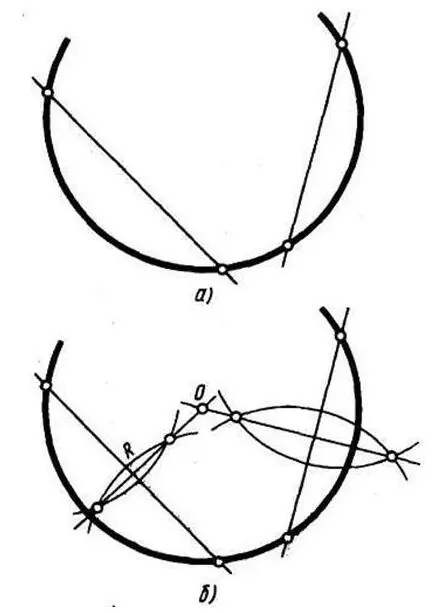
Рисунок 6 – Определение центра дуги

1. Что называют анализом графического состава изображений?

2. Для чего нужен анализ графического состава изображения?

3. Какими линиями выполняют вспомогательные построения?

Упражнение 1. С помощью линейки и угольника постройте углы 30, 60, 120, 75, 15 и 105°.

Упражнение 2. Разделите отрезок прямой на четыре равные части; на восемь равных частей; на 12 равных частей.

Упражнение 3. Разделите тупой угол на четыре равные части.

Упражнение 4. Разделите прямой угол на три равные части с помощью циркуля и линейки. Постройте угол 30°. Разделите окружность на три равные части.

Упражнение 5. С помощью угольника и линейки разделите окружность на шесть равных частей (на 12). То же самое сделайте с помощью циркуля.

Упражнение 6. Разделите окружность на восемь равных частей наиболее рациональным способом.

Упражнение 7. Подсчитайте, чему равна длина хорды при делении окружности диаметра 100 мм на пять равных частей; окружности диаметра 120 мм на 14 равных частей; окружности диаметра 200 мм на 11 равных частей.

Упражнение 8. Вычертите чертеж угольника (рисунок 7).

Упражнение 9. Выполните один из чертежей прокладок, приведенных на рисунке 8 а, б, в, г, д, е.

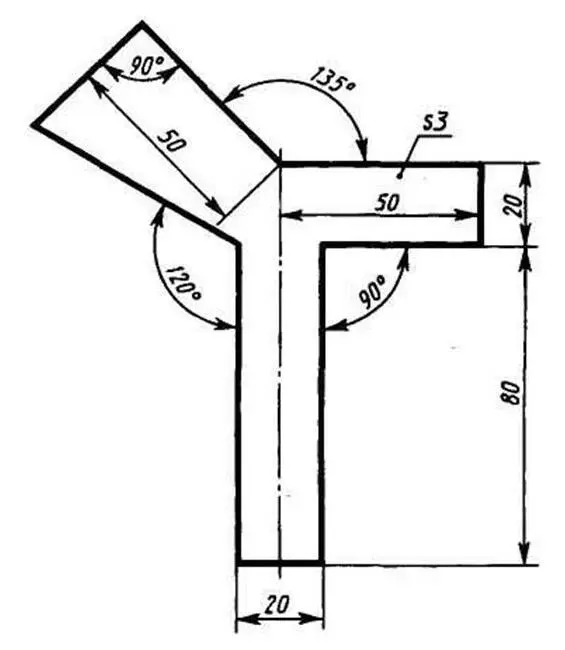
Рисунок 7 – Задание для упражнений

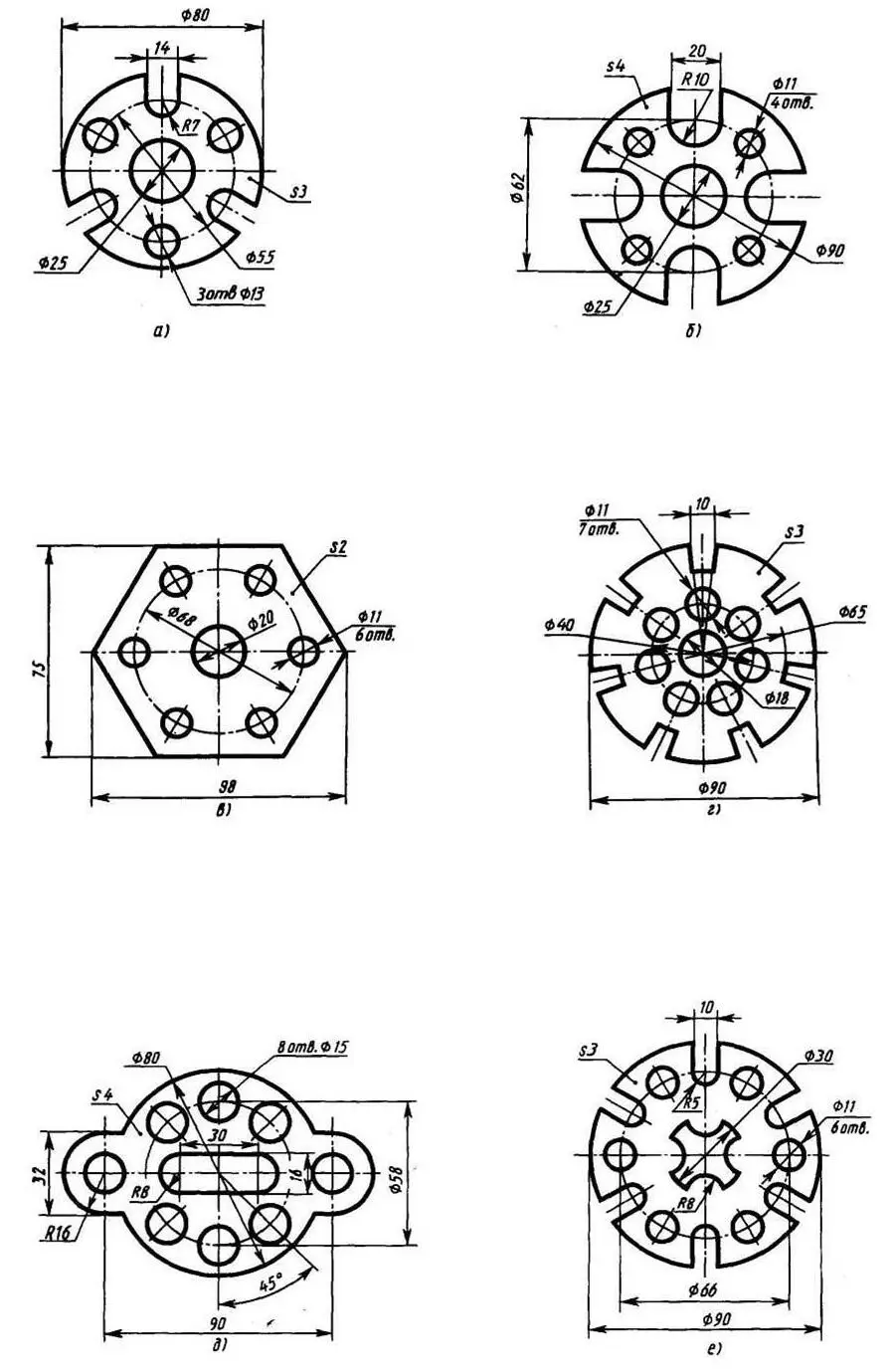
Рисунок 8 – Задания для упражнений

При выполнении машиностроительных чертежей, а также при разметке заготовок деталей на производстве часто приходится плавно соединять прямые линии с дугами окружностей или дугу окружности с дугами других окружностей, т. е. выполнять сопряжение.

Сопряжением называют плавный переход отрезка прямой в дугу окружности или дуги одного радиуса в дугу другого радиуса.

Для построения сопряжений необходимо знать величину радиуса сопряжения, определить центры, из которых проводят дуги, т.е. центры сопряжений (рисунок 9). Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений. При построении чертежа сопрягающиеся линии нужно доводить точно до этих точек.

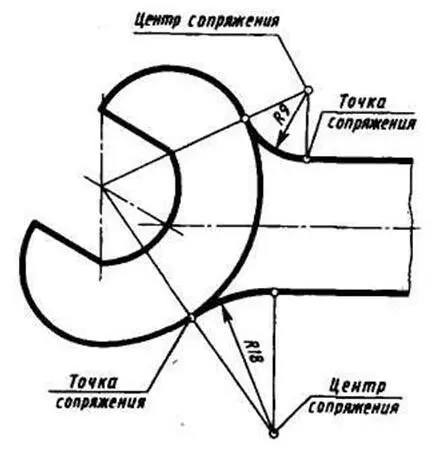
Рисунок 9 – Элементы сопряжений

Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую (рисунок 10,а), или на линии, соединяющей центры сопрягаемых дуг (рисунок 10б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку (точки) сопряжения.

Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рисунок 11а). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

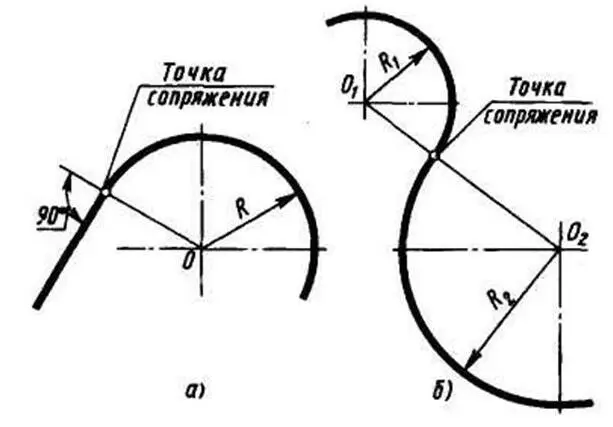
Рисунок 10 – Определение точки сопряжения

Для всех трех случаев можно применять следующее построение.

Находят точку О – центр сопряжения, который должен лежать на расстоянии R от сторон угла, т. е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них (рисунок 11б).

1. Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные (рисунок 11б).

2. Находят точки сопряжений (рисунок 11в). Для этого из точки 0 опускают перпендикуляры на заданные прямые.

3. Из точки 0, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рисунок 11в).

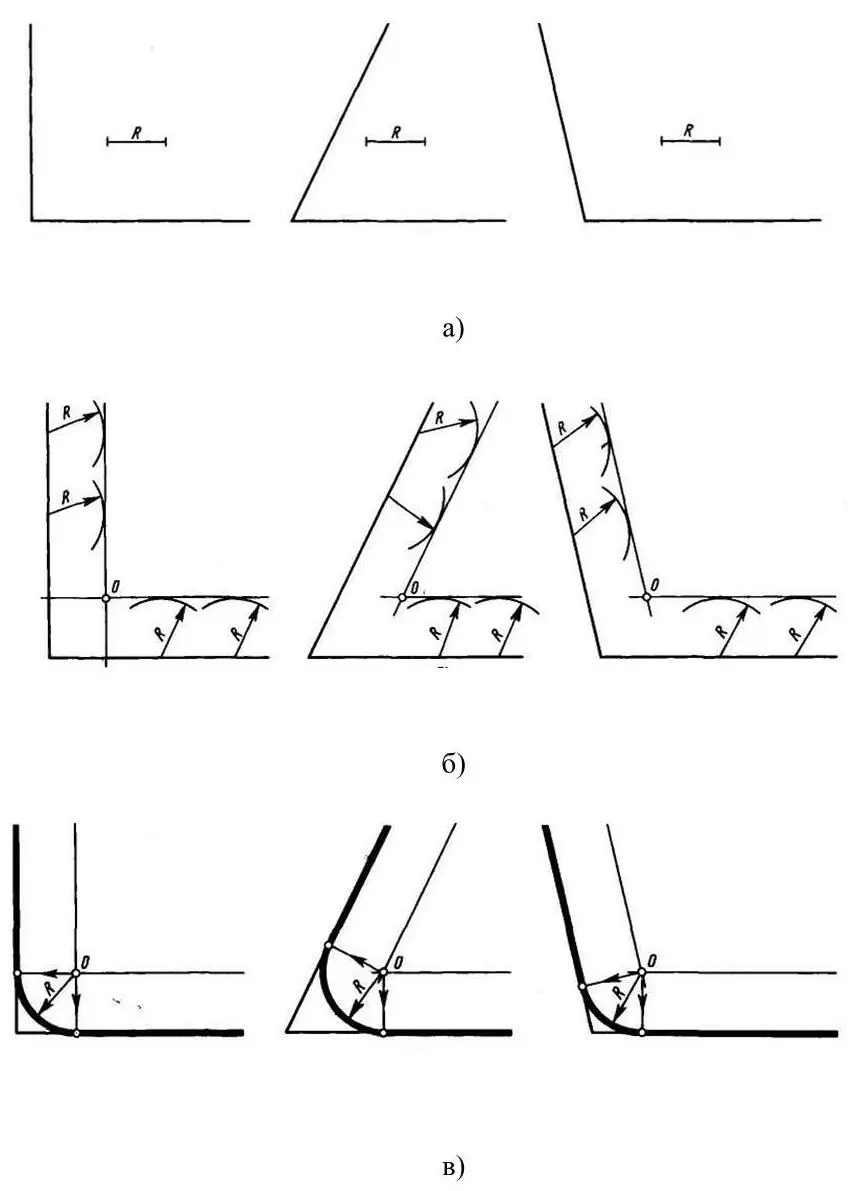
Рисунок 11 – Построение сопряжения двух пересекающихся прямых

Сопряжение трёх пересекающихся прямых. Положение центра сопрягаемой окружности определяется точкой пересечения биссектрис углов. Радиус окружности (дуги сопряжения) равен длине перпендикуляра, опущенного из центра 0 на любую из заданных прямых (рисунок 12).