Марина Васильева - Инженерная графика

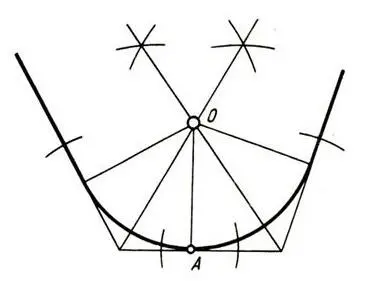
Рисунок 12 – Сопряжение трёх пресекающихся прямых

Сопряжение двух параллельных прямых. Заданы две параллельные прямые и на одной из них точка сопряжения М (рисунок 13а). Требуется построить сопряжение.

Построение выполняют следующим образом:

1) находят центр сопряжения и радиус дуги (рисунок 13б). Для этого из точки М восставляют перпендикуляр до пересечения с прямой в точке N.

Отрезок прямой MN делят пополам;

2) из точки О – центра сопряжения радиусом OM = ON описывают дугу от точек сопряжения М и N (рисунок 13 в).

Упражнение. Выполните чертеж шаблона (рисунок 14), применив правила построения сопряжений. Линии построений не стирайте. Нанесите размеры и обозначения шероховатости поверхностей, имея в виду, что внутренние поверхности шаблона должны иметь шероховатости Ra 0,80, а остальные Rг 12,5. Масштаб 1:1. Заполните основную надпись (материал – сталь 45 по ГОСТ 1050-88).

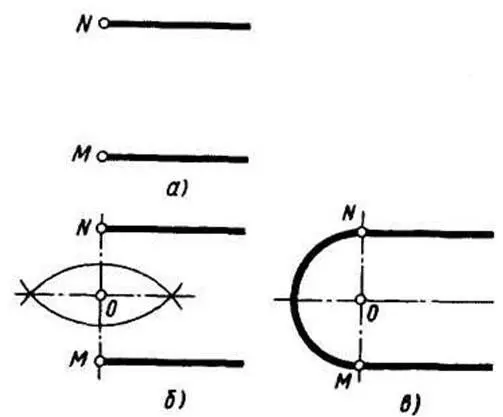
Рисунок 13 – Построение сопряжения двух параллельных прямых

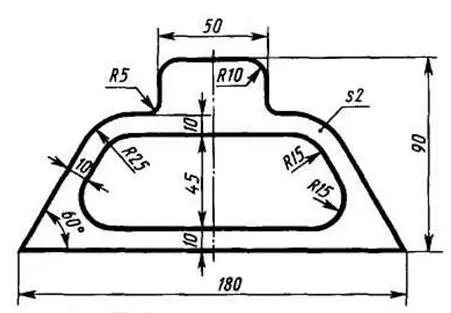
Рисунок 14 – Задание для упражнений

Сопряжение дуги окружности и прямой линии дугой заданного радиуса.

Внешнее касание (рисунок 15а). Центр 01 дуги сопряжения находится на пересечении вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R1, и дуги радиуса R + R1 из центра 0. Точки сопряжения K и M находятся соответственно в основании перпендикуляра 01K и на пересечении прямой 001 с основной окружностью.

Внутреннее касание (рисунок 15б). Центр 01 дуги сопряжения находится на пересечении вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R, и дуги радиуса R − R1 из центра 0. Точки сопряжения – соответственно в основании перпендикуляра 01 K и на пересечении продолжения луча 001 с основной окружностью.

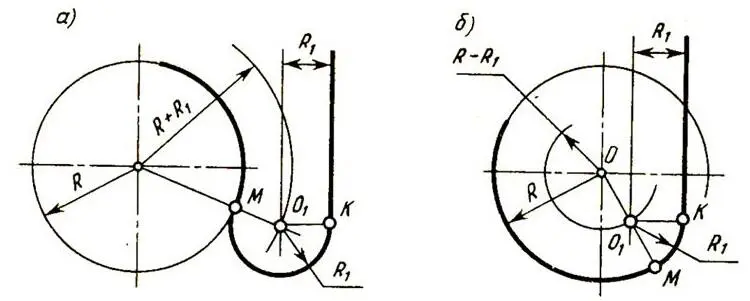
Рисунок 15 – Сопряжение дуги окружности и прямой линии дугой заданного радиуса: а – внешнее касание, б – внутреннее касание.

Сопряжение окружности и прямой при условии, что дуга сопряжения проходит через заданную точку А на окружности (рисунок 16).

Центр дуги сопряжения определяется точкой пересечения луча OA, проведённого через точку сопряжения А и центр O заданной окружности, и биссектрисы угла ABK, образованного касательной AB в точке сопряжения и заданной прямой t. Радиус сопрягающей дуги равен расстоянию O 1A; O 1K⊥ t, где K – точка сопряжения на прямой t.

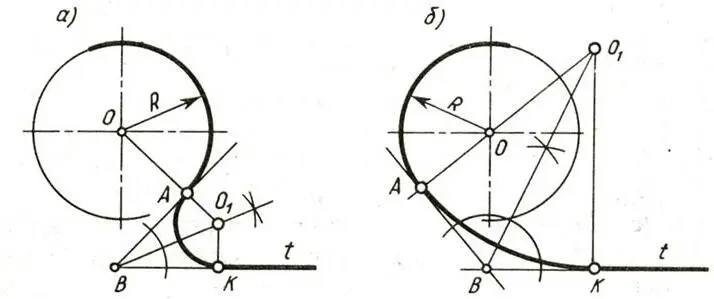
Рисунок 16 – Сопряжение окружности и прямой при заданной точке сопряжения на окружности: а – внешнее касание, б – внутреннее касание.

Построение окружности, проходящей через данную точку A и касаю щейся данной окружности м центром O в заданной точке B (рисунок 17, 18, 19). Центр O 1дуги сопряжения определяется точкой пересечения луча, проведённого через центр O заданную точку сопряжения B, с перпендикуляром, восстановленным из середины хорды AB; O 1B – радиус искомой окружности.

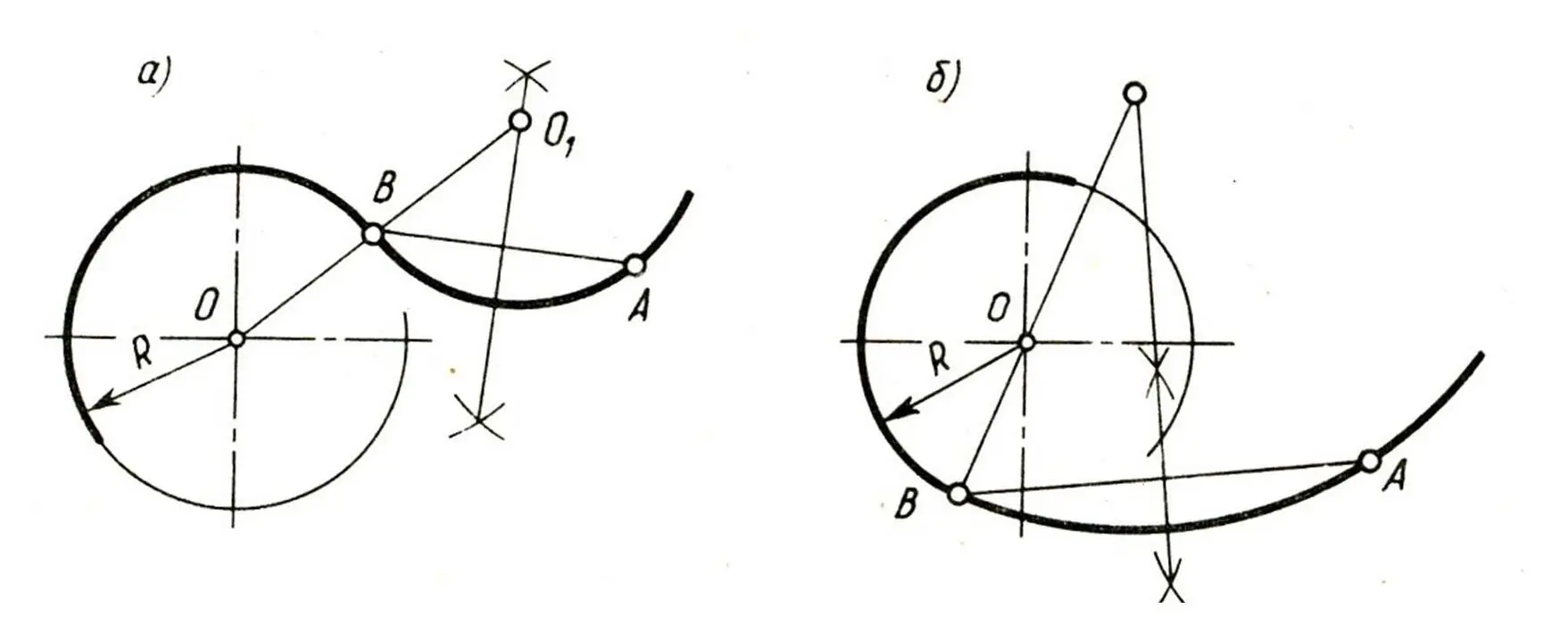
Рисунок 17 – Сопряжение окружности в заданной точке B с окружностью, проходящей через заданную точку A: а – внешнее касание, б – внутреннее касание.

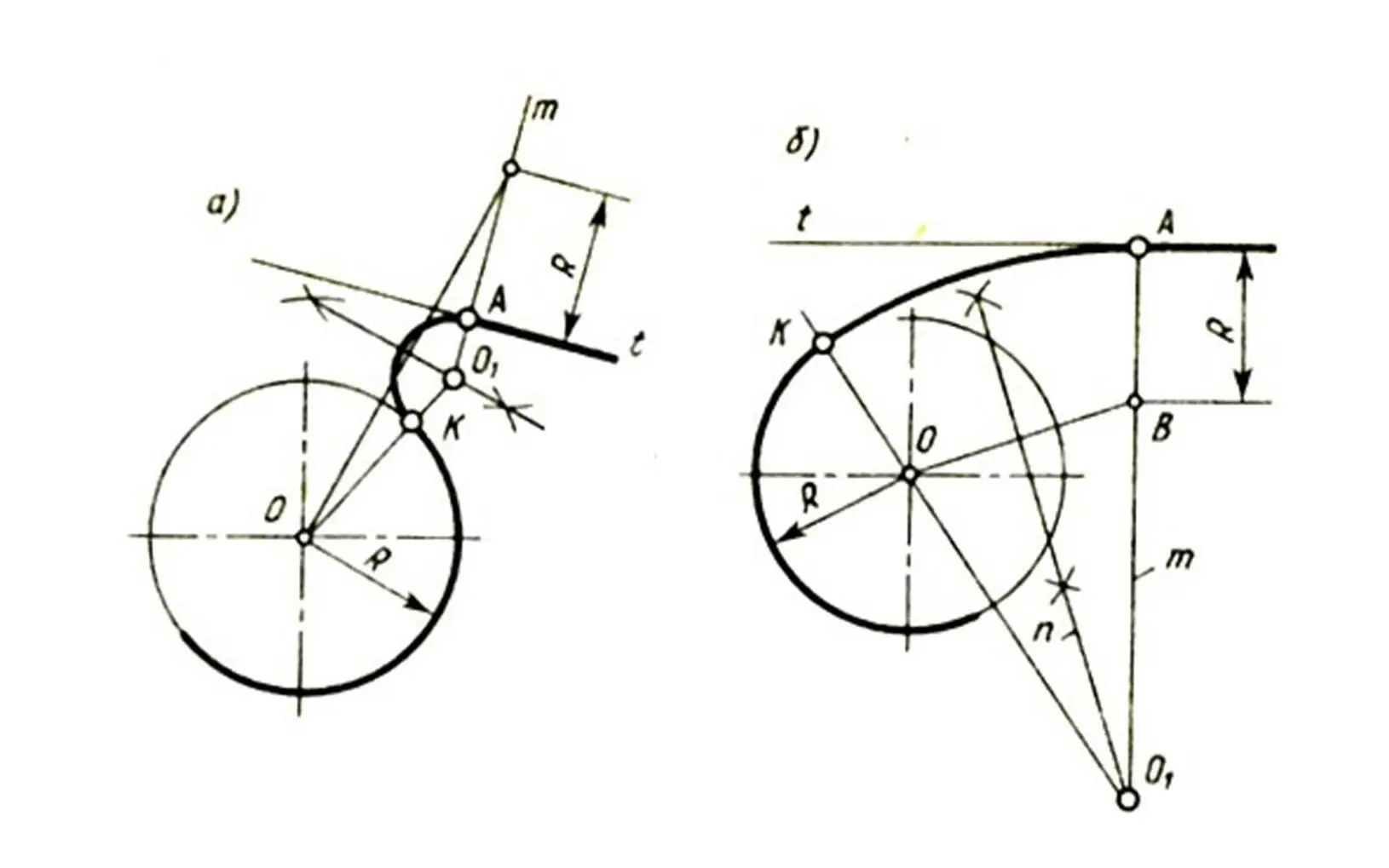
Рисунок 18 – Проведение касательной к окружности

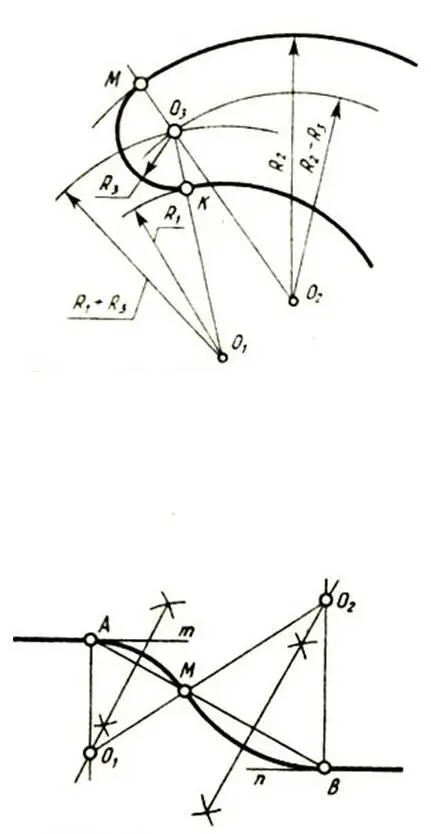
Рисунок 19 – Сопряжение дуг окружностей

Проведение касательной к окружности. Даны окружность с центром О и точка А. Провести из точки А касательную к окружности.

1. Точку А соединяют прямой с заданным центром О окружности. Строят вспомогательную окружность диаметром, равным ОА (рисунок 20а). Для определения центра О1, делят отрезок ОА пополам.

2. Точки М и N являются точками пересечения вспомогательной окружности с заданной – искомые точки касания. Точку А соединяют прямыми с точками М или N (рисунок 20б). Прямая AM будет перпендикулярна прямой ОМ, так как угол АМО опирается на диаметр.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.