Коллектив авторов - Краткий курс по статистике
- Название:Краткий курс по статистике
- Автор:
- Жанр:
- Издательство:Литагент РИПОЛ
- Год:2015
- Город:Москва
- ISBN:978-5-409-00639-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Коллектив авторов - Краткий курс по статистике краткое содержание
Издание предназначено для студентов высших учебных заведений.
Краткий курс по статистике - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
5. Различают следующие относительные показатели вариации: коэффициент осцилляции, коэффициенты вариации.
Коэффициент осцилляции ( V R):
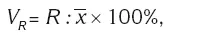
где R – размах вариации;
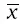 – средняя. Обычно имеет значение больше единицы, поскольку размах вариации в основном бывает больше средней величины.
– средняя. Обычно имеет значение больше единицы, поскольку размах вариации в основном бывает больше средней величины.
Линейный коэффициент вариации ( 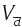 ) показывает, какую часть в размере средней величины (или в объеме медианы) составляет размер среднего линейного отклонения:
) показывает, какую часть в размере средней величины (или в объеме медианы) составляет размер среднего линейного отклонения:
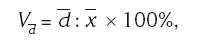
или
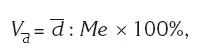
где 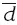 – среднее линейное отклонение;
– среднее линейное отклонение;
Ме – медиана.
Коэффициент вариации (V σ) определяет удельный вес среднего квадратического отклонения в размере средней величины и служит мерой однородности совокупности:
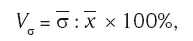
где σ – среднее квадратическое отклонение. Совокупность считается однородной, если значение данного показателя не превышает 33 %.
Эмпирический коэффициент детерминации (η 2) отражает определенную изменением признака-фактора долю вариации результативного признака:
η 2 = δ 2: δ 2 общ,
где δ 2– межгрупповая дисперсия;
δ 2 общ– общая дисперсия.
Эмпирическое корреляционное отношение (η) определяет тесноту связи между изменением признака-фактора и последующим изменением признака-результата – корень из коэффициента детерминации:
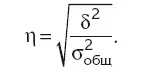
Чем ближе к единице значение эмпирического корреляционного отношения, тем теснее связь между изменением признака-фактора и признака-результата.
10. Дисперсия
1. Различают невзвешенную и взвешенную дисперсии.
Дисперсия (σ 2) – сумма квадратов отклонений значений показателя от средней.
Дисперсия невзвешенная
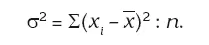
Дисперсия взвешенная
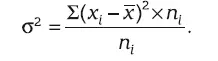
Если необходимо не только изучить вариации признака совокупности, но и исследовать количественные изменения признака по однородным группам совокупности, то помимо общей средней для всей совокупности необходимо просчитывать и частные средние величины по отдельным группам.
Выделяют общую и среднюю виды дисперсий.
Общая дисперсия характеризует изменчивость признака всей совокупности под влиянием всех определивших данную вариацию факторов:
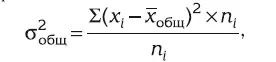
где 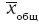 – общая средняя арифметическая всей исследуемой совокупности.
– общая средняя арифметическая всей исследуемой совокупности.
Средняя внутригрупповая дисперсия 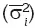 показывает случайную вариацию, возникающую под влиянием неучтенных факторов. Она не зависит от положенного в основу группировки признака-фактора.
показывает случайную вариацию, возникающую под влиянием неучтенных факторов. Она не зависит от положенного в основу группировки признака-фактора.
2. Разработаны следующие основные этапы расчета дисперсии:
✓ рассчитывается дисперсия (σ i 2) по отдельным группам:
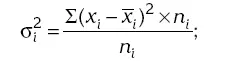
✓ рассчитывается средняя внутригрупповая дисперсия:
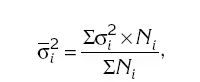
где N i – число единиц в группе.
Межгрупповая дисперсия (S 2) определяет возникающие под влиянием признака-фактора различия в величине исследуемого признака (системную вариацию):
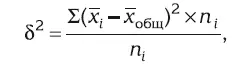
где 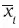 – средняя величина по отдельной группе.
– средняя величина по отдельной группе.
Правило (закон) сложения дисперсий: сумма средней внутригрупповой дисперсии и межгрупповой дисперсии равна общей дисперсии:
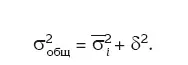
Общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, появляющихся под влиянием положенного в основу группировки признака-фактора и других факторов.
3. Как следствие правила сложения дисперсий появляется возможность определить часть общей дисперсии, находящейся под влиянием положенного в основу группировки признака-фактора.
Среднее квадратическое отклонение (с) – корень квадратный, извлеченный из дисперсии.
Различают простое и взвешенное среднее квадратические отклонения.
Простое (невзвешенное) среднее квадратическое отклонение :
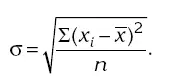
Взвешенное среднее квадратическое отклонение:
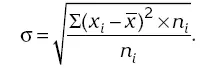
11. Понятие и классификация индексов
1. Индексы относят к важнейшим обобщающим показателям.
 Индекс(лат. index – показатель, указатель, опись, реестр) – относительный показатель, выражающий соотношение значений признака изучаемого явления во времени, в пространстве или сравнение фактических данных с данными, принятыми за основу для сравнения.
Индекс(лат. index – показатель, указатель, опись, реестр) – относительный показатель, выражающий соотношение значений признака изучаемого явления во времени, в пространстве или сравнение фактических данных с данными, принятыми за основу для сравнения.
Основные обозначения индексов:
✓ i – индивидуальные (частные) индексы;
✓ I – общие индексы;
✓ знак внизу справа 0 – базисный период;
✓ знак внизу справа 1 – отчетный период.
Использование символов для обозначения индексируемых показателей:
✓ q – количество (объем) товара в натуральном выражении;
✓ p – цена единицы товара;
✓ z – себестоимость единицы продукции;
✓ ω – выработка продукции в стоимостном выражении (на одного рабочего или в единицу времени);
✓ υ – выработка продукции в натуральном выражении (на одного рабочего или в единицу времени);
Читать дальшеИнтервал:
Закладка:










