А. Красько - Схемотехника аналоговых электронных устройств
- Название:Схемотехника аналоговых электронных устройств
- Автор:
- Жанр:
- Издательство:Томский государственный университет систем управления и радиоэлектроники
- Год:2005
- Город:Томск
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
А. Красько - Схемотехника аналоговых электронных устройств краткое содержание
В учебном пособии рассмотрены теоретические основы и принципы действия аналоговых устройств на биполярных и полевых транзисторах. Анализируются основные схемы, используемые в аналоговых трактах типовой радиоэлектронной аппаратуры, приводятся расчетные формулы, позволяющие определить элементы принципиальных схем этих устройств по требуемому виду частотных, фазовых и переходных характеристик. Излагаются основы построения различных функциональных устройств на основе операционных усилителей. Рассмотрены так же ряд специальных вопросов с которыми приходится сталкиваться разработчикам аналоговых электронных устройств – оценка нелинейных искажений, анализ устойчивости, чувствительности и др.
Пособие предназначено для студентов, обучающихся по направлениям подготовки 552500, 654200 – «Радиотехника», 654100 – «Электроника и микроэлектроника», и может быть полезно для преподавателей и научных работников.
Схемотехника аналоговых электронных устройств - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
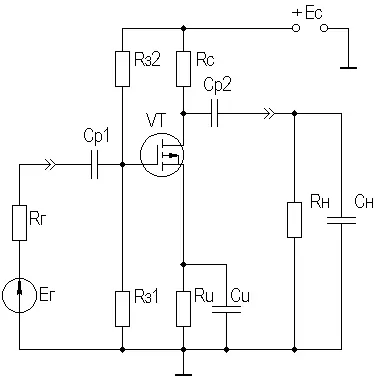
Рисунок 2.34. Схема питания ПТ с делителем в цепи затвора
В [1] приведен ряд полезных практических соотношений:
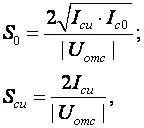
где соответствующие токи показаны на рисунке 2.33, а S си — крутизна при токе стока равном I си .
В ПТ температурная нестабильность тока стока обусловлена следующими факторами (при росте температуры):
◆ увеличением тока стока за счет теплового смещения проходных характеристик (как и в БТ) при малых значениях тока покоя стока I с 0;
◆ уменьшением тока стока за счет удельного сопротивления канала в широком диапазоне изменения тока покоя стока I с 0.
Следовательно, у некоторых типов ПТ возможно существование термостабильной точки покоя (рисунок 2.35).
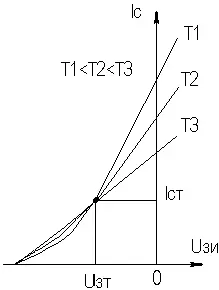
Рисунок 2.35. Температурная зависимость тока стока
Координаты термостабильной точки и соответствующую им крутизну можно приближенно оценить по следующим соотношениям [1]:
U зT ≈ U отс – 0,63 В;
I сT = 0,4· I си / U ² отс≈ (0,1…0,6) мА;
S 0 T ≈ I сT /0,32.
Поскольку ток I сT относительно мал, можно сделать вывод, что широком диапазоне изменений тока стока последний уменьшается с ростом температуры.
Рассмотренные основные схемы питания ПТ осуществляют термостабилизацию режима за счет ООС (последовательной по постоянному току) аналогично каскаду на БТ, т.е. уход тока стока уменьшается в (1 + S 0 R и ) раз. Собственно Δ I с 0 определяется по справочным данным, составляющую теплового смещения проходных характеристик можно определить по аналогии с БТ. Отрицательная температурная зависимость тока стока ПТ может быть использована в целях термокомпенсации каскадов на БТ.
2.11. Усилительный каскад на полевом транзисторе с ОС
Вариант схемы каскада с ОС с автосмещением приведен на рисунке 2.36, схемы для областей СЧ,ВЧ и НЧ приведены, соответственно, на рисунках 2.37а,б,в.
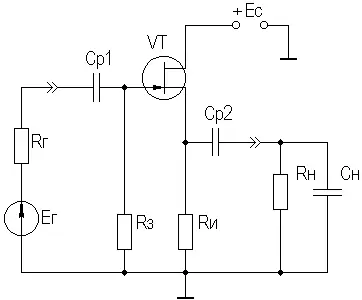
Рисунок 2.36. Усилительный каскад с ОС
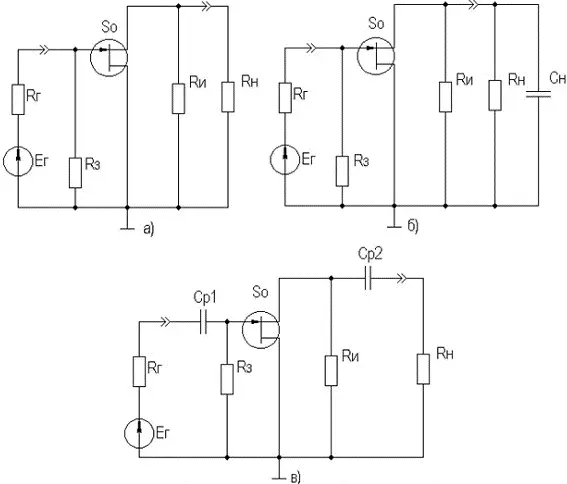
Рисунок 2.37. Схемы каскада с ОС для СЧ, ВЧ и НЧ
Каскад с ОС называют еще "истоковым повторителем" или "повторителем напряжения, т.к., аналогично каскаду с ОК, можно показать, что коэффициент передачи по напряжению этого каскада меньше единицы, и что каскад с ОС не инвертирует фазу входного сигнала.
Графический анализ работы усилительного каскада с ОС проводится как для ОЭ (см. раздел 2.5).
Для расчета параметров каскада с ОС по переменному току используем методику раздела 2.3, а ПТ представлять моделью предложенной в разделе 2.4.2.
Проведя анализ, получим для области СЧ :
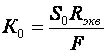 ,
,
где R экв = R и ∥ R н , F = 1 + S 0 R экв — глубина ООС;
R вх ≈ R з ,
R вых = R и ∥ R вых T ,
где R вых T — выходное сопротивление собственно транзистора, R вых T ≈ 1/ S 0.
В целом
R вых T ≈ 1/ S 0,
потому, что, как правило, R и >> 1/ S 0.
В области ВЧ получим:
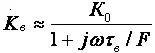
где τ в — постоянная времени каскада в области ВЧ, определяемая аналогично ОИ;
Y вх ≈ 1/ R з + jωC вх дин ,
где C вх дин = C зи + C н ·( K 0+ 1);
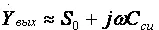
Выражения для относительного коэффициента передачи Y в и коэффициента частотных искажений M в и соотношения для построения АЧХ и ФЧХ каскада с ОК аналогичны приведенным в разделе 2.5 для каскада с ОЭ.
В области НЧ получим:
K н = K 0/(1 + 1/ jωτ н ),
где τ н — постоянная времени разделительной цепи в области НЧ. далее все так же, как для каскада с ОИ.
Усилительный каскад с ОЗ (рисунок 2.38) на практике используется редко, поэтому отдельно рассматриваться не будет. Отметим только, входное сопротивление каскада определяется аналогично выходному для истокового повторителя (≈1/ S 0), а остальные параметры — аналогично ОИ.
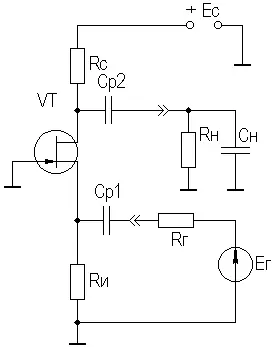
Рисунок 2.38. Усилительный каскад с ОЭ
Характеристики ПТ при различных схемах включения приведены в таблице 2.2.
Таблица 2.2
Характеристики ПТ при различных схемах включения
| Параметр | Схема | ||
|---|---|---|---|
| ОИ | ОЗ | ОС | |
| R вх | Единицы МОм | Единицы, десятки Ом | Единицы МОм |
| R вых | Единицы кОм | Единицы кОм | Единицы, десятки Ом |
| K U | >>1 | >>1 | <1 |
| KI | — | ≅1 | — |
2.12. Временные характеристики усилительных каскадов
2.12.1. Метод анализа импульсных искажений
Рассмотренные усилительные каскады могут быть использованы для усиления импульсных сигналов. Для оценки искажений формы усиливаемых импульсных сигналов необходимо рассмотреть переходные процессы в усилительных каскадах. При анализе переходных процессов будем считать каскады линейными, т.е. амплитуда сигналов в них существенно меньше постоянных составляющих токов и напряжений в рабочей точке. В этом случае наиболее удобным методом анализа является преобразование Лапласа (операторный метод).
Временной процесс в электрической цепи описывается системой интегро-дифференциальных уравнений (СИДУ). Применяя прямое преобразование Лапласа (ППЛ), приводят СИДУ к системе линейных алгебраических уравнений (СЛАУ), которая просто решается относительно некоторой промежуточной функции, по которой с помощью обратного преобразования Лапласа (ОПЛ) находится решение для исходной СИДУ.
ППЛ функции вещественного переменного f(t)("оригинала") служит для нахождения преобразованной функции f(p)("изображения") и определяется соотношением:
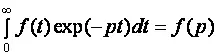
ОПЛ определяется формулой:
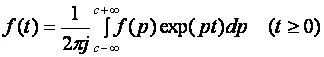
где p = α + j ω.
Читать дальшеИнтервал:
Закладка:










