А. Красько - Схемотехника аналоговых электронных устройств

Выражение для относительного коэффициента передачи усилительных каскадов на БТ и ПТ в области НЧ имеет вид:

Y н ( jω ) = jω н /(1 + jωτ н ).

Получим выражение для переходной характеристики:

h н ( p ) = Y н ( p )/ p = τ н /(1 + pτ н ).

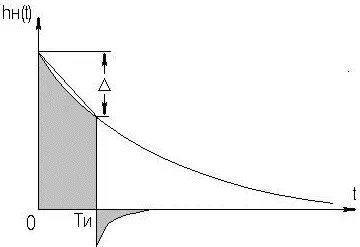
Рисунок 2.40. Переходный процесс в области БВ

По таблице 2.3 получим "оригинал":

h н ( t ) = –exp(– t / τ н ).

При T и ≤ τ н , разлагая h н ( t ) в степенной ряд и ограничившись двумя членами, при t = T и (рисунок 2.40) получаем для случая малых искажений плоской вершины импульса (Δ≤20%):

h н ( t ) = –exp(– t / τ н ) ≈ 1 – T и / τ н = 1 – Δ,

откуда:

Δ = T и / τ н .

Т.к. временные и частотные характеристики каскадов выражаются через постоянные времени τ в и τ н , то легко получить связывающие их выражения. Итак:

f в = 1/2π τ в ,

f н = 1/2π τ н ,

t у = 2,2· τ в ,

Δ = T и / τ н .

откуда при M в = M н = 3 дБ получаем:

f в = 2,2/2π τ в = 0 ,35 t у ,

f н = Δ/2π τ нT и .

Целью коррекции является расширение диапазона рабочих частот, как в области ВЧ, так и в области НЧ в усилителях гармонических сигналов, либо уменьшение искажений в областях МВ и БВ в усилителях импульсных сигналов.

В области ВЧ (МВ) применяется простая параллельная индуктивная коррекция. Более сложные варианты индуктивной коррекции применяются редко из-за сложности настройки и трудности при реализации УУ в микроисполнении.

Схема каскада с простой параллельной индуктивной ВЧ-коррекцией на ПТ со схемой для области ВЧ (МВ) приведены на рисунке 2.41.

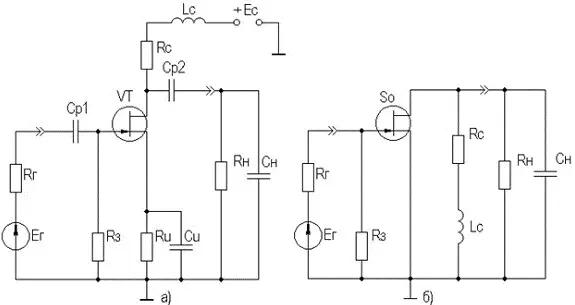
Рисунок 2.41. Каскад на ПТ с простой параллельной коррекцией

Физически эффект увеличения f в объясняется относительным увеличением коэффициента передачи на ВЧ за счет увеличения эквивалентной нагрузки каскада (путем добавления индуктивного сопротивления Z Lс в цепь стока). Эффект уменьшения t у объясняется увеличением тока через емкость C н (что сокращает время ее заряда и, следовательно, уменьшает t у ) за счет того, что в начальный момент выходной ток транзистора практически весь направляется в цепь R нC н , его ответвлению в стоковую цепь препятствует ЭДС самоиндукции в индуктивности L с .

В [6] приводятся основные выражения для расчета каскадов с простой индуктивной параллельной ВЧ коррекцией для случая, когда R н >> R с , что практически всегда имеет место в промежуточных каскадах на ПТ:

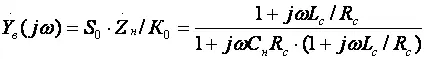
После преобразования получаем:

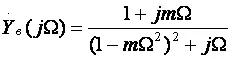
где Ω — нормированная частота, Ω = ωτ в , τ в = R сC н ;

m — коэффициент коррекции, по физическому смыслу представляющий собой квадрат добротности ( Q к ) параллельного колебательного контура L сR сC нR н (см. рисунок 2.41б), m ≈ L с /( C нR н ²)= Q к ².

Модуль полученного выражения дает АЧХ корректированного каскада:

Максимально плоская АЧХ получается, когда m=0,414 [6]. Данное условие вытекает из равенства нулю производной Y в (Ω) при Ω=0, т.е. АЧХ не должна иметь наклона в точке W=0.

ФЧХ корректированного каскада определяется выражением:

φ в = arctg[( m – 1)Ω – m ²Ω³].

ФЧХ максимально линейна, если m=0,322 [6]. Добротность Q к =0,5 соответствует границе между апериодическими и колебательными разрядами конденсатора контура L сR сC нR н , поэтому при m≤0,25 выброса в ПХ не будет, т.к. не будет затухающих колебаний в контуре.

На рисунке 2.42 приведены нормированные АЧХ и ПХ каскадов на ПТ с простой параллельной индуктивной коррекцией для различных коэффициентов коррекции m.

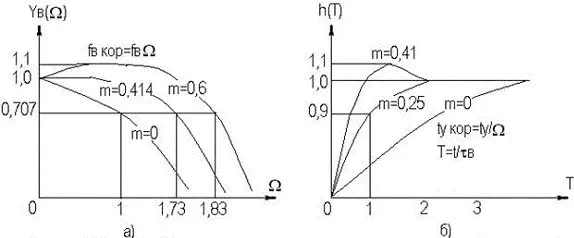
Рисунок 2.42. АЧХ и ПХ каскадов с простой параллельной индуктивной коррекцией

Для оценки эффективности УУ вводят понятие площади усиления П для ШУ и импульсной добротности D для ИУ:

Π = K 0· f в ,

D = K 0/ t у ,

Π = 0,35· D .

Как видно из рисунка 2.42, максимальный выигрыш по этим параметрам в каскаде на ПТ для рассмотренного варианта коррекции и отсутствии подъема АЧХ на ВЧ (выброса ПХ в области МВ), составляет 1,73 [6] раза. Следует подчеркнуть, что данный выигрыш получается при условии когда R н >> R с , что обычно имеет место при использовании каскада на ПТ в качестве промежуточного в УУ.

В каскадах на БТ (схема не приводится ввиду ее подобия рисунку 2.41) анализ эффективности простой параллельной индуктивной коррекции сложнее из-за необходимости учета частотной зависимости крутизны БТ, .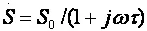

Выражение для относительного коэффициента передачи имеет вид [6]:

здесь τ в =τ+τ 1+τ 2 — постоянная времени каскада без коррекции на ВЧ; m = L с ( R к · τ в ) — коэффициент коррекции; х =(τ+τ 1)/ τ в — отношение составляющих постоянной времени каскада.

Данное выражение не позволяет однозначно оценить выигрыш, даваемый простой параллельной индуктивной коррекцией в каскадах на БТ, поэтому либо приходится прибегать к помощи ЭВМ, либо пользоваться таблицами, приведенными, например, в [6]. Анализ показывает, что выигрыш в площади усиления (импульсной добротности) может достигать величины, равной 0,5 S 0 r б , т.е. величины, большей двух раз (теоретически до 20, практически 2…10).

Анализ так же показывает, что простая параллельная индуктивная коррекция в каскаде на БТ наиболее эффективна при малых х, что соответствует случаю применения относительно низкочастотных транзисторов.

В целом же следует заметить, что, несмотря на некоторую эффективность, простая параллельная индуктивная коррекция в современной схемотехнике УУ используется редко. Это объясняется, в первую очередь, технологическими трудностям реализации индуктивностей в ИМС, и сильной зависимостью эффекта коррекции от параметров транзистора, что требует подстройки схемы в случае их разброса. Возможно использование вместо катушки индуктивности индуктивного входного сопротивления каскада с ОБ (рисунок 2.43).