А. Красько - Схемотехника аналоговых электронных устройств

Необходимость расчета функции чувствительности возникает при необходимости учета влияния на характеристики АЭУ факторов окружающей среды (температуры, радиации и т.д.), при расчете требуемых допусков на параметры компонент, при определении процента выхода ИМС, в задачах оптимизации, моделирования и т.д.

Функция чувствительности S i параметра устройства yк изменению параметра компонента x i определяется как частная производная

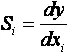
Данное выражение получено на основе разложения в ряд Тейлора функции нескольких переменных 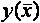, где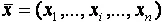

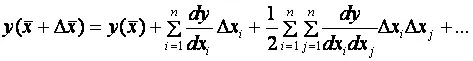
Пренебрегая частными производными второго и более порядка, получаем связь функции чувствительности и отклонения параметра :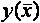

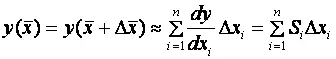
Существуют разновидности функции чувствительности:

◆ абсолютная чувствительность 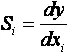, абсолютное отклонение при этом равно ;

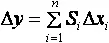◆ относительная чувствительность 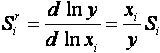, относительное отклонение равно ;

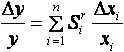◆ полуотносительные чувствительности , .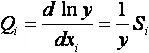

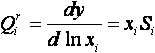Выбор вида функции чувствительности определяется видом решаемой задачи, например, для комплексного коэффициента передачи 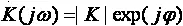относительная чувствительность равна относительной чувствительности модуля (действительная часть) и полуотносительной чувствительности фазы (мнимая часть):

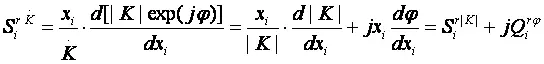
Для простых схем вычисление функции чувствительности может осуществляться прямым дифференцированием схемной функции, представленной в аналитическом виде. Для сложных схем, получение аналитического выражения схемной функции представляет собой сложную задачу, возможно применение прямого расчета функции чувствительности через приращения. В этом случае необходимо проводить n анализов схемы, что для сложных схем весьма нерационально.

Существует косвенный метод расчета чувствительности по передаточным функциям, предложенный Быховским [17]. Согласно этому методу, функция чувствительности, например, прямого коэффициента передачи равна произведению функций передачи с входа схемы до элемента, относительно которого ищется чувствительность, и передаточной функции "элемент — выход схемы" (рисунок 8.4а).

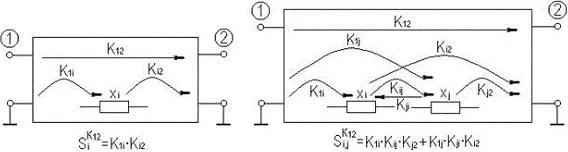
Рисунок 8.4. Косвенный метод расчёта функций чувствительности

Так как расчет функции чувствительности сводится к расчету передаточных функций, то для их нахождения возможно применение, например, обобщенного метода узловых потенциалов. Косвенный метод расчета по передаточным функциям позволяет находить функции чувствительности более высоких порядков. На рисунке 8.4б проиллюстрировано нахождение функции чувствительности второго порядка. В общем же существует n! путей передачи сигнала, каждый из которых содержит n+1 сомножителей.

Ниже описывается метод расчета функции чувствительности, сочетающий прямой метод дифференцирования и косвенный по передаточным функциям, позволяющий за один анализ находить чувствительность к n элементам схемы [18]. Рассмотрим данный способ на примерах получения выражений для абсолютной чувствительности первого порядка S-параметров электронных схем, описанных матрицей проводимости [Y].

В матричном представлении характеристики электронных схем, в том числе и параметры рассеяния [S], определяются в виде отношений алгебраических дополнений матрицы [Y] (см. подраздел 7.2). Изменяемый параметр входит при этом в некоторые элементы алгебраических дополнений. Определение функции чувствительности сводится в этом случае к нахождению производных от отношений алгебраических дополнений (или алгебраических дополнений и определителя) по элементам, в которых содержится изменяемый параметр. В случае, когда изменяемый параметр входит в элементы дополнений определителя функционально, чувствительность определяется как сложная производная.

Для определения производных алгебраических дополнений по изменяемым параметрам входящих в них элементов воспользуемся теоремой, утверждающей, что производная определителя по какому-либо элементу равна алгебраическому дополнению этого элемента. Доказательство теоремы основано на разложении определителя по Лапласу

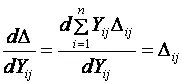
Общее выражение для S-параметров через алгебраические дополнения имеет вид (см. подраздел 7.2)

S ij = k ij Δ ji /Δ – δ ij .

Определим функции чувствительности параметров рассеяния к пассивному двухполюснику y o включенному между произвольными узлами k и l (см. рисунок 8.5а)

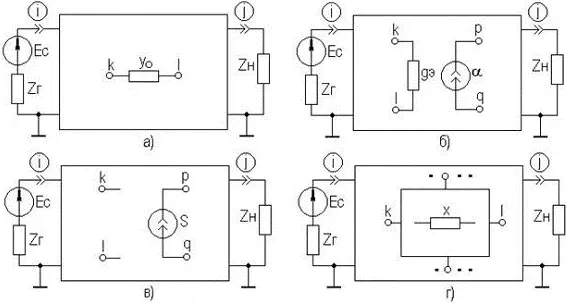
Рисунок 8.5. Расчёт чувствительности S-параметров

S S ij y 0= dS ij / dy 0= k ij (Δ ji ( k + l )( k + l )Δ – Δ ( k + l )( k + l )Δ ji )/Δ² = – k ij Δ j ( k + l )Δ ( k + l ) i /Δ² = – k ij [(Δ jk – Δ jl )(Δ ki – Δ li )]/Δ²

При получении данного и последующих выражений используются следующие матричные соотношения [3]: