А. Красько - Схемотехника аналоговых электронных устройств

В практическом плане чаще всего используется модификация табличного метода — модифицированный узловой метод с проверкой [4].

Идея данного метода заключается в разделении элементов на группы; одна группа сформирована из элементов, которые описываются помощью проводимостей, для элементов второй группы такое описание невозможно. Поскольку через токи ветвей первой группы можно выразить напряжения ветвей, а напряжения ветвей через узловые потенциалы, то можно исключить из табличных уравнений все напряжения ветвей, а для элементов первой группы еще и токи ветвей. При введении дополнительных уравнений для токов в ветвях с элементами второй группы производится проверка на наличие заранее известных (нулевых) переменных. В результате такого преобразования получим уравнения модифицированного узлового метода с проверкой

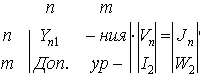
или в общем виде

T mX=W,

где n — размерность матрицы проводимости Y n 1 элементов первой группы (n — число узлов схемы без нулевого); m — число дополнительных уравнений для элементов второй группы; J n — вектор независимых источников тока; I 2 — вектор токов ветвей элементов второй группы; W 2 — вектор, куда входят независимые источники напряжения, а также начальные напряжения и токи на конденсаторах и индуктивностях, представленных элементами второй группы.

Для упрощения программирования обычно представляют матрицу коэффициентов системы уравнений модифицированного узлового метода T m в виде суммы двух матриц размерностью (n+m)*(n+m)

T m= G + pC .

В матрицу Gвносят все активные проводимости и коэффициенты, соответствующие частотно-независимым элементам, а в матрицу C — все частотнозависимые элементы, причем индуктивности обычно представляют элементом второй группы, т.е. сопротивлением. Далее находят решение данной системы уравнений, используя алгоритмы Гаусса-Жордана либо L/U-разложения [4].

При частотном анализе электронных схем оператор pзаменяется на jω, организуется цикл по частоте, внутри которого для каждой частотной точки формируется система уравнений, которая решается относительно интересующих напряжений и токов.

При временном анализе линейных электронных схем возможно непосредственно использовать модифицированную узловую форму уравнений

( G + pC ) X = W .

После перехода во временную область получим

Gx + Cx' = W ,

или

Cx' = W – Gx .

Решение полученной системы дифференциальных уравнений находится путем численного интегрирования. Одними из эффективных методов численного интегрирования являются методы, опирающиеся на линейные многошаговые формулы [4], к простейшим из которых относятся формулы Эйлера (прямая и обратная) и формула трапеций.

Разбив временной интервал [0,T] на конечное число отрезков h и положив t n +1 =t n+h , для каждого момента времени t n можно найти приближение x n к истинному решению x ( t n ) путем применения линейных многошаговых формул:

x n +1 = x n+ hx' n (прямая формула Эйлера);

x n +1 = x n+ hx' n +1 (обратная формула Эйлера);

x n +1 = x n + ( h /2)( x' n + x' n +1) (формула трапеций).

Нахождение x' n +1 для (n+1)-го шага вычислений возможно путем применения прямой формулы Эйлера.

Поскольку напряжение на конденсаторе и ток, протекающий через него связаны соотношением i=CdV/dt, а для индуктивности имеем V=Ldi/dt, то применение обратной формулы Эйлера равноценно переходу от емкостей и индуктивностей к их эквивалентным схемам, показанным на рисунке 8.6, в результате чего цепь становится резистивной. Такие модели индуктивности и емкости носят название сеточных (сопровождающих, дискретных) моделей .

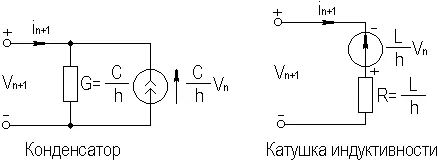
Рисунок 8.6. Сеточные модели для обратной формулы Эйлера

Отыскание рабочей точки или расчет по постоянному току является первым шагом при нелинейном анализе УУ. Анализ характеристик по постоянному току схем, содержащих нелинейные сопротивления, сводится к решению системы нелинейных уравнений вида f(x)=0.

Поскольку законы Кирхгофа применимы не только к линейным, но и к нелинейным элементам, для формирования системы уравнений f(x)возможно использование уже рассмотренных табличных методов. Структура получаемых табличных уравнений будет рассмотрена ниже.

Для решения системы нелинейных уравнений f(x)применяется метод Ньютона-Рафсона [4]. Метод предусматривает использование начального приближения x 0, проведение итерационной процедуры и, если величина |( x n +1– x n )/ x n +1| достаточно мала, констатацию факта сходимости (n- количество итераций):

x n +1= x n – J -1 f ( x n ),

где J —якобиан (матрица Якоби) размерностью (m*m)

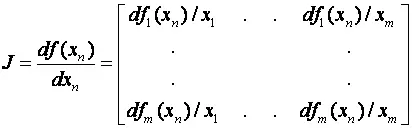
В процессе итерационной обработки данной системы уравнений на каждом этапе итерации могут быть получены значения f ( x n ) и J; это эквивалентно решению линейного уравнения в форме

J ( x n +1) – x n ) = – f ( x n ).

Другими словами, решение нелинейных уравнений можно интерпретировать как повторное решение линейных уравнений на каждом этапе итерационного процесса.

Структура якобиана внешне совпадает с табличными уравнениями линейных цепей, которые преобразованы с учетом расчета по постоянному току — убраны конденсаторы и закорочены катушки индуктивности.

Пусть табличные уравнения заданы в следующей форме:

V в – A tV п = 0;

p ( V в , i в ) = W ;

AI в = 0;

Система уравнений p ( V в , i в ) = W определяет связь между токами и напряжениями ветвей в неявной форме, некоторые из этих зависимостей могут быть линейными.

Матрица Якоби на n-й итерации будет иметь вид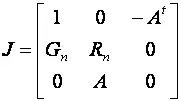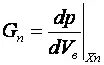

где ; где .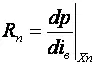

Для формирования якобиана возможно использование различных модификаций табличного метода, в том числе и модифицированного узлового с проверкой. Результат анализа схемы по постоянному току (режим по постоянному току) может быть использован в качестве начального приближения при временном анализе нелинейных электронных схем.