Тим Саттон - Краткое введение в ГИС

Топология — это сложное представление векторных данных. Топологические наборы данных хранятся в специальных файловых форматах, включающих описание отношений между объектами. В то же время, наиболее распространенные форматы геоданных являются «простыми», то есть хранят только геометрию и атрибуты. Они разработаны для быстрого отображения на карте и не расчитаны на топологический анализ (например, поиск кратчайшего пути). Многие ГИС-приложения могут отображать и топологические и простые данные, а некоторые могут также создавать и редактировать эти данные.

Закрепим изученный материал:

• Топологияописывает пространственные взаимоотношения соседствующих векторных объектов.

•В ГИС-приложениях за топологию отвечают топологические инструменты.

•Топологию можно использовать для выявления и исправления ошибок, возникших в ходе оцифровки.

•Корректная топология необходима для некоторых видов анализа, таких как сетевой анализ.

•Установка радиуса замыканияи радиуса поискапомогает нам производить топологически корректную оцифровку.

• Простые векторные данныене включают топологические правила, но они широко используются в ГИС-приложениях.

Ниже приведено несколько примеров практических заданий для Ваших учеников:

•Отметьте автобусные остановки на листе топографической карты и попросите учеников найти кратчайший маршрут между двумя остановками.

•Подумайте, как бы Вы создали векторные объекты в ГИС для представления топологической сети дорог в Вашем городе. Какие топологические правила важны в данном случае и какие инструменты QGIS могут использовать ученики, чтобы проверить топологическую корректность созданного набора данных?

Вы можете использовать карту автобусных или ж/д маршрутов и обсудить пространственные отношения и топологию с учениками.

Книги:

•Сhang, Kang-Tsung (2006): Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. (ISBN 0070658986)

•DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. (ISBN 9814126195)

Веб-сайты:

http://www.innovativegis.com/basis/primer/concepts.html

http://en.wikipedia.org/wiki/Geospatial_topology

Руководство Пользователя QGIS включает более детальную информацию о топологическом редактировании.

В следующем разделе мы изучим системы координат, чтобы понять, как географические данные о шарообразной Земле переносятся на плоские карты.

Цель:Понимание систем координат

Ключевые слова:Система координат (СК), Картографическая Проекция, Проецирование «На лету», Широта, Долгота, Северное Смещение, Восточное Смещение

Картографические проекциислужат для представления сферической поверхности Земли на плоскости бумажной или компьютерной карты. Системы координат(СК) определяют, как двумерная спроецированная карта описывает реальные местоположения объектов на Земле с помощью координат. Выбор картографической проекции и системы координат зависит от географической области, которую Вы хотите показать на карте, от задач, стоящих перед будущей картой, и часто от доступности данных.

Традиционный метод представления формы Земли — это глобус. Тем не менее, здесь возникает ряд проблем. Хотя глобусы достаточно точно передают форму Земли и очертания континентов, их невозможно носить с собой в кармане. Также они подходят для использования в очень малых масштабах (примерно 1 к 100 млн). Большинство тематических данных, используемых в картографических приложениях, имеют гораздо более крупный масштаб. Типичные наборы геоданных имеют масштаб 1:200 000 или крупнее, в зависимости от уровня детализации. Глобус подобного масштаба было бы трудно произвести и еще более трудно сдвинуть с места. Поэтому картографы разработали ряд математических техник, называемых картографическими проекциями, разработанных для представления сферической поверхности Земли в двух измерениях.

Смотря на Землю с близкого расстояния, люди воспринимают ее плоской. Тем не менее, из космоса она выглядит шарообразной. Карты, как известно, являются представлением реальности. Они создаются для представления не только самих объектов, но и их формы, размеров и пространственных отношений. Каждая картографическая проекция имеет достоинстваи недостатки. Выбор лучшей проекции зависит от масштабакарты и от цели ее создания. Например, проекция, которая будет иметь неприемлемые искажения в случае создания карты на весь африканский континент, может быть отличным решением для составления крупномасштабной (детальной) картыодного из африканских городов. Свойства картографической проекции также воздействуют на визуальные характеристики карты. Некоторые проекции хороши для малых областей, некоторые — для территорий с большим протяжением с запада на восток, третьи — с севера на юг.

Процесс создания картографической проекции может быть наглядно показан путем помещения источника света внутрь прозрачного глобуса с обозначенными параллелями и меридианами. Свет падает на лист бумаги. Различные способы проецирования имитируются оборачиванием глобуса листом в форме цилиндра, конуса, или просто прикладыванием плоскоголиста. Каждый из этих методов называется семейством картографических проекций. Таким образом, существуют семейства цилиндрических, коническихи плоскостных проекций(см. Рисунок 62 а, б, в).

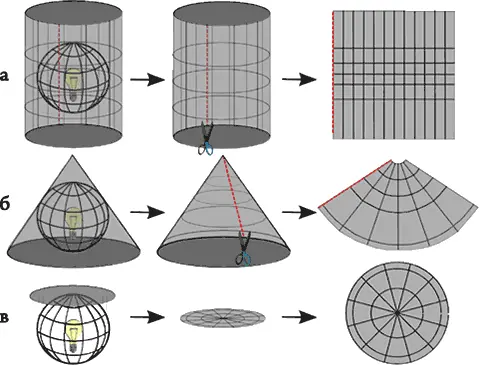
Процесс проецирования осуществляется с использованием математических принципов геометрии и тригонометрии. Процесс, показанный выше, моделируется числовыми функциями.

Картографические проекции по определению не могут передать сферическую поверхность со 100% точностью. В ходе проецирования любая карта будет иметь искажения углов, расстоянийили площадей. Картографическая проекция может быть компромиссной, т. е. искажать все три свойства в некоторых допустимых пределах. Примером компромиссной проекции служит проекция Робинсона(см. Рисунок 63), часто используемая для карт мира.