Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Response to Unit Step Function

vs i 0 PWL (0,0 1us ,1V 5s, 1V)

С 2 3 0.125

R 2 3 2

R1 2 0 1

X 2 1 3 iop

.subckt iop m p v0

ri m p 1meg

e v0 0 p m 2e5

.ends

.TRAN 0.05s 3s

.PROBE

.END

После запуска анализа в программе Probe используем курсор, чтобы убедиться, что при t =0,5 с, V 0=2,73 В. Это соответствует значению, вычисленному из приведенного выше уравнения. Результаты анализа приведены на рис. 5.21.

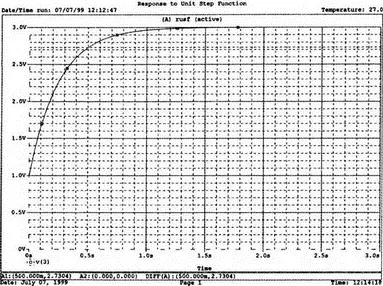
Рис. 5.21. Результат анализа схемы на рис. 5.20, а

Когда в схеме имеется несколько однотипных устройств, намного проще работать, представив их в виде подсхем. Предположим, что мы собираемся сравнить частотные характеристики для двух ОУ, схемы которых мы предварительно рассмотрели (в разделе «Амплитудно-частотные характеристики операционного усилителя»). Вспомним, что схемы были подобны за исключением того, что в первом случае R 2=240 Ом, а во втором случае R 2=15 Ом. Их частотные характеристики удобнее сравнивать на общем графике.

Чтобы добиться этого, схему просто расширяют так, чтобы оба случая были исследованы одновременно. Мы определим ОУ подсхемой и используем рис. 5.22, чтобы обеспечить простую идентификацию узлов. Усилители Ор1 и Ор2 показаны просто в виде треугольников, поскольку вы уже знакомы с их моделью, нет необходимости повторять внутренние подробности. Теперь легко получить входной файл:

Double Op Amp Circuit for Gain-Bandwidth Analysis

VS1 2 0 AC 1raV

R1 1 0 10k

R2 3 1 240k

X1 1 2 3 opamp

VS2 5 0 AC 1mV

R3 4 0 10k

R4 6 4 15k

X2 4 5 6 OPAMP

.AC DEC 40 100 10MEG

.PROBE

.subckt opamp m p vo

eg a 0 p m 1e5

e с 0 b 0 1

rin m p 1meg

ri1 a b 1k

с b 0 15.92uf

ro1 с vo 50

.ends

.END

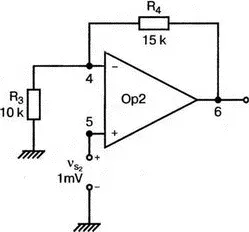
Рис. 5.22. Схема с двумя ОУ

Подсхема описывается так же, как и прежде. После создания подсхемы вы можете просто скопировать ее в любой входной файл, где она необходима. В данном случае она вызывается дважды — сначала командой X1 , а затем командой X2. Список узлов, используемых в каждом случае, такой же, как на рис. 5.22.

Выполните анализ и затем получите графики

20·lg(V(3)/V(2)),

и

20·lg(V(6)/V(5)).

Используйте режим курсора, чтобы найти отметку 3 дБ для первого графика. Обратите внимание, что при включении режима курсора автоматически выбирается первый график. Убедитесь, что А mid =27,96 дБ и f 3дБ=39,4 кГц.

Исследуйте теперь второй график. Нажмите Ctrl и → (стрелку вправо), чтобы перевести курсор на второй график. Затем двигайтесь по второму графику, пока не достигнете нужной точки. Обратите внимание, что второй график показывает А mid =7,96 дБ, что на 20 дБ меньше, чем у первого. Искомая частота будет соответствовать коэффициенту усиления 4,96 дБ (7,96–3,00). Убедитесь, что это дает f 3дБ=394 кГц. Эти результаты соответствуют полученным в предыдущих примерах. Сравните полученный вами двойной график с рис. 5.23.

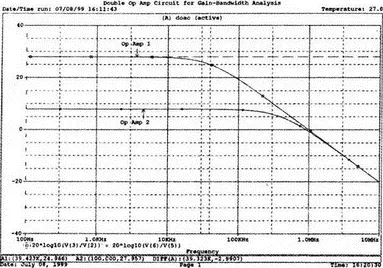
Рис. 5.23. Результат анализа схемы с двумя ОУ

Для получения более крутых границ полосы пропускания, чем у простых однополюсных фильтров, содержащих, например, только один конденсатор, могут применяться высокочастотные, низкочастотные и полосовые активные фильтры. Классическим примером таких устройств являются фильтры Баттерворта.

ОУ часто используются при разработке активных фильтров, поскольку получить усилители с высокими добротностями на базе ОУ достаточно просто. Мы не будем касаться теории фильтров в нашем обсуждении. Если вы изучаете активные фильтры впервые, обратитесь к другим источникам, чтобы лучше оценить элегантность и простоту этих схем.

Воспользуемся таблицами нормированных многочленов Баттерворта, чтобы найти коэффициенты для фильтра второго порядка:

s ² + 1,414 s + 1.

Фильтр второго порядка показан на рис. 5.24. Для вводного примера найдем элементы R 1, R 2, R и С для фильтра Баттерворта с частотой среза f c= 5 кГц. Как обычно, в качестве частоты среза принимается частота, при которой характеристика снижается на 3 дБ. Согласно теории, низкочастотный коэффициент усиления задается выражением:

A vo = 3 – 2 k,

где k представляет собой коэффициент затухания, определенный как половина коэффициента при s ² из таблицы полиномов Баттерворта (см. Hillburn and Johnson. Manual of Active Filter Designs, McGraw-Hill, 1973). Для этого примера k =0,707 и

A v0= 3 - 1,414 = 1,586.

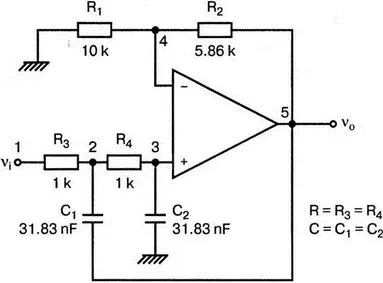
Рис. 5.24. Низкочастотный фильтр Баттерворта второго порядка

Допустим, что R 1=10 кОм. Из выражения

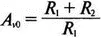
получаем R 2=5,86 кОм. Если положить R= 1 кОм, из выражения f c =1/(2π RC ) найдем С =31,83 нФ. Чтобы проверить теорию Баттерворта, используем идеальную модель ОУ в качестве подсхемы, как показано на рис. 5.25. Для этого создайте следующий входной файл:

Second-Order Butterworth Filter

V1 1 0 AC 1mV

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 5.86k

C1 2 5 31.83nF

C2 3 0 31.83nF

X 4 3 5 iop

.AC DEC 40 1 100kHz

.PROBE

.subckt iop m p vo

e vo 0 p m 2e5

rin m p 1meg

.ends

.END

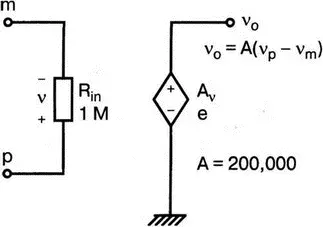
Рис. 5.25. Подсхема для идеального ОУ

Проведите анализ и получите график V(5)V(1). Выясните, что А v0 =1,586, что соответствует нашему расчету. Затем удалите этот график и получите график зависимости

20·lg(V(5)/(V(1)·1,587В)).

Убедитесь, что f c =5 кГц. Этот фильтр второго порядка должен иметь вдвое большую крутизну спада, чем фильтр первого порядка. Вспомним, что фильтр первого порядка имеет скорость спада 20 дБ/дек. Убедитесь, что при f =10 кГц A v =12,31 дБ, а при f =100 кГц A v =52,05 дБ, что составляет приблизительно 40 дБ/дек. Этот график показан на рис. 5.26.

Рис. 5.26. График Боде для низкочастотного фильтра Баттерворта второго порядка