Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

В качестве другого примера рассмотрим фильтр Баттерворта четвертого порядка, предназначенный для работы на частоте f c =1 кГц. Из таблицы полиномов находим коэффициенты:

( s ² + 0,765 s + 1)·( s ² + 1,848 s + 1).

Коэффициент затухания k равен половине коэффициента при s в каждом квадратном уравнении, давая k 1=0,383 и k 2=0,924:

A v1= 3 – 2 k 1= 3 – 0,765 = 2,235 и A v2= 3 – 2 k 2= 1,152.

Для первого каскада примем R 1=10 кОм и с помощью уравнения

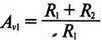
найдем R 2=12,35 кОм. Приняв для второго каскада R 1=10 кОм, получим R 2=1,52 кОм. При f c =1 кГц, если положить R =1 кОм, С =0,16 мкФ. Схема показана на рис. 5.27. Поскольку каждый элемент должен иметь уникальное обозначение, вычисленные здесь значения R и С относятся к соответствующим резисторам и конденсаторам каждого из каскадов. Входной файл при этом:

Fourth-Order Butterworth Filter

V1 1 0 AC 1mV

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 12.35k

R7 5 6 1k

R8 6 7 1k

R5 8 0 10k

R6 9 8 1.52k

C1 2 5 0.16uF

C2 3 0 0.16uF

C3 6 9 0.16uF

C4 7 0 0.16uF

.AC DEC 40 1 10kHz

.PROBE

.subckt iop m p vo

E vc N

i p m 2e5

rin m p 1meg

.ends

X1 4 3 5 iop

X2 8 7 9 iop

.END

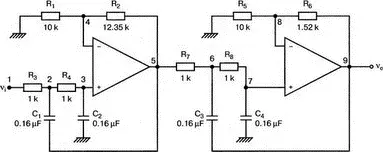
Рис. 5.27. Полосовой фильтр Баттерворта четвертого порядка

Выполните анализ и затем получите совместный график для V(5)/V(1), (V)9/V(5), и V(9)/V(1). Они представляют собой коэффициенты усиления первого и второго каскадов и полный коэффициент усиления соответственно. Так как они выражены не в децибелах, вы легко сможете проверить, что A v1=2,235, A v2 = 1,152, а общий коэффициент усиления A v=A v1· A v2 = 2,575. Вы можете найти эти значения, используя режим курсора при низких частотах. Нажимайте Ctrl и →, чтобы выбрать нужный график. Сравните полученные вами графики с представленными на рис. 5.28.

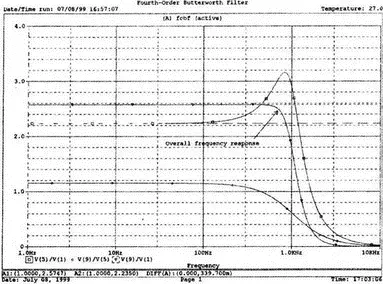
Рис. 5.28. АЧХ фильтра Баттерворта четвертого порядка

Получите распечатку результатов анализа, включая все три графика для дальнейшего изучения. Обратите внимание на интересный пик на графике A v1. Он компенсируется провалом на графике А v2, поэтому график полного коэффициента усиления становится плоским почти на всей полосе пропускания, круто падая при частоте, близкой к 1 кГц.

Крутизну легче определить из графика в децибелах. Используйте характеристику 20·lg(V(9)/V(1)) и так далее, заменив три графика логарифмическими характеристиками. Убедитесь, что для полной схемы, f c =1 кГц. Также пронаблюдайте скорость спада для каждого из трех графиков. Вы сможете показать, что для каждого из двух каскадов, крутизна спада составляет приблизительно 10 дБ/дек по сравнению с приблизительно с 20 дБ/дек для общей характеристики. Разве не вызывает восхищения простота восприятия основных идей при передаче их графическим способом. Вы должны также оценить, сколько времени и усилий сэкономлено при использовании такого мощного вычислительного инструмента, как PSpice. Сравните кривые представленные на рис. 5.29, с полученными графиками.

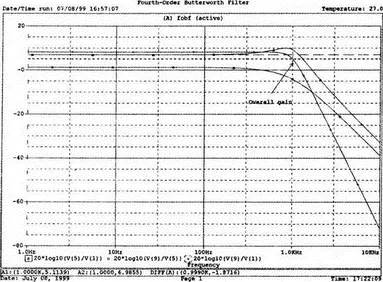
Рис. 5.29. Логарифмические АЧХ (ЛАЧХ) фильтра Баттерворта четвертого порядка

Мы можем показать одно дополнительное свойство фильтра Баттерворта, слегка модифицировав предыдущий входной файл. Сравните фильтры второго и четвертого порядков. Будут необходимы некоторые вычисления, поскольку мы не имеем данных для двухкаскадного фильтра при f =1 кГц.

Низкочастотный коэффициент усиления будет таким же, как вычисленный ранее для фильтра второго порядка, а именно: A v =1,586. Положив R 1=10 кОм, получим R 2=5,86 кОм.

При R =1 кОм найдем, что С= 0,159 мкФ. Дополнение к схеме на рис. 5.27, позволяющее включить в схему фильтр второго порядка, показано на рис. 5.30. Отметим, что это дополнение имеет номера узлов большие, чем приведенные на рис. 5.27. Этот фильтр имеет собственный вход и физически не связан с четырехкаскадным фильтром. Если дополнить входной файл соответствующей информацией, он примет вид:

Fourth-Order Butterworth Filter Compared with Second-Order

VI 1 0 AC 1mv

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 12.35k

R7 5 6 1k

R8 6 7 1k

R5 8 0 10k

R6 9 8 1.52k

C1 2 5 0.16uF

C2 3 0 0.16uF

C3 6 9 0.16uF

C4 7 0 0.16uF

VII 10 1 AC imV

R9 13 0 10k

R10 14 13 5.36k

R11 10 11 1k

R12 11 12 1k

C5 11 14 0.159uF

C6 12 0 0.159uF

X1 4 3 5 iop

X2 8 7 9 iop

X3 13 12 14 iop

.AC DEC 40 1 10kHz

.PROBE

.subckt iop m p vc

VC 0pm 2e5

ein m p 1meg

.ends

.END

Рис. 5.30. Дополнение к схеме на рис. 5.27, позволяющее включить в схему фильтр второго порядка

Выполните анализ и получите графики в децибелах V(9)/V(1) для фильтра четвертого порядка и V(14)/V(10) для фильтра второго порядка. Вы должны получить A v= 4,006 дБ (второй порядок) и A v =8,214 дБ (четвертый порядок). Мы хотим показать их при сравнимой базе, поэтому построим графики

20·lg(V(14)/V(10)),

и

20·lg(V(9)/V(1)) – 4,208.

Значение 4,208 представляет смещение второго графика относительно первого, нормализующего второй график относительно первого. Эти графики (рис. 5.31) с накладывающимися в низкочастотном диапазоне траекториями ясно показывают, что оба фильтра Баттерворта имеют одинаковую частоту f c =1 кГц. Это относится к фильтрам Баттерворта всех порядков.

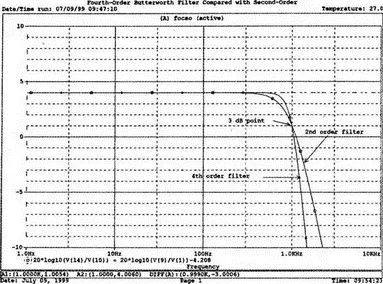
Рис. 5.31. Логарифмических АЧХ для фильтров Баттерворта второго и четвертого порядков

В простой резонансной схеме резонансные свойства RLC -цепи используются для создания крутого спада характеристики на границах полосы пропускания. На рис. 5.32 показан входной колебательный контур, содержащий V s, R, L и C . Выберем параметры элементов, обеспечивающие необходимую ширину полосы частот В и добротность Q .