Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

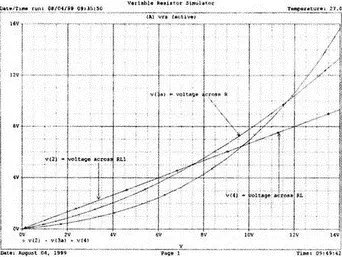
Рис. 13.2. Характеристики вход-выход для модели нелинейного резистора

В любой электрической цепи, через которую проходит ток, возбуждается также и магнитное поле. Величиной, характеризующей магнитное поле и прямо пропорциональной току I , является напряженность магнитного поля Н . Эти две величины связаны константой, которая зависит от конфигурации устройства, например для какой-либо катушки провода, от ее размера и формы. Эта связь выражается линейным уравнением Н = kI , хотя зачастую трудно найти точное значение k.

Индукция В связана с напряженностью поля уравнением В =μ H . В вакууме магнитная проводимость обозначается как μ 0и равна 4π·10 -7Н/А2.

Когда магнитное поле распространяется в среде, отличной от вакуума, магнитную проводимость μ представляют в виде произведения μ=μ 0μ r, где μ rотносительная магнитная проводимость среды. Последняя величина часто не является постоянной и зависит от тока.

После насыщения магнитного материала дальнейшее увеличение Н приводит лишь к незначительному увеличению В . Когда ток начинает уменьшаться, остаточная намагниченность магнитного материала изменяет зависимость В(Н), по которой индукция изменялась при увеличении тока, и в результате получается известная характеристика В(Н) с гистерезисным циклом.

PSpice использует для описания ферромагнитной катушки индуктивности — модели, основанной на теории Джилеса-Атертона (Jiles-Atherton) для магнитных доменов (ссылка в соответствующем разделе приложения E). Полное описание этой модели выходит за рамки данной работы, однако мы можем исследовать кривую В(Н) для различных условий и посмотреть, что происходит с токами и напряжениями в трансформаторах при насыщении.

Схема на рис. 13.3 содержит ферромагнитную катушку с обмоткой в 20 витков и сопротивлением R L =10 Ом. Обратите внимание, что команда для катушки индуктивности выглядит как

L1 1 0 20

где 20 представляет именно количество витков, а не индуктивность в 20 Гн. Это связано с присутствием во входном файле команды для модели, содержащей ключевое слово core . Если не использовать модель, последний параметр будет означать 20 Гн. Четыре генератора тока используются для создания низкочастотных синусоидальных колебаний с частотой 1 Гц. Первый генератор создает ток с максимальным значением 0,1 А и началом в момент t =0.

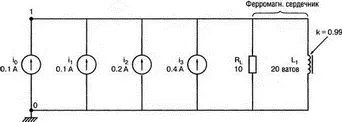
Рис. 13.3. Цепь для моделирования процесса в стальном магнитопроводе

Затем при t =1 с подключается следующий источник тока. Он также имеет максимальное значение 0,1 А. Затем подключаются третий и четвертый источники синусоидального тока в начале второй и третьей секунды соответственно. Амплитуда синусоидального тока увеличивается, чтобы показать влияние насыщения. Команда .MODEL использует ключевое слово core и позволяет учесть нелинейные магнитные параметры модели магнитопровода. Входной файл при этом:

This is the sample magnetic core problem

I0 0 1 sin(0 0.1A 1Hz 0)

I1 0 1 sin(0 0.1A 1Hz 1)

I2 0 1 sin (0 0.2A 1Hz 2)

I3 0 1 sin(0 0.4A 1Hz 3) RL 1 0 10

L1 1 0 20; - число витков =20, а не L = 20 Гн (используется модель)

K1 LI 0.99 KT; коэффициент связи

.model KT Core(MS=420E3 А=26 K=18 С=1.05 AREA=1.17 РАТН=8.49)

.options ITL5=0

.tran 0.1 4

.probe

.end

Выполните анализ в Probe и получите график В ( K 1) в функции времени. Он показывает нелинейную индукцию в магнитопроводе на временном интервале от 0 до 4 с. Обратите внимание, что на первых периодах нелинейность невелика по сравнению с более поздними периодами. Убедитесь, что значение первого максимума составляет В =1864 Э (эрстед), второй достигается при В =2965 Э, третий — при В =3989 Э, и заключительный — при B =4593 Э. Временная диаграмма приведена на рис. 13.4.

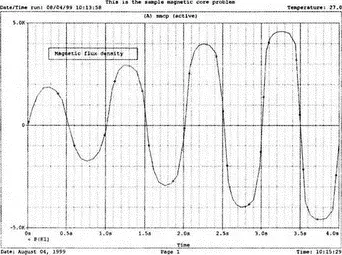
Рис. 13.4. Временная диаграмма магнитной индукции в магнитопроводе

Чтобы получить стандартную петлю гистерезиса В(Н ), замените величину, отложенную по оси Х на H ( R 1). Она представляет собой напряженность магнитного поля в магнитопроводе, пропорциональную току. По оси Y по-прежнему откладывается величина B ( R i ). На рис. 13.5 представлен этот график. Четыре петли гистерезиса соответствуют четырем уровням тока. Посмотрите, где на этой кривой появляются максимальные значения, показанные на предыдущем графике. Попробуйте изменить число витков, выполнить анализ снова и сравнить полученные результаты с предыдущими.

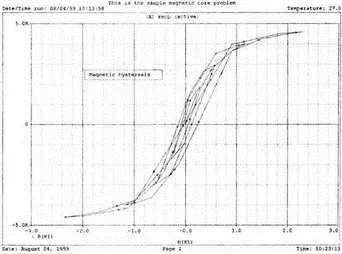
Рис. 13.5. Магнитный гистерезис в стальном магнитопроводе

Когда используется трансформатор с магнитопроводом из электротехнической стали, нелинейность характеристики магнитопровода влияет на форму тока вторичной обмотки. Чтобы показать это, рассмотрим схему (рис. 13.6), на которой представлен трансформатор, к первичной обмотке которого подключен источник тока. Параллельно источнику тока подключен резистор R 1, поскольку трансформатор нельзя подключать к идеальному источнику тока.

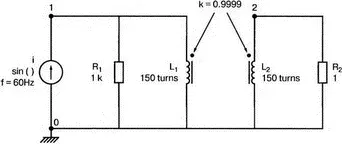
Рис. 13.6. Схема замещения трансформатора со стальным магнитопроводом

Первичная и вторичная обмотки содержат по 150 витков. Входной файл:

Iron-Core Transformer

i 0 1 sin (0 1А 60Hz)

R1 1 0 1k

L1 1 0 150 ; число витков первичной обмотки = 150

L2 2 0 150 ; число витков вторичной обмотки = 150

R2 2 0 1

K1 L1 L2 0.9999 KT

.model KT core ;- используется модель магнитопровода по умолчанию

.options ITL5 = 0

.tran 1ms 16.67ms

.end

Проведите анализ и получите в Probe графики i(R2) и i(L1). Убедитесь в том, что хотя первичный ток имеет форму синусоиды, вторичный ток сильно искажен. Эти графики приведены на рис. 13.7.

Рис. 13.7. Искажения формы тока вторичной обмотки трансформатора при сильном насыщении магнитопровода

Измените значение R 2и/или число витков каждой обмотки и сравните результаты с полученными ранее. Чтобы показать, что получается при меньшей степени насыщения, используйте следующий входной файл: