Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

FREQ I(R) I(RL) I(C) V(2) V(3)

1.592E+03 1.667E-03 1.667E-03 1.054E-03 1.000E+00 1.054E+00

FREQ V(4) VP(2) VP(4)

1.592E+03 1.000E+00 -2.884E-08 -3.688E+01

**** 07/31/99 12:20:00 *********** Evaluation PSpice (Nov 1998) **************

Constant-k Filter, Stop-Band Frequency of 6000 Hz

V 1 0 AC 1V

L 2 3 0.02H

L1 3 4 0.02H

С 3 0 0.1uF

R 1 2 0.01

LL 4 0 10.888mH

.AC LIN 1 6000Hz 6000Hz

.OPT nopage

.PRINT AC I(R) I(LL) I(C) V(2) V(3) V(4) VP(2) VP(4)

.END

**** AC ANALYSIS TEMPERATURE = 27.000 DEG С

FREQ I(R) I(LL) I(C) V(2) V(3)

6.000Е+03 2.436E-03 7.187E-04 3.155E-03 1.000E+00 8.369E-01

FREQ V(4) VP(2) VP(4)

6.000E+03 2.950E-01 1.396E-03 -1.800E+02

Рис. 12.24. Выходной файл для полосы пропускания и полосы подавления

Рис. 12.25. Вычисления в MathCAD для полосы подавления

Фильтр типа k может использоваться также в качестве полезной модели для линии передачи без потерь. На рис. 12.26 показан участок такой линии, включающий L =2 мГн и С=50 нФ. Допустим, что эта модель представляет участок реальной линии, длиной в 1 м. Значения L и С при этом являются удельной индуктивностью линии в мГн/м и удельной емкостью в нФ/м соответственно. Нетрудно определить частоту среза для этой линии равную f c =31,8 кГц. Проведем анализ для частоты f =10 кГц, лежащей в полосе пропускания.

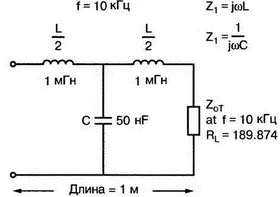
Рис. 12.26. Секция линии передачи без потерь

Чтобы согласовать линию с нагрузкой, необходимо найти Z 0T. Убедитесь, что Z 0T=189,874∠90° Ом. При использовании метода, описанного в предыдущем разделе, можно найти фазовый сдвиг β для участка линии. Убедитесь, что β=36,62°. Так как вычисления проводились для единичного участка линии, удельный фазовый сдвиг равен 36,620°/м. На рис. 12.27 показан результат вычислений для фильтра с постоянным k, проведенных в программе MathCAD. Входной файл для проверки полученных результатов на PSpice имеет вид:

Transmission Line as Lumped Elements

v 1 0 sin(0 1 10kHz)

L 1 2 1mH

L1 2 3 1mH

С 2 0 50nF

R 3 0 189.874

.tran 1us 100us

.probe

.end

Рис. 12.27. Результаты расчета фильтра с постоянным k в MathCAD

Проведите анализ и получите в Probe графики v(1) и v(3). Распечатайте полученные графики для дальнейшего изучения. Полученное выходное напряжение имеет большую амплитуду, чем входное. Переходя от максимумов напряжения к минимумам, достигаемым при отрицательных значениях, убедитесь, что минимум v(1) достигается в момент 75 мкс, в то время как соответствующий минимум v(3) — в момент 85 мкс. Запишите полученную минимальную величину v(3), которая равна -1,008 В, для будущего использования. Как можно интерпретировать временной интервал в 10 мкс между двумя колебаниями? Длина волны линии передачи λ=360°/β, что для нашего примера дает 360/36,62=9,83 м. Скорость распространения волны для частоты 10 кГц равна υ= f λ=98,3 км/с.

Между временем и расстоянием в линиях передачи существует, конечно, простая связь. В нашем примере мы заключаем, что линия длиной 98,3 км соответствует временной задержке в 1 с. То есть требуется время в 1 с, чтобы волна прошла вдоль этой линии. Длительность в 1 мкс соответствует расстоянию 0,0983 м. Временной интервал в 10 мкс — интервал времени между волнами v(1) и v(3) — эквивалентен 10×0,0983=0,983 м, что близко к длине рассматриваемого участка линии в 1 м.

Рассматривая более внимательно графики v(1) и v(3), мы обнаружим задержку напряжения v(3) в начале синусоидальной волны примерно на 10 мкс. Если вы дорисуете v(3) как синусоидальную волну, вы увидите, что она пересекает ось при 10 мкс. Программа Probe просто использует подходящую кривую, чтобы продлить график, маскируя таким образом эту деталь. Графики v(1) и v(3) показаны на рис. 12.28.

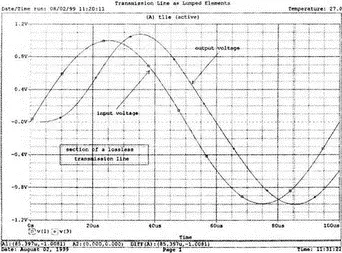
Рис. 12.28. Входное и выходное напряжения для линии без потерь

Удалите график напряжения и получите график i(R) для участка линии. Убедитесь, что минимум тока составляет -5,3 мА. Величина полного сопротивления нагрузки равна v | i =1,008/0,0053=190,2 Ом (напряжение было получено ранее). Так как ток и напряжение точно совпадают по фазе, 190,2 Ом представляет собой чисто активное сопротивление. Это соответствует значению Z 0T=189,874∠0° Ом.

Графики получены для временного интервала в 100 мкс, чтобы получить полный период синусоиды, но длина линии составляет только 1 м, что соответствует, как мы установили, 10 мкс.

Можно получить еще более убедительный график, удалив предыдущую кривую и получив временную зависимость v(3)/i(R). Как вы увидите, она имеет плоский участок. В режиме курсора выясните, что характеристическое сопротивление Z 0T = 189,9 Ом. Теперь получите на одном графике кривые i(R) и v(3)/190. Что при этом получилось и почему? Графики приведены на рис. 12.29.

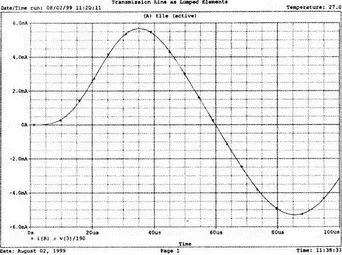
Рис. 12.29. Временные диаграммы тока и отношения выходного напряжения к характеристическому сопротивлению

Мы можем расширить анализ линий с постоянным коэффициентом k , моделирующих линии передачи без потерь, включив последовательно любое число участков. Используем, например, пять участков, как показано на рис. 12.30. Включим на вход линии источник с частотой 10 кГц и напряжением 1 В. Между участками включены резистивные датчики для измерения тока и напряжения.

Рис. 12.30. Линия передачи из пяти секций

Входной файл для такой схемы:

Transmission Line with 5 Sections

v 1 0 sin (0 1 10kHz)

R1 2 3 0.001

R2 4 5 0.001

R3 6 7 0.001

R4 8 9 0.001

RL 10 0 189.874

X1 1 0 2 LC

X2 3 0 4 LC

X3 5 0 a LC

X4 7 0 8 LC

X5 9 0 10 LC

.subckt LC 1 2 3

L 1 a 1mH

LI a 3 1mH

N a 2 50nF

.ends

.tran 1us 200us

.probe

.end

Проведите анализ и в Probe получите графики v(1), v(3), v(5), v(7), v(9) и v(10). Каждая волна перемещена относительно соседней на временной интервал, который необходим для прохождения одного участка цепи. Графики приведены на рис. 12.31.

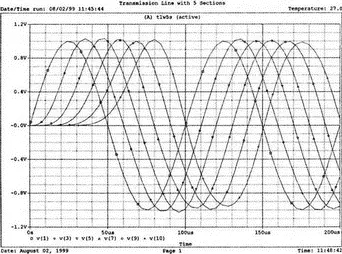
Рис. 12.31. Распространение волны по линии передачи