Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

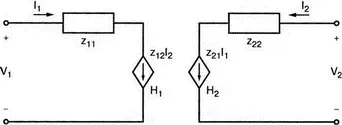
Рис. 12.13. Схема замещения для z-параметров на базе зависимого источника

Z-параметры для схемы переменного тока, подобной показанной на рис. 12.14, могут быть найдены с использованием PSpice. Мы найдем параметры холостого хода для этой схемы при частоте f =500 Гц. Удобно использовать источник тока в 1 А с нулевым фазовым углом на входе схемы. Входной файл:

Find z parameters for ас circuit

I1 0 1 an 1А

R1 1 3 20

R2 4 2 10

R3 3 0 50

L1 1 4 6366mH

C1 3 2 12.73uF

C2 3 0 3.183uF

.ac lin 1 500Hz 500Hz

.OPT nopage

.PRINT

.ac v(1) vp(1)

.END

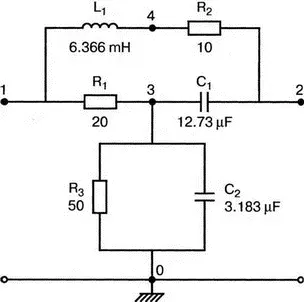
Рис. 12.14. Схема на переменном токе

Проведите анализ и убедитесь, что

V(1) = 5,199Е+01; VP(1) = -2,523Е+01; V(2) = -5,600Е+01;

VP(2) = -4,030Е+01,

откуда z 11=52∠-25,23° Ом и z 21=56∠-40,30° Ом.

Для нахождения других z -параметров подключим источник тока I 2в 1 А к выходу четырехполюсника. Входной файл не показан, так как он подобен предыдущему, но вы должны выполнить анализ и убедиться, что в результате получается

V(1) = 5,600Е+01; VP(1) = -4,030Е+01;

V(2) = 7,325Е+01; VP(2) = -3,463Е+01,

откуда z 12=56∠-40,30° Ом и z 22=73,25∠-34,63° Ом.

Поскольку используются только линейные элементы, схема симметрична и z 12= z 21.

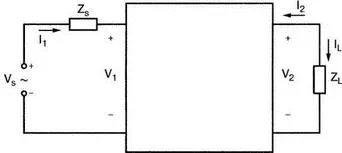
Рис. 12.15. Схема с источником и нагрузкой

Типичная схема имеет неидеальный источник с полным внутренним сопротивлением на входе и полное сопротивление нагрузки, подключенное к выходу (рис. 12.15). Можно показать, что

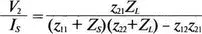
Некоторые из задач, приведенных в конце этой главы, связаны с использованием этого и подобных уравнений.

Еще одну группу параметров, которая широко используется при анализе силовых устройств, образуют параметры ABCD. Они основаны на уравнениях:

V 1= AV 2– BI 2;

I 1= CV 2– DI 2 .

Знак «минус» используется, чтобы согласовать эти уравнения с уравнениями для других параметров четырехполюсников, в которых ток I 2направлен к положительному полюсу четырехполюсника, а не нагрузки, как в последнем случае. Из основных уравнений следует, что

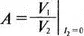
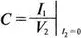
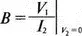
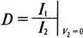
Таким образом, мы видим, что параметры А и С получены в режиме холостого хода на выходе четырехполюсника, а параметры В и D — при коротком замыкании выхода.

Линия передачи энергии часто представляется как последовательность Т -образных секций, подобных приведенной на рис. 12.16, где полное сопротивление последовательно включенной цепочки отображается индуктивностью и сопротивлением, а полное сопротивление параллельно подключенной цепочки — сопротивлением и емкостью. Чтобы найти параметры А и С, необходимо подать на вход напряжение 1 В с частотой 60 Гц при разомкнутом выходе. Входной файл:

Circuit to find A and N parameters

V1 1 0 ас 1V

L1 1 2а 0.24525Н

R1 2а 3 19.35

R3 3 0 4444

С1 3 0 3.06uF

.ас LIN 1 60Hz 60Hz

.ОРТ nopage

.PRINT ас v(3) vp(3) i(R1) ip(R1)

.END

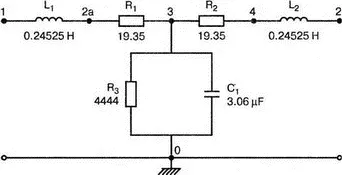
Рис. 12.16. Т-образная секция линии передачи

Элементы R 2и С 2не отражены в этом файле, так как цепь, в которую они включены, разомкнута. При этом напряжение V 3будет равно искомому напряжению V 2. Проведите анализ, который должен дать

V (3) = 1,113Е+00; VP (3) = -2,750Е+00;

I (R 1) = 1,308Е-03; IP(R 1) = 7,621Е+01.

Вычислив теперь отношение A = V 1 |V 2с помощью калькулятора, получим А =0,8985∠-2,75°. Параметр С определим из отношения I 1| V 2. Его значение равно 1,175∠-78,95° мС.

Параметры В и D найдем, подключив на вход источник напряжения в 1 В при короткозамкнутом выходе. Входной файл для такого опыта:

Circuit to find A and D parameters

V1 1 0 ас 1V

L1 1 2a 0.24525H

R1 2a 3 19.35

R2 4 3 19.35

L2 0 4 0.24525H

R3 3 0 4444

C1 3 0 3.06uF

.ac LIN 1 60Hz bOBz

.OPT nopage

.PRINT ac i(R2) ip(R2) i(R1) ip(R1)

.END

Выходной файл дает:

I ( R 2) = 5,577E-03; IP ( R 2) = 1.005E+01;

I ( R 1) = 5,012E-03; IP ( R 1) = -7,673E+01.

При коротком замыкании можно найти В и D с помощью калькулятора:

В = -V 1/ I 1= 179,3∠79,5° Ом;

С = - I 1/ I 2= 0,8987∠-2,77° Ом.

Как мы видим, А и D равны. Это будет происходить во всех схемах без источников питания, содержащих только линейные элементы. Из базовых уравнений можно непосредственно найти входные напряжение и ток, если известны аналогичные параметры на выходе передающей линии. Задачи, приведенные в конце главы, иллюстрируют этот метод.

Когда же известны условия на входе линии передачи, базовые уравнения полезно решить относительно V 2и I 2. При этом получим

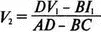
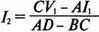
Можно показать, что

AD – ВС = 1.

Это дает возможность упростить выражения для выходных параметров

V 2= DV 1– BI 1;

I 2= CV 1- AI 1.

Когда в качестве независимых переменных выбраны входной ток и выходное напряжение, уравнения четырехполюсника записываются в виде:

V 1= h 11 I 1+ h 12 V 2;

I 2= h 21 I 1+ h 22 V 2.

Поскольку в уравнениях используются независимые переменные различного типа (ток и напряжение), соответствующие коэффициенты получили название гибридных параметров. Они уже знакомы нам под именем h -параметров и часто используются, чтобы характеризовать биполярные плоскостные транзисторы (BJT). Хотя такие параметры нетрудно найти для различных цепей постоянного и переменного тока, круг задач, не связанных с биполярными транзисторами, в которых применяются h -параметры очень ограничен. Из базовых уравнений можно получить: