Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

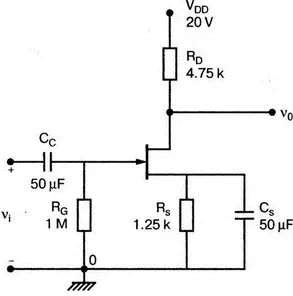
Рис. 11.22

11.5. Усилитель на базе транзистора JFET показан на рис. 11.23. Заданы значения r d =100 кОм и g m =2850 мкС. Используйте PSpice, чтобы найти коэффициент усиления по напряжению v 0| v s.

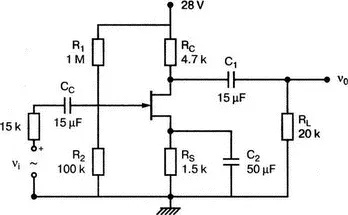
Рис. 11.23

11.6. Параметры усилителя на МОП-транзисторе, показанного на рис. 11.24: V T= 2,5 В, (β=0,6 А/В² и r d= 120 кОм. Используйте PSpice, чтобы найти коэффициент усиления по напряжению v 0| v s.

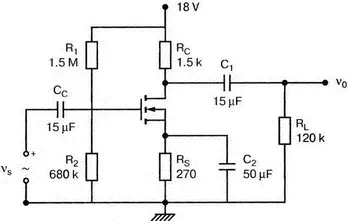
Рис. 11.24

11.7. Схема прерывателя показана на рис. 11.25. На вход схемы включен источник синусоидального напряжения v i с частотой 1 кГц и амплитудой, меньшей чем V РO . Управляющее напряжение v g имеет прямоугольную форму при частоте 2 кГц. Используйте анализ на PSpice/Probe, чтобы получить выходное напряжение v 0.

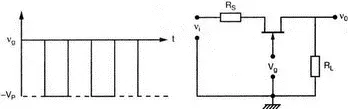
Рис. 11.25

В некоторых случаях схема может быть представлена в виде «черного ящика», имеющего два входных и два выходных полюса. Компоненты внутри могут быть либо неизвестны, либо не нужны для схемотехнического анализа, который необходимо выполнить. Такие схемы называются четырехполюсниками могут представлять собой набор резисторов, линию электропередачи, фильтр и т.п. Они могут даже содержать активные элементы.

Четырехполюсники имеют два входных полюса со стороны источника сигнала и два выходных полюса со стороны нагрузки. Для анализа этих цепей можно сначала узнать набор параметров, определяющих цепь, а затем использовать уравнения, составленные исходя из этих параметров. Этот метод анализа особенно полезен, когда изменяются источник сигнала и нагрузка, а сам четырехполюсник остается неизменным. Мы рассмотрим различные примеры, применяя для описания четырехполюсников параметры y, z, h и ABCD.

Базовые уравнения для определения параметров проводимости четырехполюсника:

I 1= y 11 V 1+ y 12 V 2;

I 2= y 21 V 1+ y 22 V 2.

Рис. 12.1. Четырехполюсник

На рис. 12.1 представлен четырехполюсник с условными направлениями токов и напряжений. Проводимости в сомножителях, содержащих V 1, можно вычислить при V 2=0 из выражений:

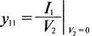
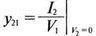
Таким образом, у 11определяется как отношение I 1к V 1при V 2=0, а у 12— как отношение I 2к V 1при V 2= 0. Аналогично

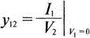
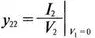
Эти y -параметры называются параметрами проводимости короткого замыкания четырехполюсника (short-circuit admittance parameters) и могут быть найдены с помощью PSpice. В качестве примера рассмотрим простую цепь, состоящую из резисторов.

На рис. 12.2 показана Т-образная схема, состоящая из трех резисторов. Чтобы найти у 11и y 21закоротим выход четырехполюсника (полюсы справа), обеспечив тем самым условие V 2 = 0. На вход четырехполюсника подадим напряжение V 1=1 В. Входной файл при этом имеет вид:

Input and Transfer Admittances

V1 1 0 1V

R1 1 2 12

R2 0 2 3

R3 2 0 6

.DC V1 1V 1V 1V

.ОРТ nopage

.PRINT DC I(R1) I(R2); для y11 and y21

.END

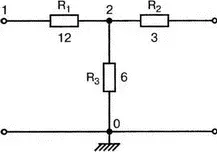
Рис. 12.2. Т -образная схема замещения

Обратите внимание, что в команде, описывающей резистор R 2, узлы записаны в следующем порядке: 0, 2. Тем самым задается направление для тока I 2, показанное на рис. 12.3. Проведите анализ на PSpice, чтобы найти I 1и I 2. В результате вы получите

I( R 1) = 71,43 мА и I( R 2) = -47,62 мА.

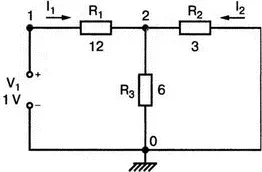
Рис. 12.3. Т -образная схема с короткозамкнутым выходом

Поскольку напряжение V 1выбрано равным 1 В, значение I 1численно равно проводимости у 11, а значение I 2численно равно проводимости у 21. Следовательно,

y 11= 71,43 мс и у 21= -47,62 мс.

Остальные y-параметры могут быть найдены при подаче со стороны выхода напряжения V 2=1 В и при V 1=0. Последнее условие выполняется при коротком замыкании на входе. Входной файл:

Output and Transfer Admittances

V2 2 0 1V

R1 0 1 12

R2 2 1 3

R3 1 0 6

.DC V2 1V 1V 1V

.OPT nopage

.PRINT DC I(R1) I(R2); для y12 and y22 .END

Поскольку напряжение V 2выбрано равным 1 В, значение I 1, численно равно проводимости у 12, а значение I 2численно равно проводимости у 22. Проведите анализ и убедитесь, что

у 12= -47,62 мс и у 22= 142,9 мс.

Обратите внимание, что у 12= у 21и, следовательно, четырехполюсник является симметричным.

Отрицательные знаки для проводимостей у 12= у 21не несут в себе какого-либо физического смысла, поскольку y-параметры не отражают свойств физических элементов. Однако легко показать, что П -образная схема на рис. 12.4 эквивалентна четырёхполюснику, описываемому y-параметрами, и поэтому она эквивалентна исходной схеме, заключенной в «черном ящике», какой бы она ни была. В нашем примере

y а= y 21+ y 21= 23,81 мс;

y b= y 22+ y 12= 95,28 мс;

y с= -y 12= 47,62 мс.

При этом реальные проводимости в схеме на рис. 12.4 положительны.

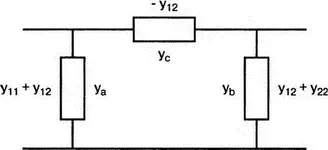
Рис. 12.4. Схема замещения для y -параметров

Если преобразовать y -параметры в z -параметры (для нашего случая в r -параметры), вычислив обратные величины, то получим z a =42 Ом, z b= 10,5 Ом и z c =21 Ом.

Другая схема замещения, содержащая y-параметры, показана на рис. 12.5. В ней используются два зависимых источника тока, управляемых напряжением (ИТУН/VDCS), и она следует непосредственно из исходных уравнений для y-параметров. Вспомним, что команда, предназначенная для введения во входной файл таких источников, должна начинаться с символа G .