Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Transmission-Line Representation

V 1 0 AC 1V

R1 1 2 0,01

R2 3 4 0,01

R3 5 6 0.01

R4 1 8 0.01

R5 9 10 0.01

R6 11 12 0.01

R7 13 14 0.01

R8 15 16 0.01

R9 17 18 0.01

R10 19 20 0.01

RL 21 22 724.567

CL 22 С 1.154uF

X1 2 0 3 TLINE

X2 4 0 5 TLINE

X3 6 0 7 TLINE

X4 8 0 9 TLINE

X5 10 0 11 TLINE

X6 12 0 13 TLINE

X7 14 0 15 TLINE

X8 16 0 17 TLINE

X9 18 0 19 TLINE

X10 20 0 21 TLINE

.subckt TLINE 1 2 6

R 1 3 101.5

R1 4 5 101.5

L 3 4 39.3mH

L1 5 6 39.3mH

Rs 4 2 0.172Meg

С 4 2 0.159uF

.ends

.OPT nopage

.AC LIN 1 795.8Hz 795.8Hz

.PRINT AC I (R1) I(R2) I(R3) I(R4) I(R5) I(R6) I(R7) I(R8) I(R9) I(R10) I(RL)

.PRINT AC V(2) V(4) V(6) V(8) V(10) V(12) V(14) V(16) V(18)V(20) V(21)

.PRINT AC VP(2) VP(4) VP(6) VP(8) VP(10) VP(12) V(14) VP(16) VP(18) VP(20) VP(21)

.END

**** AC ANALYSIS TEMPERATURE = 27.000 DEG С

FREQ I(R1) I(R2) I(R3) I(R4) I(R4)

7.956E+02 1.392E-03 1.202E-03 1.0301-03 8.953E-04 7.693E-04

FREQ I(R6) I(R7) I(R8) I(R9) I(R10)

7.958E+02 6.608E-04 5.709E-04 4.967Е-04 4.300E-04 3.678E-04

FREQ I(RL)

7.958E+02 3.104E-04

FREQ V(2) V(4) V(6) V(8) V(10)

7.958Е+02 1.000E+00 8.613E-01 7.412E-01 6.390E-01 5.528E-01

FREQ V(12) V(14) V(16) V(18) V(20)

7.958E+02 4.784E-01 4.117Е-01 3.518E-01 3.015E-01 2.626E-01

FREQ V(21)

7.958E+02 7.312E-01

FREQ VP(2) VP(4) VP(6) VP(8) VP(10)

7.958E+02 -1.676E-04 -3.330E+01 -6.671E+01 -1.002E+02 -1.337E+02

FREQ VP(12) VP(14) VP(16) VP(18) VP(20)

7.953E+02 -1.669Е+02 1.601E+02 1.268E+02 9.283E+01 5.873E+01

FREQ VP(21)

7.958E+02 2.568E+01

Рис. 12.21. Выходной файл с результатами анализа схемы на рис. 12.20

Фильтр с постоянным коэффициентом k [7] Фильтрами с постоянным коэффициентом k , или фильтрами типа k , называются устройства, у которых в продольную и поперечные ветви включены взаимно-обратные двухполюсники. При этом произведение сопротивлений Z 1 · Z 2 = k ² является постоянной величиной на любых частотах, следовательно, постоянен и коэффициент k , имеющий размерность сопротивления. ( Прим. переводчика. ) (фильтры типа k ) в идеале должен быть составлен из чисто реактивных сопротивлений. В самой простой форме он мог бы представлять собой низко- или высокочастотный фильтр. Т -образная секция низкочастотного фильтра показана на рис. 12.22. Параметры элементов, выбранные для этого примера: L =0,04 Гн и С =0,1 мкФ. Такой фильтр обычно нагружен на полное выходное сопротивление, равное характеристическому:

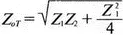
где Z 1= jωL и Z 2= 1/( jωС ).

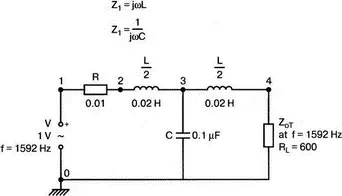
Рис. 12.22. Низкочастотный фильтр с постоянным k

При частоте f =1592 Гц сопротивление Z 0T = 600 Ом является чисто активным. На рис. 12.22 источник напряжения с внутренним сопротивлением R =0,01 Ом подключен на вход, значение сопротивления нагрузки R L= 600 Ом. В результате анализа на PSpice найдем входные и выходные токи и напряжения. Входной файл:

Constant-k Filter, Pass-Band Frequency of 1592Hz

V 1 0 AC 1V

L 2 3 0.02H

L1 3 4 0.02H

N 3 0 0.1uF

R 1 2 0.01

RL 4 0 600

.AC LIN 1 1592Hz 1592Hz

.OPT nopage

.PRINT AC I(R) V(2) V(3) V(4) VP(2) VP(4)

.END

Проведите анализ и получите распечатку выходного файла. Интерпретируя результаты, вспомним, что при частоте f =1592 Гц, характеристическое сопротивление является чисто активным. Частота находится в полосе пропускания, где сигнал проходит вообще без ослабления (α=0). Это означает, что входной и выходной токи попросту равны. Убедитесь, что входной ток I(R) и выходной I(RL) составляют по 1,667 мА. Сдвиг фазы для фильтра задается выражением

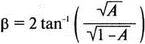
где

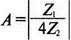
Рассчитанное по этой формуле значение для сдвига фазы равно 36,88°, что совпадает с результатом, полученным на PSpice (выходной файл также дает VP(4) = 36,88°).

Фильтр нижних частот имеет частоту среза, равную

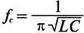
что для выбранных параметров элементов дает f c =5033 Гц. Для сравнения на рис. 12.23 приведены результаты вычисления полосы пропускания для фильтра с постоянным k, полученные в программе MathCAD.

Рис. 12.23. Расчет фильтра с постоянным k в программе MathCAD

Продолжим рассмотрение примера для фильтра низких частот. При частоте f =6 кГц, находящейся в полосе подавления, сигнал должен быть передан с некоторым ослаблением. Чтобы согласовать нагрузку фильтра, вычислим значение Z 0Tпри частоте 6 кГц. Оно оказывается равным Z 0T= j 410,47 Ом, что соответствует индуктивности нагрузки L =10,888 мГн.

Рассмотрим теперь реакцию фильтра при f =6 кГц. Изменим входной файл:

Constant-k Filter, Stop-Band; Frequency 6 kHz

V 1 0 AC 1V

L 2 3 0.02H

L1 3 4 0.02H

N 3 0 0.1uF

R 1 2 0.01

LL 4 0 10.88 8mH

.AC LIN 1 6000HZ 6000Hz

.PRINT AC I(R) I(LL) I(C) V(2) V(3) V(4) VP(2) VP(4)

.OPT nopage

.END

Проведите анализ и получите распечатку выходного файла. Убедитесь, что входной ток I(R)=2,436 мА, а выходной I(RL)=0,7187 мА. Фазовый сдвиг β соответствует в выходном файле VP(4)=–180°. Коэффициент распространения равен

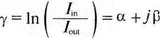
Из наших результатов γ=ln(3,3895∠180°). Значение α находится как десятичный логарифм от модуля γ и равно α=1,22 Нп (непер). Формула для определения α:

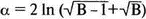
где

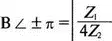
Полученное расчетное значение α=1,22 Нп соответствует результату, полученному в PSpice. Непер — основная единица ослабления, соответствующая отношению входного тока к выходному в 2,71728. Проведя соответствующие преобразования, можно получить 1 Нп = 8,686 дБ. На рис. 12.24 показан выходной файл для полосы пропускания и полосы подавления. MathCAD вычисления для полосы подавления даны на рис. 12.25.

**** 07/31/99 12:13:52 *********** Evaluation PSpice (Mov 1998) **************

Constant-k Filter, Pass-Band Frequency of 1592 Hz

V 1 0 AC 1V

L 2 3 0.02H

L1 3 4 0.02H

С 3 0 0.1uF

R 1 2 0.01

RL 4 0 600

.AC LIN 1 1592Kz 1592Hz

.OPT nopage

.PRINT AC I(R) I(RL) I(C) V(2) V(3) V(4) VP(2) VP(4)

.END

**** AC ANALYSIS TEMPERATURE = 27.000 DEG С