Дж. Кеоун - OrCAD PSpice. Анализ электрических цепей

Чтобы провести измерения оставьте, на экране только графики v(1) и v(10). Определите, в какой точке каждая кривая пересекает ось X , переходя к отрицательным значениям. Убедитесь, что для v(1) это происходит при t =50 мкс, а для v(10) при t =100 мкс. Это означает, что общая задержка линии составляет 50 мкс. Хотя графики построены во временном интервале для 200 мкс, длина линии соответствует только 50 мкс, синусоидальные кривые дают ясное представление о прохождении волны по линии передачи.

Когда линия передачи согласована с нагрузкой, полное входное сопротивление должно быть равно характеристическому сопротивлению линии, из скольких бы участков она ни состояла. Анализ для переменных составляющих позволит легко получить результаты для амплитуд и фаз напряжений и токов. Продолжим исследования предыдущего примера, включив во входной файл анализ переменных составляющих:

Transmission Line with 5 Sections Modified

v 1 0 sin(0 1 10kHz)

R1 2 3 0.001

R2 4 5 0.001

R3 6 7 0.001

R4 8 9 0.001

RL 10 0 189.874

X1 1 0 2 LC

Х2 3 0 4 LC

Х3 5 0 a LC

Х4 7 0 8 LC

Х5 9 0 10 LC

.subckt LC 1 2 3

L 1 a 1mH

L1 а 3 1mH

N a 2 50nF

.ends

.OPT nopage

.ac lin 1 10kHz 10kHz

.print ac v(10) i(RL) vp(10) ip(RL)

.print ac v(9) i(R4) vp(9) ip(R4)

.print ac v(7) i(R3) vp(7) ip(R3)

.print ac v(5) i(R2) vp(5) ip(R2)

.print ac v(3) i(R1) vp(3) ip(R1)

.end

Проведите анализ и рассмотрите выходной файл. На выходе линии V(10)=1 В и I(RL)=5,267 мА. Угол сдвига между этими двумя синусоидами составляет 176,9. Это дает для полного сопротивления Z=189,86∠0°, что соответствует характеристическому сопротивлению. Полное входное сопротивление для следующего разделе найдем из V(9)=1 В и I(R4)=5,267 мА, VP(9)=–146,5° и IP(R4)=-146,5°. Величины напряжения и тока не отличаются от предыдущих, они по-прежнему находятся в фазе, полное сопротивление снова равно характеристическому сопротивлению. Обратите внимание, что на смежных участках линии значения напряжений и токов остаются прежними, но сдвигаются на угол 36,6°. Выходной файл приведен на рис. 12.32.

**** 08/02/99 11:59:12 *********** Evaluation PSpice (Nov 1998) **************

Transmission Line with 5 Sections Modified

v 1 0 ас 1

R1 2 3 0.001

R2 4 5 0.001

R3 6 7 0.001

R4 8 9 0.001

RL 10 0 189.874

X1 1 0 2 LC

X2 3 0 4 LC

X3 5 0 6 LC

X4 7 0 8 LC

X5 9 0 10 LC

.subckt LC 1 2 3

L 1 a 1mH

L1 a 3 1mH

С a 2 50nF

.ends

.opt nopage

.ac lin 1 10kHz 10kHz

.print ac v(1) i(RL) vp(10) ip(RL)

.print ac v(9) i(R4) vp(9) ip(R4)

.print ac v(7) i(R3) vp(7) ip(R3)

.print ac v(5) i(R2) vp(5) ip(R2)

.print ac v(3) i(R1) vp(3) ip(R1)

.end

**** AC ANALYSIS TEMPERATURE = 27.000 DEG С

FREQ V(10) I(RL) VP(10) IP(RL)

1.000E+04 1.000E+00 5.267E-03 1.769E+02 1.769E+02

FREQ V(9) I(R4) VP(9) IP(R4)

1.000E+04 1.000E+00 5.267E-03 -1.465E+02 -1.465E+02

FREQ V(7) I(R3) VP(7) IP(R3)

1.000E+04 1.000E+00 5.267E-03 -1.099E+02 -1.099E+02

FREQ V(5) I(R2) VP(5) IP(R2)

1.000E+04 1.000E+00 5.267E-03 -7.324E+01 -7.324E+01

FREQ V(3) I(R1) VP(3) IP(R1)

1.000E+04 1.000E+00 5.267E-03 -3.662E+01 -3.662E+01

Рис. 12.32. Выходной файл с результатами анализа схемы на рис. 12.30

Результаты ясно указывают на плоскую линию (без отражения), в которой не возникают стоячие волны. Это типично для линий, на выходе которых включено сопротивление, равное их характеристическому сопротивлению.

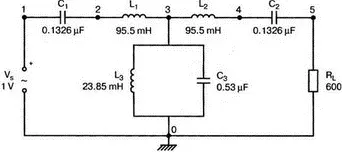
Рис. 12.33. Полосовой фильтр

Более сложный пассивный фильтр показан на рис. 12.33. И последовательные, и параллельные элементы содержат емкость и индуктивность. Формулы для элементов приведены в книге Ware and Reed, Communication Circuits на с. 166 и показаны здесь для справки:

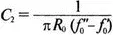
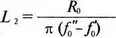
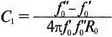
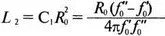
Полоса пропускания лежит между частотами f' 0и f'' 0. Фильтр должен быть рассчитан на 600 Ом, чтобы полоса пропускания лежала в диапазоне от 1 до 2 кГц. Входной файл для этого случая:

Band-pass Filter Using Passive Elements

Vs 1 0 ас 1V

C1 1 2 0.1326uF

C2 4 5 0.1326uF

C3 3 0 0.536uF

L1 2 3 95.5mH

L2 3 4 95.5mH

L3 3 0 23.85mH

RL 5 0 600

.ac DEC 50 100Hz 10kHz

.PROBE

.END

Получите в Probe частотную характеристику, приведенную на рис. 12.34. Поскольку ослабление за границами области пропускания очень велико, измените границы по оси Y, установив их от -50 до 10. Отметим, что вблизи центра области пропускания почти не наблюдается снижения кривой и вследствие резонансного характера цепи характеристика резко снижается сразу за границами области пропускания. В качестве упражнения найдите усиление для каждого из максимумов. Убедитесь, что для первого максимума оно составляет 3,62 дБ, а для второго — 3,72 дБ. Найдите также ослабление при f =2,4 кГц.

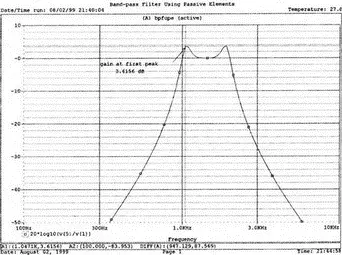
Рис. 12.34. График Боде для полосового фильтра

Реальные элементы, в особенности катушки индуктивности, обладают некоторым активным сопротивлением. В задачах, приведенных в конце главы, это обстоятельство учитывается.

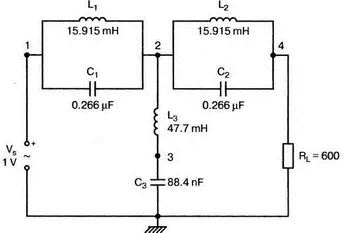
Рис. 12.35. Заградительный фильтр

Если в Т -образной секции, исследованной в предыдущем разделе, использовать параллельно соединенные катушку индуктивности и конденсатор (параллельный колебательный контур) в последовательных ветвях и последовательный колебательный контур в параллельной ветви (рис. 12.35), то мы получим заградительный фильтр. При расчете снова используются формулы из Ware and Reed, Communication Circuit для полосы заграждения от 2 до 3 кГц. Уравнения имеют вид:

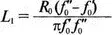
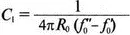
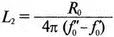
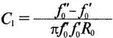
Полоса подавления лежит между частотами f' 0и f'' 0. Параметры элементов приведены на рис. 12.35, входной файл: