Компьютерра - Журнал «Компьютерра» №35 от 28 сентября 2005 года

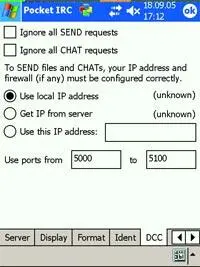
Судя по тому, как динамично обновляется и обрастает новыми опциями wmIRC, можно предположить, что через месяц-другой этот клиент дорастет до DCC и станет недосягаем для конкурентов, пока же приходится держать на КПК обоих клиентов.

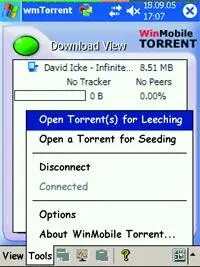
Вне конкуренции уже сегодня находится программа для работы с торрентами WinMobile Torrent (рис. 3). Очаровательнейший VGA-интерфейс и как по маслу интеграция в операционную систему превращают работу с торрентами в сплошное удовольствие: запускаем браузер, отправляемся на поисковый торрент-портал (адреса смотрите на beritut в майской колонке «Креатифф и Bit Torrent»), находим нужную программу (фильм, книгу, фотографию), кликаем на линк с расширением torrent — информационный файл автоматически загружается на КПК и сразу же автоматически передается WinMobile Torrent, который питбульной хваткой вытягивает из Сети нужный артефакт, пока вы занимаетесь другими делами (разумеется, в фоновом многозадачном режиме — ау, Пальма — Банана!).

В свое время я долго носился с RSS-каналами и даже рекомендовал несколько программ в «Тактильной Саге». Увы, программы эти не выдержали испытания временем, и пришлось довольствоваться проприетарным Mobilizer’ом. Как идея Mobilizer был прекрасен, однако разработчики (наша Quarta) похерили свое детище по полной программе, и оно не преминуло зачахнуть. Глядя на непристойно грибной рост русских RSS-каналов, перечисленных в лучшем профильном каталоге KANBAN, я возобновил поиск клиента, и мои потуги почти мгновенно увенчались безоговорочным успехом: программа NewsBreak от культового создателя ListPro Ilium Software практически идеальна (рис. 4).

Бог с ним, с идеальным VGA и полной поддержкой изображений, главное — это море настроек по планированию и автоматизации загрузки каждого RSS-канала в отдельности, чего так не хватало у конкурентов. Добавьте сюда плагин для экрана Today и вы получите идеальный RSS-клиент под Windows Mobile.

Заключительный аккорд в сегодняшней теме принадлежит программе WinMobile Download Accelerator — классическому менеджеру загрузок (рис. 5).

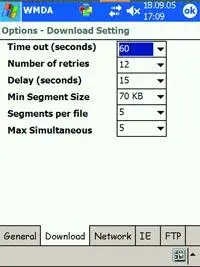
Программа перехватывает у браузера любые линки с заданными расширениями (exe, zip, rar и т. п.), разделяет файл на настраиваемое число сегментов и далее в многопоточном режиме осуществляет ускоренную загрузку, разумеется, с поддержкой прерванных соединений и в фоновом режиме — всего того, без чего мы давно уже не мыслим существование на стационарном дедушке «писюке».

Линки, помянутые в «Голубятне», вы найдете на домашней странице internettrading.net/guru.

8 августа 1900 года на 2-м Международном конгрессе математиков в Париже один из величайших математиков современности Давид Гильберт сформулировал двадцать три задачи, которые во многом предопределили развитие математики XX столетия. В 2000 году специалисты из Clay Mathematics Institute решили, что грешно входить в новое тысячелетие, не наметив новую программу развития, -тем более что от двадцати трех проблем Гильберта остались лишь две[Еще две считаются слишком расплывчатыми или нематематическими, еще одна была решена частично, а по поводу еще одной — знаменитой континуум-гипотезы — консенсус пока не достигнут ( подробнее об этом)].

В результате появился знаменитый список из семи задач, за полное решение любой из которых обещан миллион долларов из специально учрежденного фонда. Чтобы получить деньги, нужно опубликовать решение и подождать два года; если в течение двух лет никто его не опровергнет (будьте уверены — попытаются), вы получите миллион вожделенных зеленых бумажек.

Я попытаюсь изложить суть одной из этих задач, а также постараюсь (в меру своих скромных сил) объяснить ее сложность и важность. Настойчиво рекомендую зайти на официальный сайт конкурса www.claymath.org/millennium; опубликованные там описания проблем полны и интересны, и именно они стали главным источником при написании статьи.

Однажды один из моих научных руководителей, выдающийся петербургский алгебраист Николай Александрович Вавилов, начал занятие своего спецкурса с формулы

1 + 2 + 3 + 4 + 5 + … = —1/12.

Нет, занятие не было посвящено гипотезе Римана, и узнал я о ней вовсе не от Николая Александровича. Но формула, тем не менее, имеет к гипотезе самое прямое отношение. И что удивительно — это кажущееся абсурдным равенство действительно верно. Точнее сказать, не совсем оно, но дьявол деталей тоже вскоре будет удовлетворен.

В 1859 году Бернард Риман (Bernhard Riemann) опубликовал статью (или, как тогда выражались, мемуар), которой была суждена очень долгая жизнь. В ней он изложил совершенно новый метод асимптотической оценки распределения простых чисел. В основе метода лежала функция, связь которой с простыми числами обнаружил еще Леонард Эйлер, но которая все же получила имя математика, продолжившего ее на всю комплексную плоскость: так называемая дзета-функция Римана. Определяется она очень просто:

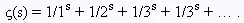
Любой студент, прослушавший курс математического анализа, тут же скажет, что этот ряд сходится для всякого вещественного s > 1. Более того, он сходится и для комплексных чисел, вещественная часть которых больше единицы. Еще более того, функция ς(s) — аналитическая в этой полуплоскости.

Рассматривать формулу для отрицательных s кажется дурной шуткой: ну какой смысл складывать, например, все положительные целые числа или, тем более, их квадраты или кубы? Однако комплексный анализ — упрямая наука, и свойства дзета-функции таковы, что ее можно продолжить на всю плоскость. Это и было одной из идей Римана, изложенных в мемуаре 1859 года. У полученной функции только одна особая точка (полюс): s = 1, а, например, в отрицательных вещественных точках функция вполне определена. Именно значение аналитически продолженной дзета-функции в точке —1 и выражает формула, с которой я начал этот раздел.

(Специально для патриотов и неравнодушных к истории науки людей отмечу в скобках, что, хотя мемуар Бернарда Римана внес в теорию чисел много свежих идей, он не был первым исследованием, в котором распределение простых чисел изучалось аналитическими методами. Впервые это сделал наш соотечественник Пафнутий Львович Чебышёв, 24 мая 1848 года прочитавший в петербургской Академии наук доклад, в котором изложил ставшие классическими асимптотические оценки количества простых чисел.)