Валентин Арьков - Эконометрические оценки. Учебное пособие

© Валентин Юльевич Арьков, 2021

ISBN 978-5-0055-3064-6

Создано в интеллектуальной издательской системе Ridero

Данное учебное пособие основано на серии лекций, прочитанных автором в дистанционном режиме. Видеозаписи лекций доступны на канале автора на Youtube. Ссылки на видеоролики имеются в конце данного пособия.

Наш предмет называется ЭКОНОМЕТРИКА. Существует эконометрика достаточно давно. На Западе – уже десятки лет преподаётся как самостоятельная дисциплина. В России эконометрика «появилась» лет двадцать-тридцать тому назад – как следование западной моде.

Смысл в том, что 30 лет назад это была какая-то абстрактная теория, непонятное ответвление статистики. На сегодняшний день это работающие программы и технологии. Когда мы слышим про загадочные «большие данные» – Big Data, про анализ больших данных или про науку о данных – Data Science – за этим скрывается то, что как раз и изучается в курсе «Эконометрика».

Мы с вами будем разбирать очень практические вещи. Соответственно, и в лекциях, и на лабораторных работах у вас будет именно практическая сторона материала.

Весь предмет эконометрики сводится к задаче регрессии.

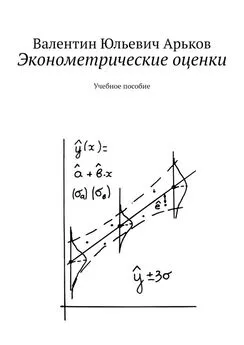
У нас имеется некоторое количество данных, которые условно можно назвать «иксы» и «игреки». Их можно изобразить в виде точек. Это могут быть люди, станки, квартиры, предприятия, страны. Имеем массив числовых значений и точек на графике. По этим точкам нужно В СРЕДНЕМ провести какую-нибудь линию, см. рис.

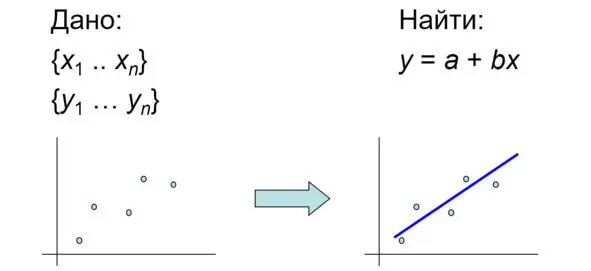
Рис. Регрессия – линия в среднем по точкам

Это может быть прямая, или кривая, или даже ломаная.

Если нанести точки на плоском графике и нужно построить прямую линию, то достаточно приложить линейку и провести линию. Главное, что это должно в среднем. Это значит, что линия может вообще не пройти ни по одной точке. Она пройдет там, где густо. Там, где много точек.

Такая технология называется РЕГРЕССИЯ.

На занятиях по бизнес-аналитике и статистике мы с разных сторон рассмотрим историю и разберём данный раздел.

Буквально слово «регрессия» означает «движение назад». В большинстве случаев это действительно возвращение или противоположность прогрессу и т. п. – кроме нашей ситуации. В эконометрике и в статистике слово «регрессия» означает «провести по точкам подходящую линию». По сути это попытка получить очень упрощенную закономерность из большого количества данных.

Вспомним школьный курс математики и геометрии. Прямую линию можно провести только через две точки. Это математика.

В статистике и в эконометрике мы говорим по-другому. Чтобы провести прямую линию, нужно 100 точек, а лучше 1000, а ещё лучше 1000000. Наша линия пройдет по ним в среднем. Эта идея в самых разных видах и будет рассматриваться.

Самый простой инструмент, с которым мы будем работать, – это табличный редактор, или электронная таблица. Это может быть Microsoft Excel или любой другой подобный программный продукт. Существует множество программ, которые совместимы с Excel на уровне формата файла. Есть бесплатный продукт – Libre Office Calc. Это могут быть облачные средства, например, Таблицы Гугл – Google Sheets.

На экране мы видим столбец иксов и столбец игреков. На графике нанесены эти точки. Можно себе представить, что это люди разного роста и разного веса. Каждого человека измерили и взвесили.

Теперь мы хотим получить среднюю, общую закономерность. Если мы выберем людей с очень красивой фигурой и с очень хорошим здоровьем, тогда можно будет говорить про «формулу идеального веса», см. рис.

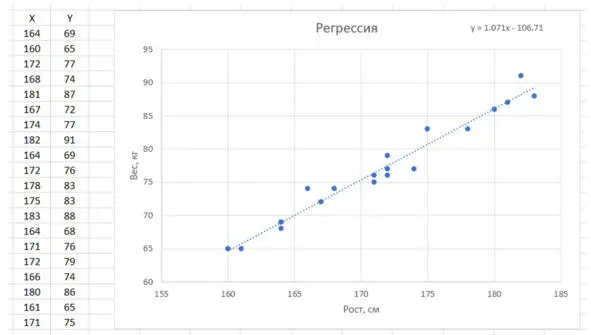
Рис. Линия регрессии в Excel

Предмет «Эконометрика» имеет некоторое отношение к экономике, к услугам, к товарам. Можно использовать знание таких закономерностей и для мониторинга здоровья сотрудников компании. Многие предприятия отправляют работников на регулярный медосмотр. При этом можно выяснить, у кого излишний вес, у кого нормальный, у кого недостаточный. Это может влиять на здоровье сотрудников, а значит, и на работу предприятия. Лучше потратить средства на поддержание здоровья, чем на лечение или срочную замену в самый неподходящий момент. Конечно, это будет важно для тех, кого интересует долгосрочное существование компании.

Другой пример. Пускай в качестве иксов у нас будет площадь квартиры, а по игреку – стоимость квартиры. Тогда мы можем рассматривать такую финансовую закономерность: сколько стоит квадратный метр в среднем и сколько может стоить конкретная квартира?

Есть множество таких ситуаций, где можно найти и использовать подобную зависимость. Хорошо, если есть всего один икс и один игрек. Это можно представить на плоскости. А если будет 20 иксов и 30 игреков? А если 120 иксов? Это на плоскости сложно изобразить – и от руки, и на компьютере.

Разберем простую демонстрацию того, как выглядит регрессионный анализ.

Запускаем Excel.

Перед нами столбец иксов и столбец игреков.

Мы выделяем эти столбцы, выбираем Вставка – График — … Находим в серединке кнопочку « Точечная диаграмма». По-английски это называется Scatter Plot, по-русски – диаграмма разброса. У нас появилась картинка, см. рис.

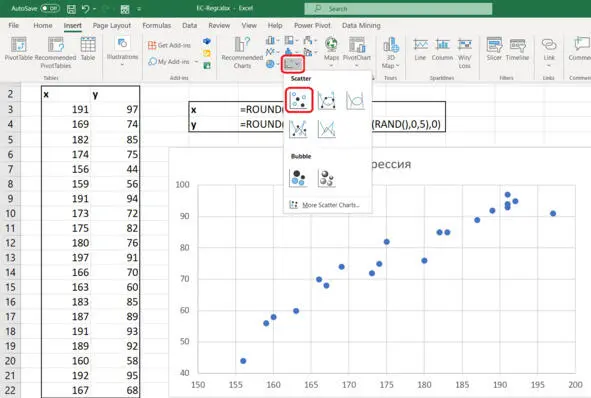
Рис. Исходные данные и диаграмма разброса

Наши игреки начинаются не от нуля, поэтому мы настроим ось координат. Задаём минимальное значение 40, максимальное 110.

Нажимаем плюсик справа от диаграммы и добавляем «линию тренда». Вообще-то слово «тренд» означает «тенденция изменений, общее направление развития». Но в данном случае это просто общая закономерность. Мы говорим, что нас интересует прямая линия. На графике появляется прямая.

Мы хотели бы вывести уравнение этой линии на экран. Нажимаем More Options – Дополнительные параметры. Затем Display equation on chart – Вывести уравнение на график. Получаем уравнение нашей линии, см. рис.

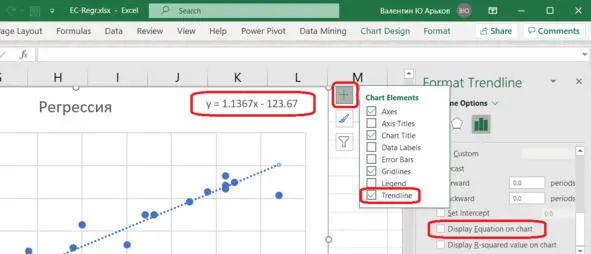
Рис. Уравнение и линия регрессии

Это самый простой вариант: как мы можем в среднем по точкам провести линию. Естественно, здесь есть масса нюансов, масса тонкостей. Это самая общая идея того, что нам предстоит освоить.