Владимир Яшин - Информатика: аппаратные средства персонального компьютера

Числа записываются с использованием особых знаковых систем, которые называются системами счисления, в них числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на два вида: позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, в непозиционных – не зависит. Самой распространенной из непозиционных систем является римская. В качестве цифр в римской системе используются следующие символы: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Значение цифры в этой системе не зависит от ее положения в числе. Величина числа в римской системе определяется как сумма и разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.

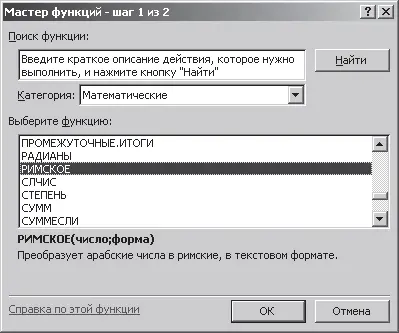
Рис. 2.2. Диалоговое окно «Мастер функций – шаг 1 из 2»

Например, число 1997 (десятичная позиционная система счисления) в римской системе счисления будет выглядеть следующим образом: MCMXCVII = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1. Для автоматизации процесса перевода данного числа из десятичной в римскую систему счисления воспользуемся табличным процессором MS Excel.

Для запуска программы MS Excel выполним команду: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel]. В любую из ячеек открывшегося окна Excel введем функцию «Римское», которая и осуществит необходимый перевод. Выполним следующие действия. Выделим, например, ячейку А1 с помощью курсора и выполним следующую команду: [Вставка – Функция]. В открывшемся диалоговом окне «Мастер функций – шаг 1 из 2» (рис. 2.2), установим «Категория: Математические» и выберем функцию «Римское». После нажатия кнопки OKпоявится диалоговое окно «Аргументы функции», показанное на рис. 2.3. Введем число 1997 в соответствующее поле окна и нажмем кнопку OK.

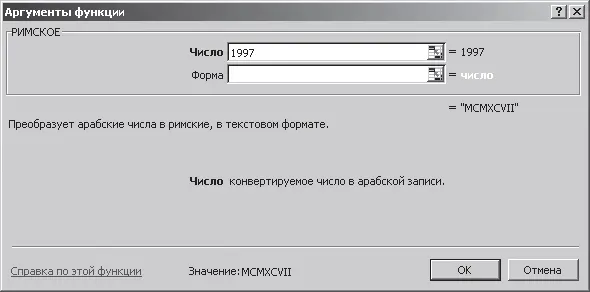
Рис. 2.3. Диалоговое окно «Аргументы функции»

В результате этих действий получаем в ячейке А1 искомое значение числа 1997 в римской системе счисления (рис. 2.4).

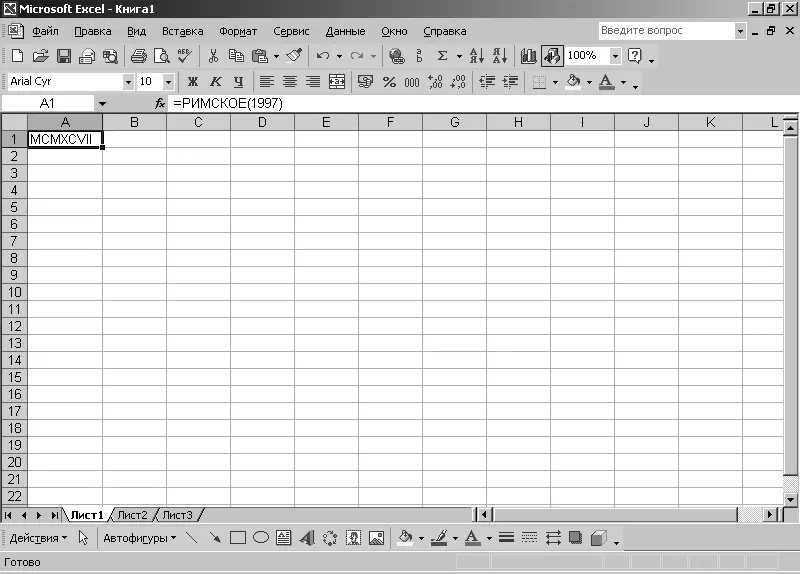
Рис. 2.4. Лист MS Excel «Результат преобразований»

Наибольшее применение при вводе, обработке и выводе информации в компьютере и компьютерных системах нашли позиционные системы счисления, при этом самыми распространенными являются десятичная, двоичная, восьмеричная и шестнадцатеричная системы. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Основание системы равно количеству цифр (знаков ее алфавита) и определяет, во сколько раз различаются значения цифр соседних разрядов числа. В общем случае в позиционной системе счисления любое число, содержащее целую и дробные части, в развернутой форме может быть представлено в виде:

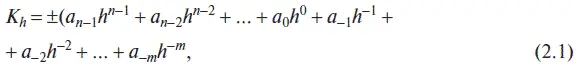
или в рекуррентной форме:

где K – представляемое число; h – основание системы счисления; а – разрядный коэффициент, а = 0, 1, 2, 3…, h-1 , т. е. цифры, принадлежащие алфавиту данной системы счисления; i – номер разряда, позиция; п – число целых разрядов числа; т – число дробных разрядов числа.

В десятичной системе счисления формула (2.2) может быть записана следующим образом:

где а = 0, 1, 2, 3…, 9.

Например, число 827 десятичной системы счисления в соответствии с выражением (2.3) можно представить в виде: 827 = 8 · 10 2+ 2 · 10 1+ 7 · 10 0.

Десятичная система исчисления используется в компьютерах для ввода числовых данных и отображения полученного результата. Все внутренние, промежуточные операции компьютер производит в двоичной системе счисления и соотношение (2.2) примет вид:

где а = 0, 1.

Например, число 1100111011 2двоичной системы счисления в соответствии с формулой (2.4) можно представить в виде: 1 · 2 9+ 1 · 2 8+ 0 · 2 7+ 0 · 2 6+ 1 · 2 5+ 1 · 2 4+ 1 · 2 3+ 0 · 2 2+ 1 · 2 1+ 1 · 2 0.

Достаточно широко при компьютерной обработке информации применяются восьмеричная и шестнадцатеричная системы счисления, которые используются, например, для обозначения адресов расположения данных в памяти компьютера и т. д.

Соотношение (2.2) для восьмеричной и шестнадцатеричной системы счисления соответственно примет вид (2.5) и (2.6) :

где а = 0, 1, 2, 3…, 7.

Например, число 1473 8восьмеричной системы счисления в соответствии с (2.5) примет вид: 1 · 8 3+ 4 · 8 2+ 7 · 8 1+ 3 · 8 0.

где а = 0, 1, 2, 3…, 9, A, B, C, D, E, F.

В шестнадцатеричной системе счисления используется шестнадцать цифр, из которых десять цифр арабские (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а остальные цифры (10, 11, 12, 13, 14, 15) обозначаются буквами латинского алфавита (А = 10, В = 11, С = 12, D = 13, E = 14, F = 15).

Например, число 33B 16шестнадцатеричной системы счисления, в соответствии с (2.6) примет вид: 3 · 16 2+ 3 · 16 1+ В · 16 0 (В = 11).

При операциях с числами, представленными в различных системах счисления, необходимо указывать систему счисления числа, используя нижний индекс, например: 827 10– число 827 в десятичной системе; 1100111011 2– число 1100111011 в двоичной системе; 1473 8– число 1473 в восьмеричной системе; 33B 16– число 33В в шестнадцатеричной системе счисления.

Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную осуществляется достаточно просто. Для этого необходимо записать число в развернутой форме в соответствии с выражением (2.1) и вычислить его значение. Например:

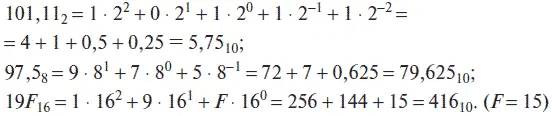
Преобразование чисел, представленных в десятичной системе счисления, в двоичную, восьмеричную и шестнадцатеричную системы счисления – более сложная процедура, которая может осуществляться различными способами: деления, умножения, вычитания и т. д. При этом необходимо учитывать, что способы перевода целых десятичных чисел и правильных дробей будут различаться. Для перевода целого десятичного числа, например 53 10, в двоичную систему можно использовать способ деления, а десятичной правильной дроби, например 0,75 10, в двоичную систему – способ умножения. Результаты действий отобразим в соответствующих табл. 2.1 и 2.2.