Владимир Яшин - Информатика: аппаратные средства персонального компьютера

1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;

2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);

3) к полученному обратному коду прибавить единицу к младшему разряду.

Например, для числа -536 10в таком формате модуль будет равен 0000001000011000 2, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536 10, т. е. число 536 10, и с помощью опционной кнопки Binпреобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта.Нажав кнопку Notкалькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536 10и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.

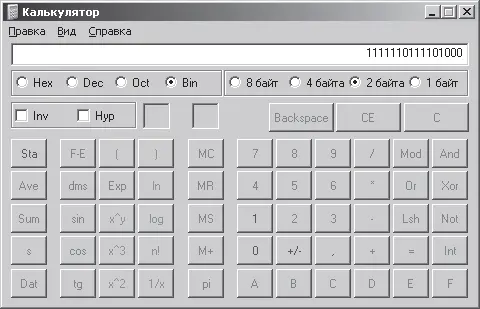
Рис. 2.6. Результат получения дополнительного кода

Необходимо помнить, что дополнительный код положительного числа – само число.

Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 31 – 1) … + 2 31– 1 и -(2 63-1) … + 2 63– 1.

Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).

Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.

Выражение (2.7) для десятичной системы счисления примет вид:

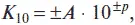
для двоичной —

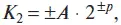
для восьмеричной —

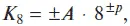
для шестнадцатеричной —

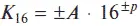
и т. д.

Такая форма представления числа также называется нормальной. С изменением порядка запятая в числе смещается, т. е. как бы плавает влево или вправо. Поэтому нормальную форму представления чисел называют формой с плавающей запятой. Десятичное число 15,5, например, в формате с плавающей запятой может быть представлено в виде: 0,155 · 10 2; 1,55 · 10 1; 15,5 · 10 0; 155,0 · 10 -1; 1550,0 · 10 -2и т. д. Эта форма записи десятичного числа 15,5 с плавающей запятой не используется при написании компьютерных программ и вводе их в компьютер (устройства ввода компьютеров воспринимают только линейную запись данных). Исходя из этого выражение (2.7) для представления десятичных чисел и ввода их в компьютер преобразовывают к виду

где Р – порядок числа,

т. е. вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, и знак умножения не ставится. Таким образом, число 15,5 в формате с плавающей запятой и линейной записи (компьютерное представление) будет записано в виде: 0.155Е2; 1.55Е1; 15.5Е0; 155.0Е-1; 1550.0Е-2 и т.д.

Независимо от системы счисления любое число в форме с плавающей запятой может быть представлено бесконечным множеством чисел. Такая форма записи называется ненормализованной. Для однозначного представления чисел с плавающей запятой используют нормализованную форму записи числа, при которой мантисса числа должна отвечать условию

где |А| — абсолютное значение мантиссы числа.

Условие (2.9) означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля, или, другими словами, если после запятой в мантиссе стоит не нуль, то число называется нормализованным. Так, число 15,5 в нормализованном виде (нормализованная мантисса) в форме с плавающей запятой будет выглядеть следующим образом: 0,155 · 10 2, т. е. нормализованная мантисса будет A = 0,155 и порядок Р = 2, или в компьютерном представлении числа 0.155Е2.

Числа в форме с плавающей запятой имеют фиксированный формат и занимают в памяти компьютера четыре (32 бит) или восемь байт (64 бит). Если число занимает в памяти компьютера 32 разряда, то это число обычной точности, если 64 разряда, то это число двойной точности. При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, мантиссы и порядка. Количество разрядов, которое отводится под порядок числа, определяет диапазон изменения чисел, а количество разрядов, отведенных для хранения мантиссы, – точность, с которой задается число.

При выполнении арифметических операций (сложение и вычитание) над числами, представленными в формате с плавающей запятой, реализуется следующий порядок действий (алгоритм) :

1) производится выравнивание порядков чисел, над которыми совершаются арифметические операции (порядок меньшего по модулю числа увеличивается до величины порядка большего по модулю числа, мантисса при этом уменьшается в такое же количество раз);

2) выполняются арифметические операции над мантиссами чисел;