Владимир Большаков - КОМПАС-3D для студентов и школьников. Черчение, информатика, геометрия

Правильная призма — это прямая призма, у которой основания — правильные многоугольники.

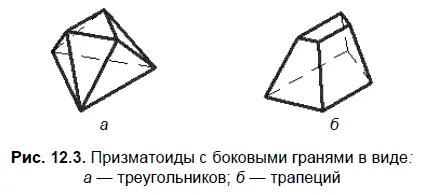
Призматоид — многогранник, у которого параллельные основания являются многоугольниками с произвольным числом углов, боковые грани — треугольники (рис. 12.3, а ) или трапеции (рис. 12.3, б ).

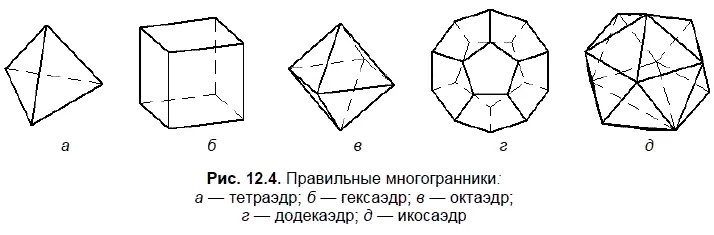
Правильные многогранники имеют все грани в виде правильных и конгруэнтных многоугольников, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней.

Гранями правильных многогранников могут быть только правильные треугольники, четырехугольники и пятиугольники. Одной из особенностей правильных многогранников является то, что каждый из них вписывается в сферу. Примерами правильных многогранников являются:

□ тетраэдр — правильный четырехгранник (рис. 12.4, а );

□ гексаэдр — правильный шестигранник (рис. 12.4, б );

□ октаэдр — правильный восьмигранник (рис. 12.4, в );

□ додекаэдр — правильный двенадцатигранник (рис. 12.4, г );

□ икосаэдр — правильный двадцатигранник (рис. 12.4, д ).

Рассмотрим примеры 3D-моделирования правильных многогранников.

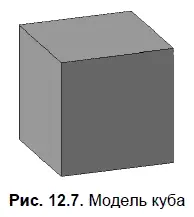
Условие. Создать твердотельную модель куба (см. рис. 12.4, б).

Решение. Модель куба получим в результате выдавливания квадрата на расстояние, равное его стороне.

1. Для создания модели выполните команду Файл | Создатьили нажмите кнопку Создатьна панели Стандартная:

В открывшемся окне выберите тип нового документа Деталь.

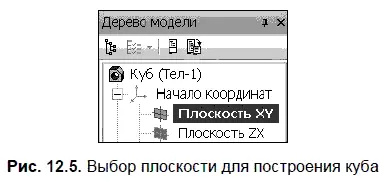
В Дереве модели укажите Плоскость XY. Введите название модели — Куб(рис. 12.5).

2. Нажмите кнопку Эскизна панели Текущее состояние:

Плоскость ху станет параллельной экрану.

3. В появившейся Компактной панелинажмите кнопку переключения Геометриядля вызова соответствующей Инструментальной панели:

4. На панели Глобальные привязкивключите привязку По сетке, а также включите изображение сетки на экране. Выберите команду Прямоугольник по центру и вершинена Инструментальной панели режима Геометрия:

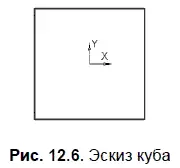
5. Укажите точку — центр квадрата. Постройте квадрат со стороной, например, 50 мм (рис. 12.6).

Заканчивается эскиз повторным нажатием кнопки Эскиз:

6. Нажмите кнопку Операция выдавливания:

на панели Редактирование детали:

Внизу экрана появится Панель свойств, на которой установите параметры выдавливания: Прямое направление; Расстояние 1 — 50.0. Ввод параметров заканчивается нажатием кнопки Создать объект:

7. После включения Ориентация | Диметрияи команды Полутоновое изображениена панели Видполучится показанное на рис. 12.7 изображение куба.

Условие. Создать твердотельную модель тетраэдра (см. рис. 12.4, а ).

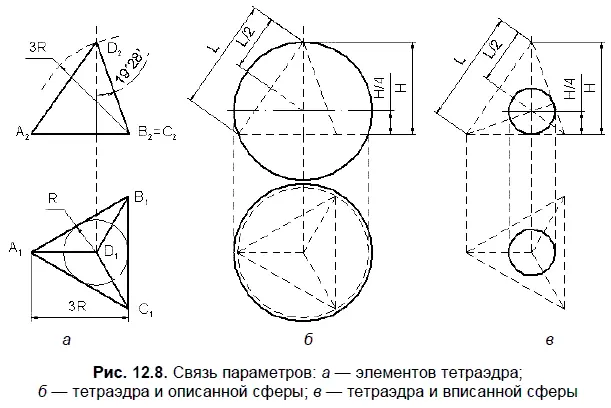
Решение. На рис. 12.8, а показаны две проекции тетраэдра с указанием связи между его основными параметрами, на рис. 12.8, б — проекции тетраэдра и описанной вокруг него сферы, а на рис. 12.8, в — проекции тетраэдра и вписанной сферы.

Модель тетраэдра создадим по сечениям. Первое сечение — основание тетраэдра, построенное, например, по величине радиуса R вписанной окружности. Вторым сечением будет вершина D , положение которой определяется известными соотношениями (рис. 12.8, а ).

В табл. 12.2 описаны действия, необходимые для создания 3D-модели тетраэдра.

1. Для создания модели выполните команду Файл | Создатьили нажмите кнопку Создатьна панели Стандартная:

В открывшемся окне выберите тип нового документа Деталь.

2. В Дереве модели укажите Плоскость ХY. Введите название модели — Тетраэдр(рис. 12.9).

3. Нажмите кнопку Эскизна панели Текущее состояние:

Плоскость ху станет параллельной экрану.

4. В появившейся Компактной панелинажмите кнопку переключения Геометриядля вызова соответствующей Инструментальной панели:

5. Выберите команду Многоугольник:

В Панели свойств укажите количество вершин многоугольника — 3.

6. Укажите точку центра многоугольника. Постройте треугольник по диаметру вписанной окружности, равному, например, 30 мм (рис. 12.10).

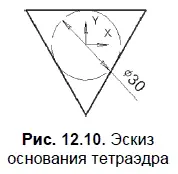
Заканчивается эскиз повторным нажатием кнопки Эскиз:

7. В Дереве модели укажите Плоскость ZY. Нажмите кнопку Эскизна панели Текущее состояние:

Выполните команды Операции | Спроецировать объекти укажите ребро основания. Измените стиль линии спроецированного отрезка. Проведите горизонтальную ось из начала координат и дугу R45 с центром в начале спроецированного отрезка (стиль Основнаяне использовать) — рис. 12.11.