Александр Леоненков - Самоучитель UML

Рядом со стрелкой обобщения может размещаться строка текста, указывающая на некоторые дополнительные свойства этого отношения. Данный текст будет относиться ко всем линиям обобщения, которые идут к классам-потомкам. Другими словами, отмеченное свойство касается всех подклассов данного отношения. При этом текст следует рассматривать как ограничение, и тогда он записывается в фигурных скобках.

В качестве ограничений могут быть использованы следующие ключевые слова языка UML:

• {complete} – означает, что в данном отношении обобщения специфицированы все классы-потомки, и других классов-потомков у данного класса-предка быть не может. Пример – класс Клиент_банка является предком для двух классов: Физическое_лицо и Компания, и других классов-потомков он не имеет. На соответствующей диаграмме классов это можно указать явно, записав рядом с линией обобщения данную строку-ограничение;

• {disjoint} – означает, что классы-потомки не могут содержать объектов, одновременно являющихся экземплярами двух или более классов. В приведенном выше примере это условие также выполняется, поскольку предполагается, что никакое конкретное физическое лицо не может являться одновременно и конкретной компанией. В этом случае рядом с линией обобщения можно записать данную строку-ограничение;

• {incomplete} – означает случай, противоположный первому. А именно, предполагается, что на диаграмме указаны не все классы-потомки. В последующем возможно восполнить их перечень не изменяя уже построенную диаграмму. Пример – диаграмма класса «Автомобиль», для которой указание всех без исключения моделей автомобилей соизмеримо с созданием соответствующего каталога. С другой стороны, для отдельной задачи, такой как разработка системы продажи автомобилей конкретных моделей, в этом нет необходимости. Но указать неполноту структуры классов-потомков все же следует;

• {overlapping} – означает, что отдельные экземпляры классов-потомков могут принадлежать одновременно нескольким классам. Пример – класс «Многоугольник» является классом-предком для класса «Прямоугольник» и класса «Ромб». Однако существует отдельный класс «Квадрат», экземпляры которого одновременно являются объектами первых двух классов. Вполне естественно такую ситуацию указать явно с помощью данной строки-ограничения.

С учетом возможности использования строк-ограничений диаграмма классов (рис. 5.14) может быть изображена без многоточий и без потери информации (рис. 5.15).

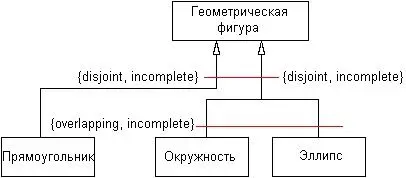
Рис. 5.15.Вариант графического изображения отношения обобщения классов с использованием строки-ограничения

Чтобы проиллюстрировать особенности использования отношения обобщения, преобразуем один из рассмотренных ранее примеров изображения классов в графическую нотацию языка UML. В качестве такого примера рассмотрим иерархию вложенности классов для абстрактного класса «Автомобиль» (см. рис. 1,2, 2.7). Как нетрудно заметить, отношение между отдельными классами на этих рисунках есть именно отношение обобщения, которое в языке UML имеет специальное графическое обозначение. С учетом этой графической нотации, фрагмент семантической сети для представления иерархии класса «Автомобиль» (см. рис. 2.7) может быть представлен в виде следующей диаграммы классов (рис. 5.16).

Заметим, что в данном примере все классы верхних уровней являются абстрактными, т. е. не могут быть представлены своими экземплярами. Именно поэтому их имена записаны курсивом. В отличие от них классы нижнего уровня являются конкретными, поскольку могут быть представлены своими экземплярами, в качестве которых выступают изготовленные автомобили соответствующей модели с уникальным заводским номером.

Рис. 5.16.Фрагмент диаграммы классов с отношением обобщения для представления иерархии классов «Автомобиль» из рассмотренного ранее примера (см. рис. 2.7)

Примечание 49 Примечание 49 В качестве упражнения для закрепления рассмотренного материала можно попытаться построить диаграммы классов или хотя бы их фрагменты для библиотек стандартных классов MFC (Microsoft) и VCL (Borland/Inprise) с использованием графической нотации языка UML. Можно предположить, что в недалеком будущем справочные руководства по соответствующим средам программирования будут содержать именно такие диаграммы классов, а возможно, и некоторые другие.

Интерфейсы являются элементами диаграммы вариантов использования и были рассмотрены в главе 4. Однако при построении диаграммы классов отдельные интерфейсы могут уточняться и в этом случае для их изображения используется специальный графический символ – прямоугольник класса с ключевым словом или стереотипом «interface» (рис. 5.17). При этом секция атрибутов у прямоугольника отсутствует, а указывается только секция операций.

Рис. 5.17.Пример графического изображения интерфейса на диаграмме классов

Объект (object) является отдельным экземпляром класса, который создается на этапе выполнения программы. Он имеет свое собственное имя и конкретные значения атрибутов. В силу самых различных причин может возникнуть необходимость показать взаимосвязи не только между классами модели, но и между отдельными объектами, реализующими эти классы. В данном случае может быть разработана диаграмма объектов, которая, хотя и не является канонической в метамодели языка UML, но имеет самостоятельное назначение.

Для графического изображения объектов используется такой же символ прямоугольника, что и для классов. Отличия проявляются при указании имен объектов, которые в случае объектов обязательно подчеркиваются (рис. 5.18). При этом запись имени объекта представляет собой строку текста «имя объекта:имя класса», разделенную двоеточием (рис. 5.18 а, б). Имя объекта может отсутствовать, в этом случае предполагается, что объект является анонимным, и двоеточие указывает на данное обстоятельство (рис. 5.18, г). Отсутствовать может и имя класса. Тогда указывается просто имя объекта (рис. 5.18, в). Атрибуты объектов принимают конкретные значения.

При изображении диаграммы объектов нужно помнить, что каждый объект представляет собой экземпляр соответствующего класса, а отношения между объектами описываются с помощью связей (links), которые являются экземплярами соответствующих отношений. При этом все связи изображаются сплошными линиями. Более подробно особенности представления объектов будут рассмотрены в главе 9 при изучении диаграмм кооперации.