Олег Деревенец - Песни о Паскале

Б) В пору расцвета континента все страны установили между собой дипломатические отношения. Нарисуйте подобающий граф.

В) В период политического кризиса соседние страны перессорились между собой и разорвали дипломатические отношения. Какие ребра графа уцелели? Нарисуйте его.

Г) Пусть названия стран представляются не буквами, а словами. Возьмите карту Европы и создайте входной файл для нескольких соседних стран, например:

Франция Испания Италия Бельгия Швейцария

Италия Франция Швейцария Словения

и так далее, перечисляя страны-соседи и отделяя их одним или несколькими пробелами. Напишите программу для ввода и вывода такого графа. Что придется изменить в структуре узла?

Ознакомившись с графами, вернемся к программисту Нику, который все ещё царапает прибрежный песочек. «Если бы, – бормочет Ник, – мне надо было попасть из страны «E» в страну «H», то я бы поехал так». И он прочертил жирные стрелки, ведущие к цели через узлы «F» и «G» (рис. 138). «Но это я сообразил, глядя на карту, а без карты можно блуждать вот так», – и нацарапал стрелки, показанные пунктиром.

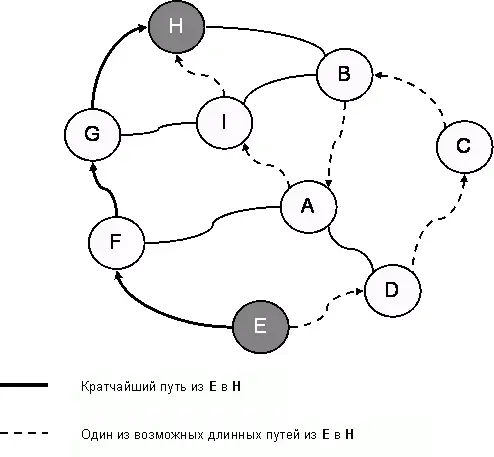
Как растолковать компьютеру верный путь? Нужна свежая идея! Новое – это всего лишь забытое старое – почему-то вспомнилось ему. «А не построить ли тебе здесь империю, как ты сделал это в 49-й главе?» – шепнул Нику внутренний голос. И мысли программиста двинулись в этом направлении.

Друзья, что вы слышали о постройке нынешних империй? Ведь на дворе не лютое средневековье! К чему проливать кровь, если от желающих нет отбоя, и очередь на присоединение к империям не пустует? Очередь упомянута мною не зря, – она играет важную роль в будущем алгоритме. Кстати, алгоритм этот придумали не программисты, а политики. Судите сами, сейчас вместе с Ником мы последуем их примеру.

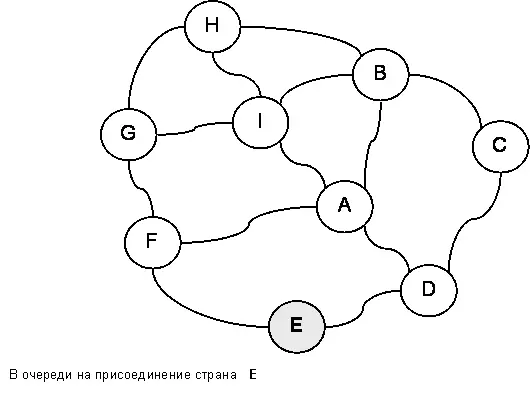
На рис. 139 показан граф в начале строительства «империи» (дальше я пишу это слово без кавычек). Условимся об окраске его узлов. Все страны континента (узлы) отнесем к трем категориям: 1) независимые страны, 2) страны, желающие присоединиться к империи и 3) страны, вошедшие в её состав. Независимые страны окрасим белым цветом, желающие присоединиться – серым, а присоединенные к империи – черным.

Откуда начать строительство? Пусть центром империи будет страна «E». Окрасим её серым цветом и поставим в очередь на присоединение. Можно сказать, что страна «E» – первый кандидат на включение в несуществующую пока империю.

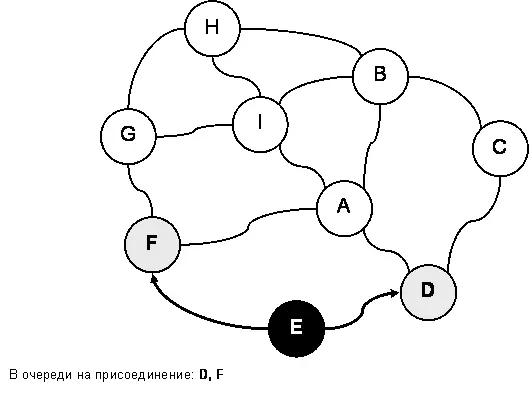
Серому кандидату поставим жесткое условие: хочешь быть принятым в империю и почернеть? Тогда уговори своих белых соседей тоже стать в очередь на присоединение и перекраситься в серый цвет. Так, страну «E» примут в империю, когда кандидатами на присоединение станут царства «D» и «F», что и показано на рис. 140. Кандидат, выполнивший это условие, удаляется из очереди на присоединение и включается в империю – чернеет.

К слову сказать, строя империю, Ник постоянно думал о купцах. Жирными стрелками на графе он помечал их воображаемое движение, как если бы купцы шли вослед завоевателям.

Итак, страна «E» вошла в империю, а два её соседа – «D» и «F» – стали в очередь на присоединение (в каком именно порядке – «D», затем «F» или наоборот – неважно). От них требуют то же самое – уговорить своих белых соседей. Так, для присоединения страны «D» ей надо убедить стать в очередь страны «A» и «C». По мере выполнения этого условия страны-кандидаты чернеют и удаляются из очереди. После двух следующих присоединений (стран «D» и «F») граф и очередь изменятся так, как показано на рис. 141 и рис. 142. Здесь же стрелками показано и воображаемое продвижение купцов.

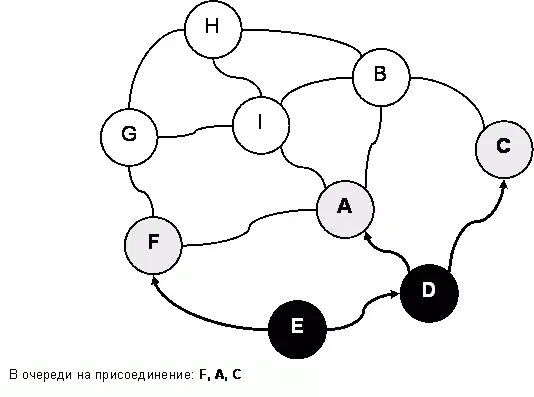
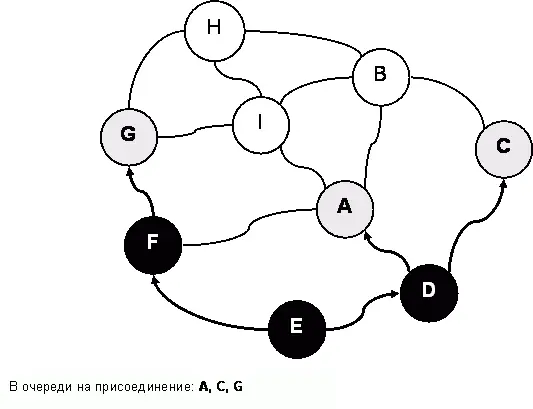
Итак, строительство двинулось, но когда оно закончится? Очевидно, что страны с окраин империи рано или поздно войдут в число желающих, то есть, станут серыми, и тогда не останется белых соседей. А раз так, то очередь на присоединение постепенно опустеет, все страны почернеют, и строительство империи прекратится.

«Хорошо, – скажете, – только, причем тут поиск кратчайшего пути?». Но мы ведь не зря пустили купцов вослед завоевателям! Если купец потянет за собой ниточку, исходящую из начального узла «E», то из любого узла империи сможет вернуться к началу, следуя по нити в обратном направлении (Рис. 143).

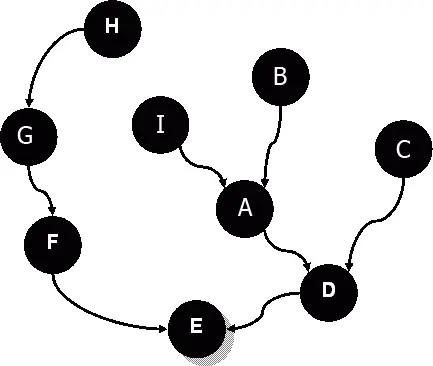
Ник догадался, что путь из любого узла графа вдоль этих ниточек к исходной точке будет кратчайшим. Это следует из того, что империя расширялась присоединением ближайших соседей. Действительно, узлы «D» и «F» – ближайшие к исходному узлу «E», ведь они его соседи. Точно так же узел «G» – ближайший к узлу «F», а узел «H» – ближайший к узлу «G». Эти рассуждения справедливы для любых ниточек обратных связей.

Цепочки обратных связей тоже образуют граф, называемый деревом. Программисты часто применяют деревья, основное свойство которых состоит в наличии единственного пути между любыми узлами. Узел, из которого начато строительство дерева, является его корнем – это центр построенной нами империи (не географический, а политический центр).

Итак, строительство империи породило дерево обратных связей. Но как организовать эти ниточки? Введем в структуру узла ещё одно поле – указатель на узел, из которого мы пришли сюда по ходу расширения империи. Назовем это поле mPrev – предыдущий. Например, для узлов «F» и «D» предыдущим будет узел «E».