Олег Деревенец - Песни о Паскале
- Название:Песни о Паскале
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Олег Деревенец - Песни о Паскале краткое содержание
Песни о Паскале - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Что ж, дело нехитрое, сейчас посчитаем, – перед вами программа для наших опытов («P_43_3»). Количество сравнений и перестановок будем накапливать в переменных C1 и C2. Обратите внимание на их тип – EXTENDED, – это переменные действительного типа. Почему не длинное целое? При сортировке больших массивов может потребоваться столь много операций, что не хватит целочисленной переменной, – она переполнится, «лопнет», и результат исказится. Потому выбран тип EXTENDED.
Далее в программе следуют знакомые вам процедуры сортировки, – это наши «спортсмены». В их тела «вживлены» дополнительные операторы для подсчета сравнений (C1) и перестановок (C2), – они выделены курсивом. Наконец, главная программа, – она вызывает по очереди каждую из процедур и печатает количество сравнений и перестановок. Здесь равные условия для соревнующихся создаются загодя сформированным случайным массивом Arr0, который копируется в массив Arr перед каждой сортировкой.
Вам осталось лишь задать размер массива константой CSize, скомпилировать и запустить программу.
{ P_43_3 – Сравнение алгоритмов сортировки }
const CSize=100; { размер массивов }
type TNumbers = array [1..CSize] of Integer;
var Arr0 : TNumbers; { несортированный массив-заготовка }
Arr : TNumbers; { сортируемый массив }
C1, C2 : extended; { счетчики сравнений и перестановок }
{ BubbleSort "пузырьковая" сортировка }
procedure BubbleSort(var arg: TNumbers);
var i, j, t: Integer;
begin
for i:= 1 to CSize-1 do
for j:= 1 to CSize-i do begin
C1:=C1+1; { подсчет сравнений }
if arg[j] > arg[j+1] then begin
C2:=C2+1; { подсчет перестановок }
t:= arg[j]; arg[j]:= arg[j+1]; arg[j+1]:= t;
end;
end;
end;
{ FarmSort – «Фермерская» сортировка }
procedure FarmSort(var arg: TNumbers);
var L, R, T: Integer;
begin
for L := 1 to CSize-1 do
for R := CSize downto L+1 do begin
C1:=C1+1; { подсчет сравнений }
if arg[L] > arg[R] then begin
C2:=C2+1; { подсчет перестановок }
T:= arg[L]; arg[L]:= arg[R]; arg[R]:= T;
end;
end;
end;
{ QuickSort – Быстрая сортировка }
procedure QuickSort(var arg: TNumbers; aL, aR: Integer);
var
L, R, Mid, T: Integer;
begin
L:= aL; R:= aR;
Mid:= (arg[L] + arg[(L + R) div 2] + arg[R]) div 3;
repeat
while arg[L] < Mid do begin L:=L+1; C1:=C1+1 end;
while arg[R] > Mid do begin R:=R-1; C1:=C1+1 end;
if L <= R then begin
if arg[L]>arg[R] then begin
C2:=C2+1; { подсчет перестановок }
t:= arg[L]; arg[L]:= arg[R]; arg[R]:= t;
end;
L:=L+1; R:=R-1;
end;
until L > R;
if R > aL then QuickSort(arg, aL, R);
if L < aR then QuickSort(arg, L, aR);
end;
const CFName = 'P_43_3.out';
var i: integer;
F: text;
begin
Assign(F,CFName); Rewrite(F);
for i:=1 to CSize do Arr0[i]:=1+Random(10000);
Writeln(F, 'Размер массива = ', CSize);
Writeln(F, 'Алгоритм Количество Количество');
Writeln(F, 'сортировки сравнений перестановок');
C1:=0; C2:=0; { очистить счетчики }
Arr:= Arr0; { заполнить сортируемый массив }
BubbleSort(Arr);
Writeln(F, 'Пузырьковая:', C1:12:0, C2:12:0);
C1:=0; C2:=0; { очистить счетчики }
Arr:= Arr0; { заполнить сортируемый массив }
FarmSort(Arr);
Writeln(F, 'Фермерская :', C1:12:0, C2:12:0);
C1:=0; C2:=0; { очистить счетчики }
Arr:= Arr0; { заполнить сортируемый массив }
QuickSort(Arr, 1, CSize);
Writeln(F, 'Быстрая :', C1:12:0, C2:12:0);
Writeln('OK !'); Readln;
Close(F);
end.
Вот что получилось для массива из 1000 элементов.
Размер массива = 1000
Алгоритм Количество Количество
сортировки сравнений перестановок
Пузырьковая: 499500 248061
Фермерская : 499500 80887
Быстрая : 5871 2417
Я провел три опыта с массивами из 100, 1000 и 10000 элементов, а результаты занес в две таблички. Что сказать по этому поводу?
Табл. 9 – Количество сравнений в разных методах сортировки
| Размер массива | «Пузырьковая» сортировка | «Фермерская» сортировка | Быстрая сортировка |
| 100 | 4 950 | 4 950 | 417 |
| 1 000 | 499 500 | 499 500 | 5 871 |
| 10 000 | 49 995 000 | 49 995 000 | 79 839 |
Из табл. 9 следует, что по количеству сравнений «Фермерская» сортировка не лучше «пузырька». Зато быстрая сортировка оправдывает свое название, – выигрыш составляет от 10 до 600 раз! И чем больше массив, тем заметней этот разрыв.
Табл. 10 – Количество перестановок в разных методах сортировки
| Размер массива | Пузырьковая сортировка | Фермерская сортировка | Быстрая сортировка |
| 100 | 2 305 | 805 | 141 |
| 1 000 | 248 061 | 80 887 | 2 417 |
| 10 000 | 24 903 994 | 6 154 077 | 31 011 |
А что с количеством перестановок (табл. 2)? Здесь «фермерская» сортировка всё же в 3—4 раза обгоняет «пузырёк». Так что фермеру Лефту в сметливости не откажешь. И всё же этому «спортсмену» далеко до изобретения Райта! В сравнении с «пузырьком» выигрыш стократный, и стремительно растёт с ростом размера массива. Слава, слава фермеру Райту! Кстати, историки выяснили его настоящее имя: это англичанин Чарльз Хоар.

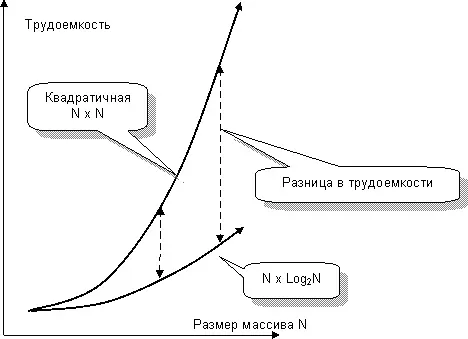
Итак, с чемпионом все ясно (рис. 96), но в чем секрет его успеха? Сравним чемпиона с отставшими. Чем больше массив, тем дольше он сортируется, – это справедливо для любого алгоритма. Долгие методы обрабатывают весь массив N раз, где N – размер массива. Поэтому их трудоемкость пропорциональна произведению N•N. По этой формуле вычисляют площадь квадрата, и такую зависимость называют квадратичной.
Иное дело – чемпион. Дробя массив на мелкие участки, быстрый алгоритм уменьшает число прохождений всего массива до величины Log 2N. Поэтому его трудоемкость растёт пропорционально произведению N•Log 2N. Опять логарифм? Да, мы помним его по двоичному поиску. Поскольку логарифм числа растёт очень медленно, это объясняет чемпионство QuickSort (рис. 97).
• Двоичный поиск – это самый быстрый способ поиска, но он требует предварительной сортировки массива.
Читать дальшеИнтервал:
Закладка:









