Коллектив Авторов - Базы данных: конспект лекций

Операция полного внешнего соединенияопределяется как результат пополнения того же самого внутреннего соединения (как и в случае определения левого и правого внешних соединений) несоединимыми кортежами одновременно и левого, и правого исходных отношений-операндов. Исходя из этого определения дадим формулярный вид этого определения:

r 1( S 1) ↔× P r 2( S 2) = ( r 1→× P r 2) ∪ ( r 1←× P r 2) ;

У операции полного внешнего соединения также имеется свойство, сходное с аналогичным свойством операций левого и правого внешних соединений. Только за счет изначальной взаимно-обратной природы операции полного внешнего соединения (ведь она была определена как объединение операций левого и правого внешних соединений) для нее выполняется свойство коммутативности:

r 1( S 1) ↔× P r 2( S 2) = r 2( S 2) ↔ × P r 1( S 1);

И для завершения рассмотрения вариантов операций соединения, рассмотрим пример, иллюстрирующий работу операции полного внешнего соединения. Введем два отношения r 1( S 1) и r 2( S 2) и условие соединения.

Пусть

r 1( S 1)

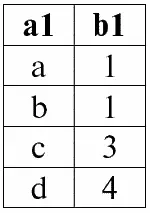
r 2( S 2):

И пусть условием соединения отношений r 1( S 1) и r 2( S 2) будет: P = (b1 = b2), как и в предыдущих примерах.

Тогда результатом операции полного внешнего соединения отношений r 1( S 1) и r 2( S 2) по условию P = (b1 = b2) будет следующая таблица:

r 1( S 1) ↔× P r 2( S 2):

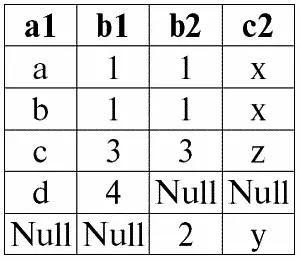
Итак, мы видим, что операция полного внешнего соединения наглядно оправдала свое определение как объединения результатов операций левого и правого внешних соединений. Результирующее отношение операции внутреннего соединения дополнено одновременно несоединимыми кортежами как левого (первого, r 1( S 1)), так и правого (второго, r 2( S 2)) исходного отношения-операнда.

Итак, мы рассмотрели различные варианты операций соединения, а именно операции внутреннего соединения, левого, правого и полного внешнего соединения, которые являются производными восьми исходных операций реляционной алгебры: унарных операций выборки, проекции, переименования и бинарных операций объединения, пересечения, разности, декартова произведения и естественного соединения. Но и среди этих исходных операций есть свои примеры производных операций.

1. Например, операция пересечениядвух отношений является производной от операции разности этих же двух отношений. Покажем это.

Операцию пересечения можно выразить следующей формулой:

r 1( S ) ∩ r 2( S ) = r 1\ r 1\ r 2

или, что дает тот же результат:

r 1( S ) ∩ r 2( S ) = r 2\ r 2\ r 1;

2. Еще одним примером, производной базовой операции от восьми исходных операций является операция естественного соединения. В самом общем виде эта операция является производной от бинарной операции декартового произведения и унарных операций выборки, проекции и переименования атрибутов. Однако, в свою очередь, операция внутреннего соединения является производной операцией от той же операции декартового произведения отношений. Поэтому, чтобы показать, что операция естественного соединения – производная операция, рассмотрим следующий пример.

Сравним приведенные ранее примеры для операций естественного и внутреннего соединений.

Пусть нам даны два отношения r 1( S 1) и r 2( S 2) которые будут выступать в качестве операндов. Они равны:

r 1( S 1):

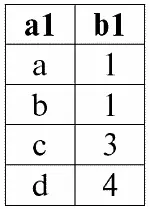
r 2( S 2):

Как мы уже получали ранее, результатом операции естественного соединения этих отношений будет являться таблица следующего вида:

r 3( S 3) ≔ r 1( S 1) × r 2( S 2):

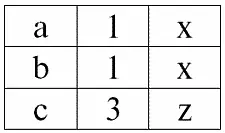
А результатом внутреннего соединения этих же отношений r 1( S 1) и r 2( S 2) по условию P = (b1 = b2) будет следующая таблица:

r 4( S 4) ≔ r 1( S 1) × P r 2( S 2):

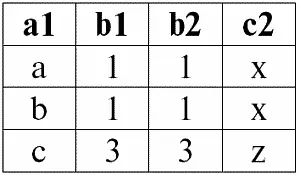
Сравним эти два результата, получившиеся новые отношения r 3( S 3) и r 4( S 4).

Ясно, что операция естественного соединения выражается через операцию внутреннего соединения, но, что главное, с условием соединения специального вида.

Запишем математическую формулу, описывающую действие операции естественного соединения как производную операции внутреннего соединения.

r 1( S 1) × r 2( S 2) = { ρ < ϕ 1> r 1× E ρ < ϕ 2> r 2}[ S 1 ∪ S 2],

где E — условие соединимостикортежей;

E = ∀ a ∈ S 1∩ S 2[ IsNull ( b 1) & IsNull (2) ∪ b 1 = b 2];

b 1= ϕ 1( name ( a )) , b 2= ϕ 2( name ( a ));

Здесь одна из функций переименования ϕ 1является тождественной, а другая функция переименования (а именно – ϕ 2) переименовывает атрибуты, на которых наши схемы пересекаются.

Условие соединимости E для кортежей записывается в общем виде с учетом возможных появлений Null-значений, ведь операция внутреннего соединения (как уже было сказано выше) является производной операцией от операции декартового произведения двух отношений и унарной операции выборки.

Покажем, как можно использовать рассмотренные ранее выражения и операции реляционной алгебры в практической эксплуатации различных баз данных.

Пусть для примера в нашем распоряжении имеется фрагмент какой-то коммерческой базы данных: