Коллектив Авторов - Базы данных: конспект лекций

r 1× r 2= r 2× r 1.

Свойство коммутативности выполняется для всех операций, кроме операции разности. Это легко понять, ведь от перестановки отношений местами их состав (кортежи) не меняется. А при применении операции разности важно, какое из отношений-операндов стоит на первом месте, потому что от этого зависит, кортежи какого отношения примутся за эталонные, т. е. с какими кортежами будут сравниваться другие кортежи на предмет исключения.

4. Свойство ассоциативности:

1) для операции объединения:

( r 1∪ r 2) ∪ r 3= r 1∪( r 2∪ r 3) ;

2) для операции пересечения:

( r 1∩ r 2) ∩ r 3= r 1∩ ( r 2∩ r 3);

3) для операции разности:

( r 1\ r 2) \ r 3≠ r 1\ ( r 2\ r 3);

4) для операции декартового произведения:

( r 1× r 2) × r 3= r 1× ( r 2× r 3);

5) для операции естественного соединения:

( r 1× r 2) × r 3= r 1× ( r 2× r 3).

И снова мы видим, что свойство выполняется для всех операций, кроме операции разности. Объясняется это таким же образом, как и в случае применения свойства коммутативности. По большому счету, операциям объединения, пересечения, разности и естественного соединения все равно в каком порядке стоят отношения-операнды. Но при «отнимании» отношений друг от друга порядок играет главенствующую роль.

На основании вышеприведенных свойств и рассуждений можно сделать следующий вывод: три последних свойства, а именно свойство идемпотентности, коммутативности и ассоциативности, верны для всех рассмотренных нами операций, кроме операции разности двух отношений, для которой не выполнилось вообще ни одно из трех означенных свойств, и только в одном случае свойство оказалось неприменимым.

Используя как основу рассмотренные ранее унарные операции выборки, проекции, переименования и бинарные операции объединения, пересечения, разности, декартова произведения и естественного соединения (все они в общем случае называются операциями соединения), мы можем ввести новые операции, выведенные с помощью перечисленных понятий и определений. Подобная деятельность называется составлением вариантов операций соединения.

Первым таким вариантом операций соединения является операция внутреннего соединенияпо заданному условию соединения.

Операция внутреннего соединения по какому-то определенному условию определяется как производная операция от операций декартового произведения и выборки.

Запишем формульное определение этой операции:

r 1( S 1) × P r 2( S 2) = σ < P > ( r 1× r 2), S 1∩ S 2= ∅;

Здесь P = P < S 1∪ S 2> – условие, накладываемое на объединение двух схем исходных отношений-операндов. Именно по этому условию и происходит отбор кортежей из отношений r 1и r 2в результирующее отношение.

Следует отметить, что операция внутреннего соединения может применяться к отношениям с разными схемами отношений. Эти схемы могут быть любыми, но они ни в коем случае не должны пересекаться.

Кортежи исходных отношений-операндов, попавшие в результат операции внутреннего соединения, называются соединимыми кортежами.

Для наглядного иллюстрирования работы операции внутреннего соединения, приведем следующий пример.

Пусть нам даны два отношения r 1( S 1) и r 2( S 2) с различными схемами отношения:

r 1( S 1):

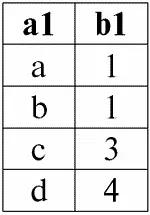
r 2( S 2):

Следующая таблица даст результат применения операции внутреннего соединения по условию P = (b1 = b2).

r 1( S 1) × P r 2( S 2):

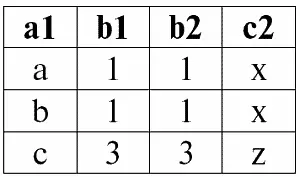
Итак, мы видим, что действительно «слипание» двух таблиц, представляющих отношения, произошло именно по тем кортежам, в которых выполняется условие операции внутреннего соединения P = (b1 = b2).

Теперь на основании уже введенной операции внутреннего соединения мы можем ввести операцию левого внешнего соединенияи правого внешнего соединения. Поясним.

Результатом операции левое внешнее соединение является результат внутреннего соединения, пополненный несоединимыми кортежами левого исходного отношения-операнда. Аналогично результат операции правого внешнего соединения определяется как результат операции внутреннего соединения, пополненный несоединимыми кортежами стоящего справа исходного отношения-операнда.

Вопрос, чем же пополняются результирующие отношения операций левого и правого внешнего соединения, вполне ожидаем. Кортежи одного отношения-операнда дополняются на схеме другого отношения-операнда Null-значениями.

Стоит заметить, что введенные таким образом операции левого и правого внешнего соединения являются производными операциями от операции внутреннего соединения.

Чтобы записать общие формулы для операций левого и правого внешнего соединений, проведем некоторые дополнительные построения.

Пусть нам даны два отношения r 1( S 1) и r 2( S 2) с различными схемами отношений S 1и S 2, не пересекающимися друг с другом.

Так как мы уже оговаривали, что операции левого и правого внутреннего соединения являются производными, то мы можем получить следующие вспомогательные формулы для определения операции левого внешнего соединения:

1) r 3( S 2 ∪ S 1) ≔ r 1( S 1) × P r 2( S 2) ;

r 3( S 2 ∪ S 1) — это просто результат внутреннего соединения отношений r 1( S 1) и r 2( S 2) . Левое внешнее соединение является производной операцией именно от операции внутреннего соединения, поэтому мы и начинаем наши построения с нее;

2) r 4( S 1) ≔ r 3( S 2 ∪ S 1) [ S 1] ;

Таким образом, с помощью унарной операции проекции, мы выделили все соединимые кортежи левого исходного отношения-операнда r 1( S 1) . Результат обозначили r 4( S 1) для удобства применения;