Коллектив Авторов - Базы данных: конспект лекций

И снова рассмотрим действие этой операции над отношениями, представленными в виде таблиц:

r 1( S ):

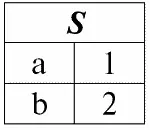
r 2( S ):

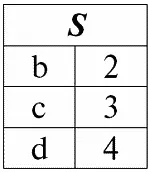
Согласно определению операции пересечением отношений r 1( S ) и r 2( S ) будет новое отношение r 4( S ) , табличное представление которого будет выглядеть следующим образом:

r 4( S ) = r 1( S ) ∩ r 2( S ):

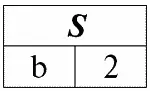
Действительно, если посмотреть на кортежи первого и второго исходного отношений, общий среди них только один: {b, 2}. Он и стал единственным кортежем нового отношения r 4( S ) .

3. Операция разностидвух отношений определяется аналогичным с предыдущими операциями образом. Отношения-операнды, так же, как и в предыдущих операциях, должны иметь одинаковые схемы отношения, тогда в результирующее отношение войдут все те кортежи первого отношения, которых нет во втором, т. е.:

r 5(S) = r 1(S) \ r 2(S) = {t(S) | t ∈ r 1& t ∉ r 2};

Уже хорошо знакомые нам отношения r 1( S ) и r 2( S ) , в табличном представлении выглядящие следующим образом:

r 1( S ):

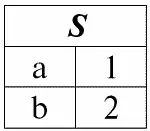
r 2( S ):

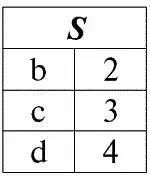
Мы рассмотрим как операнды в операции пересечения двух отношений. Тогда, следуя данному определению, результирующее отношение r5 ( S ) будет выглядеть следующим образом:

r 5( S ) = r 1( S ) \ r 2( S ):

Рассмотренные бинарные операции являются базовыми, на них основываются другие операции, более сложные.

Операция декартового произведения и операция естественного соединения являются бинарными операциями типа произведения и основываются на операции объединения двух отношений, которую мы рассматривали ранее.

Хотя действие операции декартова произведения многим может показаться знакомым, начнем мы все-таки с операции естественного произведения, так как она является более общим случаем, нежели первая операция.

Итак, рассмотрим операцию естественного соединения. Следует сразу заметить, что операндами этого действия могут являться отношения с разными схемами в отличие от трех бинарных операций объединения, пересечения и переименования.

Если рассмотреть два отношения с различными схемами отношений r 1( S 1) и r 2( S 2 ), то их естественным соединениембудет новое отношение r 3( S 3), которое будет состоять только из тех кортежей операндов, которые совпадают на пересечении схем отношений. Соответственно, схема нового отношения будет больше любой из схем отношений исходных, так как является их соединением, «склеиванием». Кстати, кортежи, одинаковые в двух отношениях-операндах, по которым и происходит это «склеивание», называются соединимыми.

Запишем определение операции естественного соединения на языке формул систем управления базами данных:

r 3( S 3) = r 1( S 1) × r 2( S 2) = { t ( S 1∪ S 2) | t [ S 1] ∈ r 1 & t ( S 2) ∈ r 2};

Рассмотрим пример, хорошо иллюстрирующий работу естественного соединения, его «склеивание». Пусть дано два отношения r 1( S 1) и r 2( S 2), в табличной форме представления соответственно равные:

r 1( S 1):

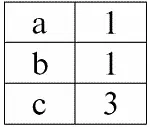
r 2( S 2):

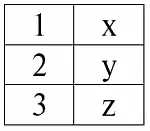
Мы видим, что у этих отношений присутствуют кортежи, совпадающие при пересечении схем S 1и S 2отношений. Перечислим их:

1) кортеж {a, 1} отношения r 1( S 1) совпадает с кортежем {1, x} отношения r 2( S 2);

2) кортеж {b, 1} из r 1( S 1) также совпадает с кортежем {1, x} из r 2( S 2);

3) кортеж {c, 3} совпадает с кортежем {3, z}.

Значит, при естественном соединении новое отношение r 3( S 3) получается «склеиванием» именно на этих кортежах. Таким образом, r 3( S 3) в табличном представлении будет выглядеть следующим образом:

r 3( S 3) = r 1( S 1) × r 2( S 2):

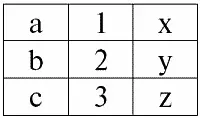
Получается по определению: схема S 3не совпадает ни со схемой S 1, ни со схемой S 2, мы «склеили» две исходные схемы по пересекающимся кортежам, чтобы получить их естественное соединение.

Покажем схематично, как происходит соединение кортежей при применении операции естественного соединения.

Пусть отношение r 1имеет условный вид:

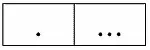
А отношение r 2– вид:

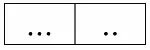
Тогда их естественное соединение будет выглядеть следующим образом:

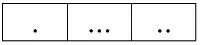
Видим, что «склеивание» отношений-операндов происходит по той самой схеме, что мы приводили ранее, рассматривая пример.

Операция декартового соединенияявляется частным случаем операции естественного соединения. Если конкретнее, то, рассматривая действие операции декартового произведения на отношения, мы заведомо оговариваем, что в этом случае может идти речь только о непересекающихся схемах отношений. В результате применения обеих операций получаются отношения со схемами, равными объединению схем отношений-операндов, только в декартово произведение двух отношений попадают всевозможные пары их кортежей, так как схемы операндов ни в коем случае не должны пересекаться.