Коллектив Авторов - Базы данных: конспект лекций

Именованное значение кортежа на атрибуте(обозначается t(a))определяется по аналогии с атрибутом как упорядоченная пара, состоящая из имени атрибута и значения атрибута, т. е.:

t(a) = (name(a) : x), x ∈ dom(a);

Видим, что значение атрибута берется из домена атрибута.

В табличной форме представления отношения каждое именованное значение кортежа на атрибуте – это соответствующая ячейка таблицы:

Здесь t(a 1), t(a 2), t(a 3) – именованные значения кортежа t на атрибутах а 1, а 2, а 3.

Простейшие примеры именованных значений кортежей на атрибутах:

(Курс: 5), (Балл: 5);

Здесь соответственно Курс и Балл – имена двух атрибутов, а 5 – это одно из их значений, взятое из их доменов. Разумеется, хоть эти значения в обоих случаях равны друг другу, семантически они различны, так как множества этих значений в обоих случаях отличаются друг от друга.

Понятие кортежа в системах управления базами данных может быть интуитивно найдено уже из предыдущего пункта, когда мы говорили об именованном значении кортежа на различных атрибутах. Итак, кортеж(обозначается t, от англ. tuple – «кортеж») со схемой отношения S определяется как множество именованных значений этого кортежа на всех атрибутах, входящих в данную схему отношений S. Другими словами, атрибуты берутся из области определения кортежа, def(t), т. е.:

t ≡ t ( S ) = { t ( a ) | a ∈ def ( t ) ⊆ S ;.

Важно, что одному имени атрибута обязательно должно соответствовать не более одного значения атрибута.

В табличной форме записи отношения кортежем будет любая строка таблицы, т. е.:

Здесь t 1(S) = {t(a 1), t(a 2), t(a 3), t(a 4)} и t 2(S) = {t(a 5), t(a 6), t(a 7), t(a 8)} – кортежи.

Кортежи в СУБД различаются по типамв зависимости от своей области определения. Кортежи называются:

1) частичными,если их область определения включается или совпадает со схемой отношения, т. е. def(t) ⊆ S.

Это общий случай в практике баз данных;

2) полными,в том случае если их область определения полностью совпадает, равна схеме отношения, т. е. def(t) = S;

3) неполными,если область определения полностью включается в схему отношений, т. е. def(t) ⊂ S;

4) нигде не определенными,если их область определения равна пустому множеству, т. е. def(t) = ∅.

Поясним на примере. Пусть у нас имеется отношение, заданное следующей таблицей.

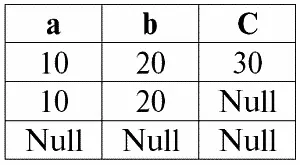
Пусть здесь t 1= {10, 20, 30}, t 2= {10, 20, Null}, t 3= {Null, Null, Null}. Тогда легко заметить, что кортеж t 1– полный, так как его область определения def(t 1) = { a, b, c} = S.

Кортеж t 2– неполный, def(t 2) = { a, b} ⊂ S. И, наконец, кортеж t 3– нигде не определенный, так как его def(t3) = ∅.

Надо заметить, что нигде не определенный кортеж – это пустое множество, тем не менее ассоциируемое со схемой отношений. Иногда нигде не определенный кортеж обозначается: ∅(S). Как мы уже видели в приведенном примере, такой кортеж представляет собой строку таблицы, состоящую только из Null-значений.

Интересно, что сравнимыми, т. е. возможно равными, являются только кортежи с одной и той же схемой отношений. Поэтому, например, два нигде не определенных кортежа с различными схемами отношений не будут равными, как могло ожидаться. Они будут различными так же, как их схемы отношений.

И наконец дадим определение отношению, как некой вершине пирамиды, состоящей из всех предыдущих понятий. Итак, отношение(обозначается r, от англ. relation – «отношение») со схемой отношений S определяется как обязательно конечное множество кортежей, имеющих ту же схему отношения S. Таким образом:

r ≡ r(S) = {t(S) | t ∈r};

По аналогии со схемами отношений количество кортежей в отношении называют мощностью отношенийи обозначают как мощность множества: | r|.

Отношения, как и кортежи, различаются по типам. Итак, отношения называются:

1) частичными, если для любого входящего в отношение кортежа выполняется следующее условие: [def(t) ⊆ S].

Это (как и с кортежами) общий случай;

2) полными, в том случае если ∀t ∈ r(S) выполняется: [def(t) = S];

3) неполными, если ∃t ∈ r(S) def(t) ⊂ S;

4) нигде не определенными, если ∀t ∈ r(S) [def(t) = ∅].

Обратим отдельное внимание на нигде не определенные отношения. В отличие от кортежей работа с такими отношениями включает в себя небольшую тонкость. Дело в том, что нигде не определенные отношения могут быть двух видов: они могут быть либо пустыми, либо могут содержать единственный нигде не определенный кортеж (такие отношения обозначаются {∅(S)}).

Сравнимыми(по аналогии с кортежами), т. е., возможно равными, являются лишь отношения с одной и той же схемой отношения. Поэтому отношения с различными схемами отношений являются различными.

В табличной форме представления, отношение – это тело таблицы, которому соответствует строка – заголовок столбцов, т. е. буквально – вся таблица, вместе с первой строкой, содержащей заголовки.

Реляционная алгебра,как нетрудно догадаться, – это особая разновидность алгебры, в которой все операции производятся над реляционными моделями данных, т. е. над отношениями.

В табличных терминах отношение включает в себя строки, столбцы и строку – заголовок столбцов. Поэтому естественными унарными операциями являются операции выбора определенных строк или столбцов, а также смены заголовков столбцов – переименования атрибутов.

Первой унарной операцией, которую мы рассмотрим, является операция выборки– операция выбора строк из таблицы, представляющей отношение, по какому-либо принципу, т. е. выбор строк-кортежей, удовлетворяющих определенному условию или условиям.

Оператор выборкиобозначается σ < P >, условие выборки– P < S >, т. е., оператор σ берется всегда с определенным условием на кортежи P , а само условие P записывается зависящим от схемы отношения S . С учетом всего этого сама операция выборкинад схемой отношения S применительно к отношению r будет выглядеть следующим образом:

σ < P > r ( S ) ≡ σ < P > r = { t ( S ) | t ∈ r & P < S > t } = { t ( S ) | t ∈ r & IfNull ( P < S > t , False };