Коллектив Авторов - Базы данных: конспект лекций

t 0( S ) ∈ r ( S ) : {(№ зачетной книжки: 100), (Фамилия: ‘Иванов’), (Предмет: ‘Базы данных’), (Оценка: 5)};

Применим оператор переименования к этому кортежу:

ρ<���φ> t 0( S ) : {(№ ЗК: 100), (Фамилия: ‘Иванов’), (Предмет: ‘Базы данных’), (Балл: 5)};

Итак, это один из кортежей нашего отношения, у которого переименовали атрибуты.

В табличных терминах отношение

ρ < № зачетной книжки, Оценка →«№ ЗК, Балл > Сессия —

это новая таблица, полученная из таблицы отношения «Сессия», переименованием указанных атрибутов.

У унарных операций, как и у любых других, есть определенные свойства. Рассмотрим наиболее важные из них.

Первым свойством унарных операций выборки, проекции и переименования является свойство, характеризующее соотношение мощностей отношений. (Напомним, что мощность – это количество кортежей в том или ином отношении.) Понятно, что здесь рассматривается соответственно отношение исходное и отношение, полученное в результате применения той или иной операции.

Заметим, что все свойства унарных операций следуют непосредственно из их определений, поэтому их можно легко объяснить и даже при желании вывести самостоятельно.

Итак:

1) соотношение мощностей:

а) для операции выборки: | σ < P > r |≤ | r |;

б) для операции проекции: | r [ S' ] | ≤ | r |;

в) для операции переименования: | ρ < φ > r | = | r |;

Итого, мы видим, что для двух операторов, а именно для оператора выборки и оператора проекции, мощность исходных отношений – операндов больше, чем мощность отношений, получаемых из исходных применением соответствующих операций. Это происходит потому, что при выборе, сопутствующему действию этих двух операций выборки и проекции, происходит исключение некоторых строк или столбцов, не удовлетворивших условиям выбора. В том случае, когда условиям удовлетворяют все строки или столбцы, уменьшения мощности (т. е. количества кортежей) не происходит, поэтому в формулах неравенство нестрогое.

В случае же операции переименования, мощность отношения не изменяется, за счет того, что при смене имен никакие кортежи из отношения не исключаются;

2) свойство идемпотентности:

а) для операции выборки: σ < P > σ < P > r = σ < P >;

б) для операции проекции: r [ S’ ] [ S’ ] = r [ S' ];

в) для операции переименования в общем случае свойство идемпотентности неприменимо.

Это свойство означает, что двойное последовательное применение одного и того же оператора к какому-либо отношению равносильно его однократному применению.

Для операции переименования атрибутов отношения, вообще говоря, это свойство может быть применено, но обязательно со специальными оговорками и условиями.

Свойство идемпотентности очень часто используется для упрощения вида выражения и приведения его к более экономичному, актуальному виду.

И последнее свойство, которое мы рассмотрим, – это свойство монотонности. Интересно заметить, что при любых условиях все три оператора монотонны;

3) свойство монотонности:

а) для операции выборки: r 1 ⊆ r 2⇒ σ < P > r 1 ⇒ σ < P > r 2;

б) для операции проекции: r 1 ⊆ r 2 ⇒ r 1[ S' ] ⊆ r 2[ S' ];

в) для операции переименования: r 1 ⊆ r 2 ⇒ ρ < φ > r 1⊆ ρ < φ > r 2;

Понятие монотонности в реляционной алгебре аналогично этому же понятию из алгебры обычной, общей. Поясним: если изначально отношения r 1и r 2были связаны между собой таким образом, что r ⊆ r 2 , то и после применения любого их трех операторов выборки, проекции или переименования это соотношение сохранится.

У любых операций есть свои правила применимости, которые необходимо соблюдать, чтобы выражения и действия не теряли смысла. Бинарные теоретико-множественные операции объединения, пересечений и разности могут быть применены только к двум отношениям обязательно с одной и той же схемой отношения. Результатом таких бинарных операций будут являться отношения, состоящие из кортежей, удовлетворяющих условиям операций, но с такой же схемой отношения, как и у операндов.

1.Результатом операции объединениядвух отношений r 1( S ) и r 2( S ) будет новое отношение r 3( S ), состоящее из тех кортежей отношений r 1( S ) и r 2( S ), которые принадлежат хотя бы одному из исходных отношений и с такой же схемой отношения.

Таким образом, пересечение двух отношений – это:

r 3( S ) = r 1( S ) ∪ r 2( S ) = { t ( S ) | t ∈ r 1∪ t ∈ r 2} ;

Для наглядности, приведем пример в терминах таблиц:

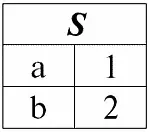
Пусть даны два отношения:

r 1( S ):

r 2( S ):

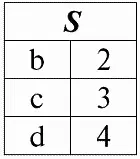
Мы видим, что схемы первого и второго отношений одинаковы, только имеют различной количество кортежей. Объединением этих двух отношений будет отношение r 3( S ) , которому будет соответствовать следующая таблица:

r3 ( S ) = r 1( S ) ∪ r 2( S ):

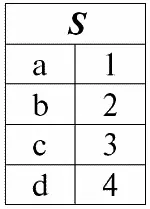
Итак, схема отношения S не изменилась, только выросло количество кортежей.

2. Перейдем к рассмотрению следующей бинарной операции – операции пересечениядвух отношений. Как мы знаем еще из школьной геометрии, в результирующее отношение войдут только те кортежи исходных отношений, которые присутствуют одновременно в обоих отношениях r 1( S ) и r 2( S ) (снова обращаем внимание на одинаковую схему отношения).

Операция пересечения двух отношений будет выглядеть следующим образом:

r 4( S ) = r 1( S ) ∩ r 2( S ) = { t ( S ) | t ∈ r 1& t ∈ r 2};