Коллектив Авторов - Базы данных: конспект лекций

Таким образом, исходя из всего вышесказанного запишем математическую формулу для операции декартового произведения:

r 4( S 4) = r 1( S1 ) × r 2( S 2) = { t ( S 1 ∪ S 2) | t [ S 1] ∈ r 1& t ( S 2) ∈ r 2}, S 1∩ S 2= ∅;

Теперь рассмотрим пример, чтобы показать, какой вид будет иметь результирующая схема отношения, при применении операции декартового произведения.

Пусть даны два отношения r 1( S1 ) и r 2( S 2) , которые в табличном виде представляются следующим образом:

r 1( S 1):

r 2( S 2):

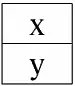
Итак, мы видим, что ни один из кортежей отношений r 1( S 1) и r 2( S 2) , действительно, не совпадает в их пересечении. Поэтому в результирующее отношение r 4( S 4) попадут всевозможные пары кортежей первого и второго отношений-операндов. Получится:

r 4( S 4) = r 1( S1 ) × r 2( S 2):

Получилась новая схема отношения r 4( S 4) не «склеиванием» кортежей как в предыдущем случае, а перебором всех возможных различных пар несовпадающих в пересечении исходных схем кортежей.

Снова, как и в случае естественного соединения, приведем схематичный пример работы операции декартового произведения.

Пусть r 1задано следующим условным образом:

А отношение r 2задано:

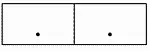
Тогда их декартовое произведение схематично можно изобразить следующим образом:

Именно таким образом и получается результирующее отношение при применении операции декартового произведения.

Из приведенных выше определений бинарных операций объединения, пересечения, разности, декартового произведения и естественного соединения следуют свойства.

1. Первое свойство, как и в случае унарных операций, иллюстрирует соотношение мощностейотношений:

1) для операции объединения:

| r 1 ∪ r 2| ≤| r 1| + | r 2|;

2) для операции пересечения:

| r 1∩ r 2| ≤ min (| r 1|, | r 2|);

3) для операции разности:

| r 1\ r 2| ≤ | r 1|;

4) для операции декартового произведения:

| r 1× r 2| = | r 1| · | r 2|;

5) для операции естественного соединения:

| r 1× r 2| ≤ | r 1| · | r 2|.

Соотношение мощностей, как мы помним, характеризует, как меняется количество кортежей в отношениях после применения той или иной операции. Итак, что мы видим? Мощность объединениядвух отношений r 1и r 2меньше суммы мощностей исходных отношений-операндов. Почему это происходит? Все дело в том, что при объединении совпадающие кортежи исчезают, накладываясь друг на друга. Так, обратившись к примеру, который мы рассматривали по прохождении этой операции, можно заметить, что в первом отношении было два кортежа, во втором – три, а в результирующем – четыре, т. е. меньше, чем пять (сумма мощностей отношений-операндов). По совпадающему кортежу {b, 2} эти отношения «склеились».

Мощность результата пересечениядвух отношений меньше или равна минимальной мощности исходных отношений-операндов. Обратимся к определению этой операции: в результирующее отношение попадают только те кортежи, которые присутствуют в обоих отношениях исходных. А значит, мощность нового отношения никак не может превышать мощности того отношения-операнда, число кортежей которого наименьшее из двух. А равной этой минимальной мощности мощность результата быть может, так как всегда допускается случай, когда все кортежи отношения с меньшей мощностью совпадают с какими-то кортежами второго отношения-операнда.

В случае операции разностивсе достаточно тривиально. Действительно, если из первого отношения-операнда «вычесть» все кортежи, присутствующие также во втором отношении, то их количество (а следовательно, мощность) уменьшится. В том случае, если ни один кортеж первого отношения не совпадет ни с одним кортежем отношения второго, т. е. «вычитать» будет нечего, мощность его не уменьшится.

Интересно, что в случае применения операции декартового произведениямощность результирующего отношения в точности равна произведению мощностей двух отношений-операндов. Понятно, что это происходит потому, что в результат записываются все возможные пары кортежей исходных отношений, а ничего не исключается.

И, наконец, операцией естественного соединенияполучается отношение, мощность которого больше или равна произведения мощностей двух исходных отношений. Опять-таки это происходит потому, что отношения-операнды «склеиваются» по совпадающим кортежам, а несовпадающие – из результата исключаются вовсе.

2. Свойство идемпотентности:

1) для операции объединения: r ∪ r = r ;

2) для операции пересечения: r ∩ r = r ;

3) для операции разности: r \ r ≠ r ;

4) для операции декартового произведения (в общем случае, свойство не применимо);

5) для операции естественного соединения: r × r = r .

Интересно, что свойство идемпотентности верно не для всех операций из приведенных, а для операции декартового произведения оно и вовсе не применимо. Действительно, если объединить, пересечь или естественно соединить какое-либо отношение само с собой, оно не изменится. А вот если отнять от отношения точно равное ему отношение, в результате получится пустое отношение.

3. Свойство коммутативности:

1) для операции объединения:

r 1∪ r 2= r 2∪ r 1;

2) для операции пересечения:

r ∩ r = r ∩ r ;

3) для операции разности:

r 1\ r 2≠ r 2\ r 1;

4) для операции декартового произведения:

r 1× r 2= r 2× r 1;

5) для операции естественного соединения: