Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

• нужно, чтобы операции вставки и удаления выполнялись чрезвычайно быстро;

• не требуется произвольный доступ к данным;

• приходится вставлять или удалять элементы между других элементов;

• заранее не известно количество элементов (оно будет расти или уменьшится по ходу выполнения программы).

Массивы предпочтительнее связных списков, когда:

• нужен произвольный доступ к данным;

• нужен очень быстрый доступ к элементам;

• число элементов не изменяется во время выполнения программы, благодаря чему легко выделить непрерывное пространство памяти.

Как и связный список, дерево (tree) использует элементы, которым для хранения объектов не нужно располагаться в физической памяти непрерывно. Ячейки здесь тоже имеют указатели на другие ячейки, однако, в отличие от связных списков, они располагаются не линейно, а в виде ветвящейся структуры. Деревья особенно удобны для иерархических данных, таких как каталоги с файлами или система субординации (рис. 4.5).

В терминологии деревьев ячейка называется узлом , а указатель из одной ячейки на другую — ребром . Самая первая ячейка — это корневой узел , он единственный не имеет родителя. Все остальные узлы в деревьях должны иметь строго одного родителя [47] Если узел нарушает это правило, многие алгоритмы поиска по дереву не будут работать. .

Два узла с общим родителем называются братскими. Родитель узла, прародитель, прапрародитель (и т. д. вплоть до корневого узла) — это предки. Аналогично дочерние узлы, внуки, правнуки (и т. д. вплоть до нижней части дерева) называются потомками.

Узлы, не имеющие дочерних узлов, — это листья (по аналогии с листьями настоящего дерева ). Путь между двумя узлами определяется множеством узлов и ребер.

Уровень узла — это длина пути от него до корневого узла, высота дерева — уровень самого глубокого узла в дереве (рис. 4.6). И, наконец, множество деревьев называется лесом .

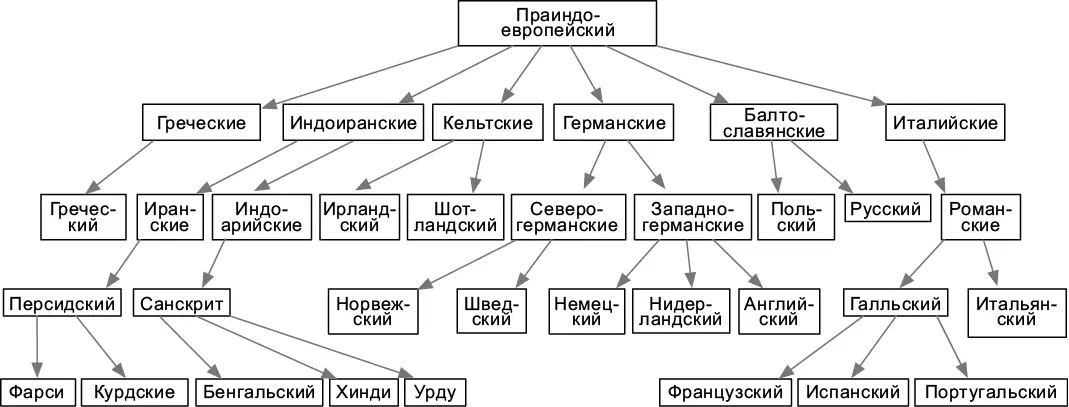
Рис. 4.5.Дерево происхождения индоевропейских языков

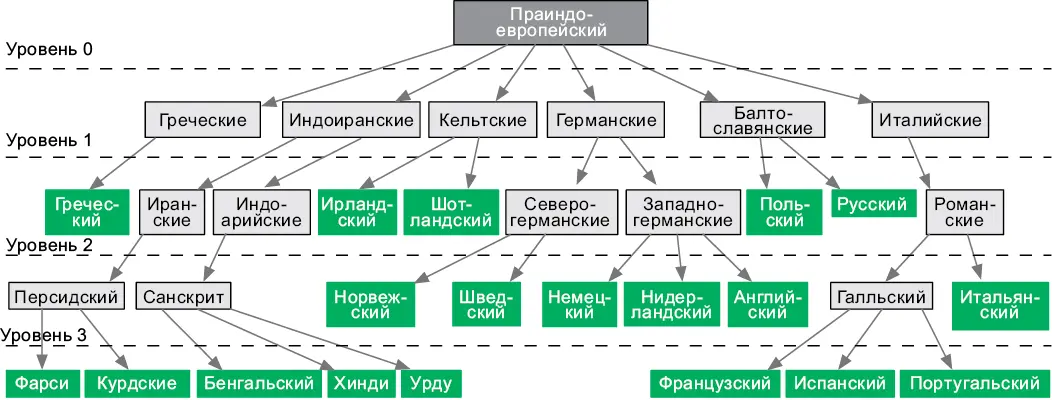
Рис. 4.6.Листья этого дерева представляют современные языки

Двоичное дерево поиска (binary search tree) — это особый тип дерева, поиск в котором выполняется особенно эффективно. Узлы в двоичном дереве поиска могут иметь не более двух дочерних узлов. Кроме того, узлы располагаются согласно их значению/ключу. Дочерние узлы слева от родителя должны быть меньше него, а справа — больше (рис. 4.7).

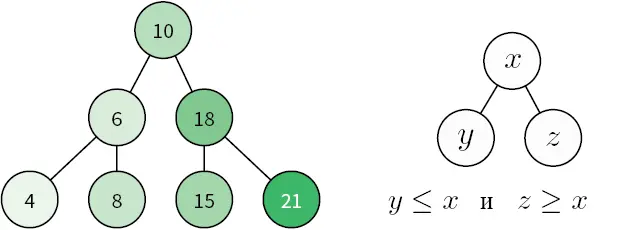
Рис. 4.7.Пример двоичного дерева поиска

Если дерево соблюдает это свойство, в нем легко отыскать узел с заданным ключом/значением:

function find_node(binary_tree, value)

node ← binary_tree.root_node

····while node

········if node.value = value

············return node

········if value > node.value

············node ← node.right

········else

············node ← node.left

····return "NOT FOUND"

Чтобы вставить элемент, находим последний узел, следуя правилам построения дерева поиска, и подключаем к нему новый узел справа или слева:

function insert_node(binary_tree, new_node)

····node ← binary_tree.root_node

····while node

········last_node ← node

········if new_node.value > node.value

············node ← node.right

········else

············node ← node.left

····if new_node.value > last_node.value

········last_node.right ← new_node

····else

········last_node.left ← new_node

Балансировка дерева.Если вставить в двоичное дерево поиска слишком много узлов, в итоге получится очень высокое дерево, где большинство узлов имеют всего один дочерний узел. Например, если последовательно вставлять узлы с ключами/значениями, которые всегда больше предыдущих, в итоге получится нечто, похожее на связный список. Однако мы можем перестроить узлы в дереве так, что его высота уменьшится. Эта процедура вызывается балансировкой дерева . Идеально сбалансированное дерево имеет минимальную высоту (рис. 4.8).

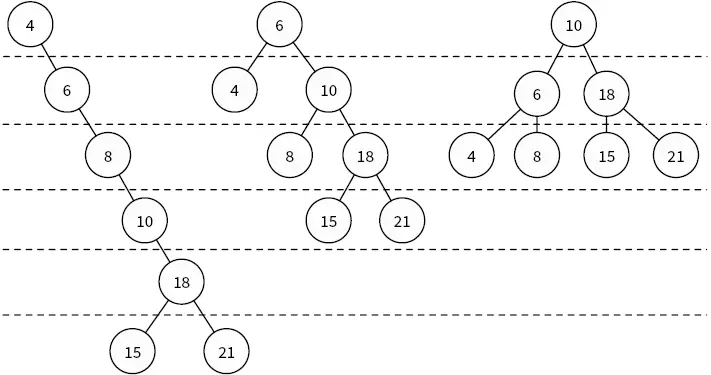
Рис. 4.8.Одно и то же двоичное дерево поиска с разной балансировкой: сбалансированное плохо, средне и идеально

Большинство операций с деревом требует обхода узлов по ссылкам, пока не будет найден конкретный узел. Чем больше высота дерева, тем длиннее средний путь между узлами и тем чаще приходится обращаться к памяти. Поэтому важно уменьшать высоту деревьев. Идеально сбалансированное двоичное дерево поиска можно создать из сортированного списка узлов следующим образом:

function build_balanced(nodes)

····if nodes is empty

········return NULL

····middle ← nodes.length/2

····left ← nodes.slice(0, middle — 1)

····right ← nodes.slice(middle + 1, nodes.length)

····balanced ← BinaryTree.new(root=nodes[middle])

····balanced.left ← build_balanced(left)

····balanced.right ← build_balanced(right)

····return balanced

Рассмотрим двоичное дерево поиска с n узлами и с максимально возможной высотой n . В этом случае оно похоже на связный список. Минимальная высота идеально сбалансированного дерева равняется log 2 n . Сложность поиска элемента в дереве пропорциональна его высоте. В худшем случае, чтобы найти элемент, придется опускаться до самого нижнего уровня листьев. Поиск в сбалансированном дереве с n элементами, следовательно, имеет O (log n ). Вот почему эта структура данных часто выбирается для реализации множеств (где предполагается проверка присутствия элементов) и словарей (где нужно искать пары «ключ — значение»).

Однако балансировка дерева — дорогостоящая операция, поскольку требует сортировки всех узлов. Если делать балансировку после каждой вставки или удаления, операции станут значительно медленнее. Обычно деревья подвергаются этой процедуре после нескольких вставок и удалений. Но балансировка от случая к случаю является разумной стратегией только в отношении редко изменяемых деревьев.

Для эффективной обработки двоичных деревьев, которые изменяются часто, были придуманы сбалансированные двоичные деревья (self-balancing binary tree) [48] Иногда их называют двоичными деревьями с автоматической балансировкой, или самоуравновешивающимися двоичными деревьями. — Примеч. пер. . Их процедуры вставки или удаления элементов гарантируют, что дерево остается сбалансированным. Красно-черное дерево (red-black tree) — это хорошо известный пример сбалансированного дерева, которое окрашивает узлы красным либо черным цветом в зависимости от стратегии балансировки [49] Стратегии автоматической балансировки выходят за рамки этой книги. Если вам любопытно, то в Интернете имеются видеоматериалы, которые показывают, как работают эти алгоритмы. . Красно-черные деревья часто используются для реализации словарей: словарь может подвергаться интенсивной правке, но конкретные ключи в нем по-прежнему будут находиться быстро вследствие балансировки.