Владстон Феррейра Фило - Теоретический минимум по Computer Science [Все что нужно программисту и разработчику]

эффективно сортируют очень длинные списки;

быстро отыскивают нужный элемент;

оперируют и управляют графами ;

используют исследование операций для оптимизации процессов.

Вы научитесь распознавать проблемы, к которым можно применить известные решения. Существует много различных типов задач: сортировка данных, поиск закономерностей (образов, шаблонов), прокладывание маршрута и др. И многие типы алгоритмов имеют непосредственное отношение к областям научно-практических исследований: обработке изображений, криптографии, искусственному интеллекту… В этой книге мы не сможем охватить их все [52] Вот более полный список: https://code.energy/algo-list . . Однако мы изучим самые важные алгоритмы, с которыми должен быть знаком любой хороший программист.

До появления компьютеров сортировка данных была известной проблемой, ее ручное выполнение занимало колоссальное количество времени. Когда в 1890-х годах компания Tabulating Machine Company (которая позже стала называться IBM) автоматизировала операции сортировки, это позволило на несколько лет быстрее обработать данные переписи населения США.

Существует много алгоритмов сортировки. Более простые имеют временную сложность O ( n 2). Сортировка выбором (см. раздел «Оценка затрат времени» главы 2) — один из таких алгоритмов. Именно его люди предпочитают использовать для сортировки физической колоды карт. Сортировка выбором принадлежит многочисленной группе алгоритмов с квадратичной стоимостью. Мы, как правило, используем их для упорядочивания наборов данных, состоящих меньше чем из 1000 элементов. Одним из известных алгоритмов является сортировка вставками . Он показывает очень хорошую эффективность в сортировке уже почти упорядоченных наборов данных даже очень большого объема:

function insertion_sort(list)

····for i ← 2 … list.length

········j ← i

········while j and list[j-1] > list[j]

············list.swap_items(j, j-1)

············j ← j — 1

Выполните этот алгоритм на бумаге, с использованием большей частью отсортированного списка чисел. Для массивов, где не упорядочено незначительное число элементов, insertion_sort имеет сложность O ( n ). В этом случае он выполняет меньше операций, чем какой-либо другой алгоритм сортировки.

В отношении крупных наборов данных, о которых нельзя сказать, что они отсортированы большей частью, алгоритмы с временной сложностью O ( n 2) оказываются слишком медленными (см. табл. 3.2). Здесь нам нужны более эффективные подходы. Самыми известными высокоскоростными алгоритмами сортировки являются сортировка слиянием (см. раздел «Разделяй и властвуй» главы 3) и так называемая быстрая сортировка , оба имеют сложность O ( n log n ). Вот как алгоритм быстрой сортировки раскладывает по порядку колоду карт.

1. Если в колоде менее четырех карт, то упорядочить их — и работа завершена. В противном случае перейти к шагу 2.

2. Вынуть из колоды наугад любую карту, которая становится опорной .

3. Карты со значением больше , чем у опорной, кладутся в новую колоду справа ; карты с меньшим значением кладутся в новую колоду слева .

4. Проделать эту процедуру для каждой из двух только что созданных колод.

5. Объединить левую колоду, опорную карту и правую колоду, чтобы получить отсортированную колоду (рис. 5.1).

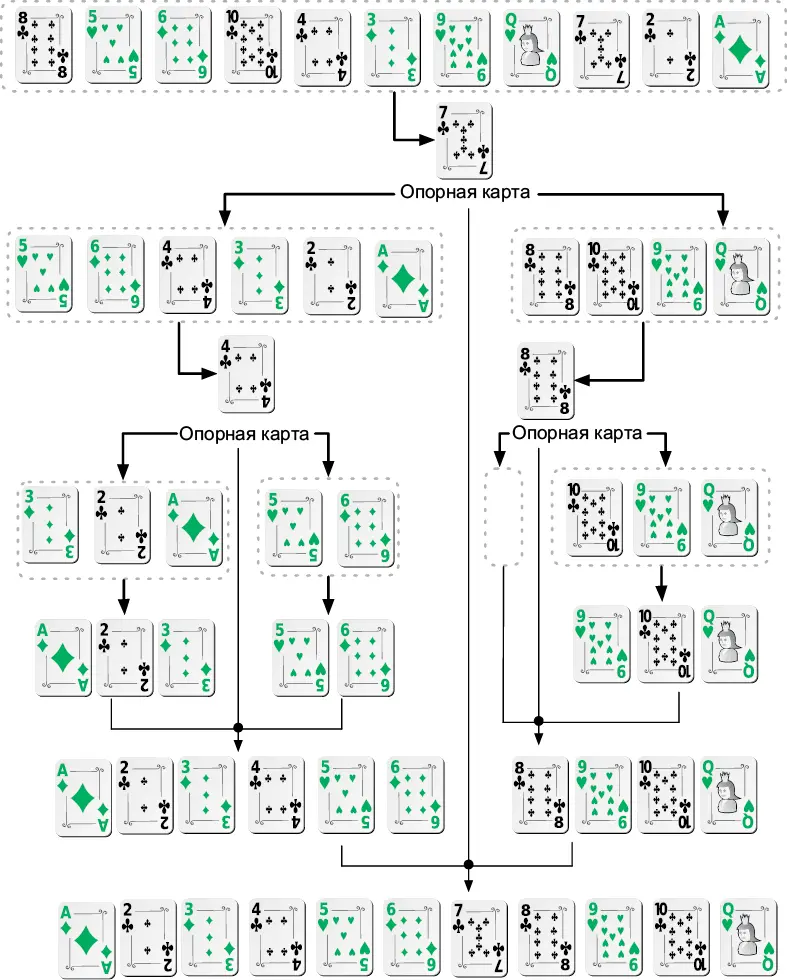
Рис. 5.1.Пример выполнения быстрой сортировки

Перетасуйте колоду карт и проделайте описанные шаги. Это поможет вам опробовать на практике алгоритм быстрой сортировки, а заодно укрепит ваше понимание рекурсии.

Теперь вы готовы решать большинство задач, связанных с сортировкой. Здесь мы осветили не все алгоритмы сортировки, так что просто помните, что их гораздо больше и каждый из них соответствует конкретным задачам.

Поиск определенной информации в памяти является ключевой операцией в вычислениях. Программисту очень важно владеть алгоритмами поиска. Самый простой из них — последовательный поиск : вы просматриваете все элементы один за другим, пока не будет найден нужный; как вариант, вы можете проверить все элементы, чтобы понять, что искомого среди них нет.

Легко заметить, что последовательный поиск имеет сложность O ( n ), где n — это общее количество элементов в пространстве поиска. Но на случай, когда элементы хорошо структурированы, есть более эффективные алгоритмы. В разделе «Структуры» предыдущей главы мы убедились, что извлечение данных, представленных в формате сбалансированного двоичного дерева поиска, стоит всего O (log n ).

Если ваши элементы хранятся в сортированном массиве, то их можно отыскать за такое же время, O (log n ), посредством двоичного поиска . Этот алгоритм на каждом шаге отбрасывает половину пространства поиска:

function binary_search(items, key)

····if not items

········return NULL

····i ← items.length / 2

····if key = items[i]

········return items[i]

····if key > items[i]

········sliced ← items.slice(i+1, items.length)

····else

········sliced ← items.slice(0, i-1)

····return binary_search(sliced, key)

На каждом шаге алгоритм binary_search выполняет постоянное число операций и отбрасывает половину входных данных. Это означает, что для n элементов пространство поиска сведется к нулю за log 2 n шагов. Поскольку на каждом шаге выполняется постоянное количество операций, алгоритм имеет сложность O (log n ). Вы можете выполнять поиск среди миллиона или триллиона элементов, и этот алгоритм по-прежнему будет показывать хорошую производительность.

Впрочем, существуют еще более эффективные алгоритмы. Если элементы хранятся в хеш-таблице (см. раздел «Структуры» предыдущей главы), достаточно вычислить хеш-ключ искомого элемента. Этот хеш даст его адрес! Время, необходимое для нахождения элемента , не меняется с увеличением пространства поиска. Не имеет значения, ищете вы среди миллионов, миллиардов или триллионов элементов, — количество операций останется постоянным, а значит, процесс имеет временную сложность O (1), он действует почти мгновенно.

Мы уже знаем, что графы — гибкая структура данных, которая для хранения информации использует вершины и ребра. Графы широко используются для представления таких данных, как социальные сети (вершины — люди, ребра — дружеские связи), телефонные сети (вершины — телефоны и станции, ребра — линии связи) и многих других.