Роберт Мартин - Чистая архитектура. Искусство разработки программного обеспечения

На рис. 14.5 представлена диаграмма с устойчивым компонентом X. От него зависят три других компонента, то есть имеется три веские причины не изменять его. Мы говорим, что X несет ответственность за эти три компонента. Сам компонент X, напротив, ни от чего не зависит, то есть на него не оказывается никаких внешних воздействий, которые могли бы привести к изменению. Мы говорим, что он независим .

На рис. 14.6 изображен очень неустойчивый компонент Y. От него не зависит никакой другой компонент, поэтому мы говорим, что он лишен ответственности. Имеется также три компонента, от которых зависит Y, поэтому необходимость его изменения может проистекать из трех внешних источников. Мы говорим, что Y зависим.

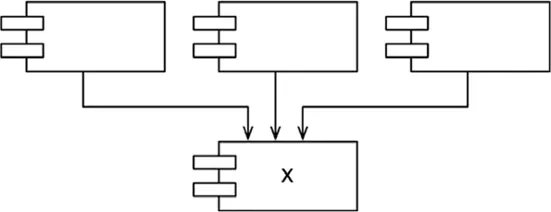
Рис. 14.5.X: устойчивый компонент

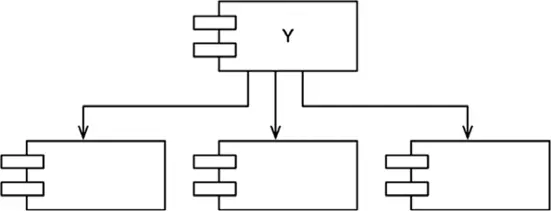
Рис. 14.6.Y: очень неустойчивый компонент

Как оценить устойчивость компонента? Один из способов — подсчитать количество входящих и исходящих зависимостей этого компонента. Эти числа позволят вычислить меру его устойчивости.

• Fan-in ( число входов ): количество входящих зависимостей. Эта метрика определяет количество классов вне данного компонента, которые зависят от классов внутри компонента.

• Fan-out ( число выходов ): количество исходящих зависимостей. Эта метрика определяет количество классов внутри данного компонента, зависящих от классов за его пределами.

• I : неустойчивость: I = Fan-out ÷ ( Fan-in + Fan-out ). Значение этой метрики изменяется в диапазоне [0, 1]. I = 0 соответствует максимальной устойчивости компонента, I = 1 — максимальной неустойчивости.

Метрики Fan-in (число входов) и Fan-out (число выходов) [31] В предыдущих публикациях я использовал для связей имена Efferent (центробежный) и Afferent (центростремительный), Ce и Ca , вместо Fan-out и Fan-in соответственно. Это был всего лишь каприз с моей стороны: мне нравилось сравнение с центральной нервной системой. определяются как количество классов за пределами компонентов, связанных зависимостями с классами внутри компонента. Рассмотрим пример, изображенный на рис. 14.7.

Рис. 14.7.Пример

Рассчитаем устойчивость компонента Cc. Вне компонента Cc имеется три класса, зависящих от классов внутри Cc. То есть Fan-in = 3. Кроме того, вне Cc имеется один класс, от которого зависят классы внутри Cc. То есть Fan-out = 1 и I = 1/4.

В C++ эти зависимости обычно представлены инструкциями #include. В действительности метрику I проще вычислять, когда исходный код организован так, что каждый класс хранится в отдельном файле. В Java метрику I можно вычислить, подсчитав количество инструкций import и полных квалифицированных имен.

Если метрика I равна 1, это означает, что никакой другой компонент не зависит от данного компонента ( Fan-in = 0) и данный компонент зависит от других компонентов ( Fan-out > 0). Это признак неустойчивости компонента; он безответствен и зависим. Отсутствие зависящих компонентов означает, что он не может служить причиной изменения других компонентов, а его собственная зависимость может послужить веским основанием для изменения самого компонента.

Напротив, когда метрика I равна 0, это означает, что от компонента зависят другие компоненты ( Fan-in > 0), но сам он не зависит от других компонентов ( Fan-out = 0). Такой компонент ответствен и независим . Он занимает максимально устойчивое положение. Зависимости от него усложняют изменение компонента, а отсутствие компонентов, от которых он зависит, означает отсутствие сил, которые могли бы заставить его измениться.

Принцип устойчивых зависимостей (SDP) говорит, что метрика I компонента должна быть больше метрик I компонентов, которые от него зависят. То есть метрики I должны уменьшаться в направлении зависимости.

Если все компоненты в системе будут иметь максимальную устойчивость, такую систему невозможно будет изменить. Это нежелательная ситуация. В действительности структура компонентов должна проектироваться так, чтобы в ней имелись и устойчивые, и неустойчивые компоненты. Диаграмма на рис. 14.8 демонстрирует идеальную организацию системы с тремя компонентами.

Изменяемые компоненты находятся вверху и зависят от устойчивого компонента внизу. Размещение неустойчивых компонентов в верхней части диаграммы — общепринятое и очень удобное соглашение, потому что любые стрелки, направленные вверх , ясно покажут нарушение принципа устойчивых зависимостей (и, как вы убедитесь далее, принципа ацикличности зависимостей).

Рис. 14.8.Идеальная организация системы с тремя компонентами

Диаграмма на рис. 14.9 демонстрирует нарушение принципа SDP.

Компонент Flexible специально проектировался так, чтобы его было легко изменять. Предполагалось, что он будет неустойчивым. Но кто-то из разработчиков, работающих над компонентом Stable, создал зависимость от компонента Flexible. Это явное нарушение принципа SDP, потому что

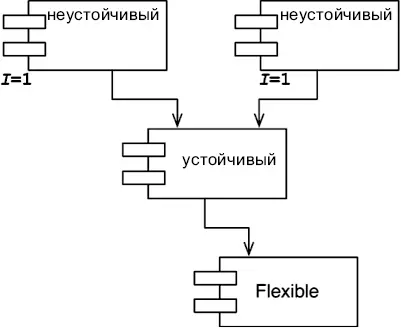
Рис. 14.9.Нарушение принципа SDP

метрика I компонента Stable намного меньше метрики I компонента Flexible. Как результат, создание такой зависимости усложнило возможное изменение компонента Flexible. Теперь любые изменения в компоненте Flexible придется согласовывать с компонентом Stable и всеми компонентами, зависящими от него.

Чтобы исправить проблему, нужно разорвать зависимость Stable от Flexible. Зачем нужна эта зависимость? Допустим, что в компоненте Flexible имеется класс C, который используется другим классом U из компонента Stable (рис. 14.10).

Рис. 14.10.Класс U в компоненте Stable использует класс C в компоненте Flexible

Исправить ситуацию можно, применив принцип инверсии зависимостей (DIP). Для этого определим интерфейс US и поместим его в компонент с именем UServer. Этот интерфейс должен объявлять все методы, используемые классом U. Затем реализуем этот интерфейс в классе C, как показано на рис. 14.11. Это разорвет зависимость Stable от Flexible и вынудит оба компонента зависеть от UServer. UServer очень устойчив ( I = 0), а Flexible сохранит желаемую неустойчивость ( I = 1). Теперь все зависимости простираются в сторону уменьшения I .